Метод контурных токов
Для каждого из взаимно независимых контуров назначается так называемый контурный ток, замыкающийся по всем ветвям контура. Направления этих токов произвольны.
На рис. 1.9 они обозначены дугообразными стрелками, рядом с которыми стоят буквы IK1, IK2, IK3 и IK4. Для выбранных контурных токов записываются уравнения по второму закону Кирхгофа. Контур при этом обходится по направлению контурного тока. Рассмотрим порядок составления уравнения на примере третьего контура. Контурный ток IK3, протекая по сопротивлениям своего контура, создает на них падение напряжения
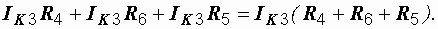 (1.10)
(1.10)
По сопротивлению R4, являющемуся элементом третьего контура, протекает контурный ток IK2. Создаваемое им падение напряжения IK2R4 вычитается из предыдущего, так как направление тока IK2 в сопротивлении R4 противоположно току IK3. Сопротивление R6 также входит в третий контур. Падение напряжения на нем, создаваемое контурным током IK4, складывается с суммой (1.10), так как направления IK4 и IK3 в R6 одинаковы. В правой части уравнения записывается алгебраическая сумма всех ЭДС контура, в данном случае – единственная ЭДС E4.
Итак, для третьего контура имеем:
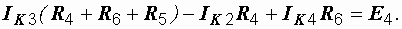
Аналогично составляются и остальные контурные уравнения:
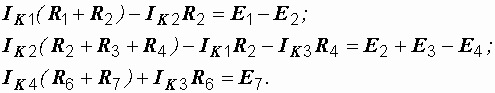
После решения последней системы действительные токи ветвей определяются по найденным контурным:
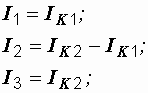
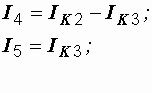
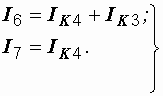 (1.11)
(1.11)
Контурные уравнения получаются подстановкой формул (1.11) в уравнения второго закона Кирхгофа (1.7).
Метод наложения
В основе метода лежит принцип суперпозиции (наложения):ток в любой ветви сложной электрической цепи, содержащей несколько ЭДС, может быть найден как алгебраическая сумма токов в этой ветви от действия каждой ЭДС в отдельности.
Это весьма важное положение, справедливое только для линейных цепей, вытекает из уравнений Кирхгофа и утверждает независимость действия источников энергии. Основанный на нем метод сводит расчет цепи, содержащей несколько ЭДС, к последовательному расчету схем, каждая из которых содержит только один источник.
Например, токи в схеме на рис. 1.10, а находятся как алгебраические суммы частичных токов, определяемых из схем 1.10, б и в.
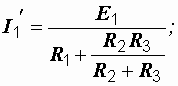
| 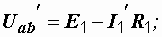
|
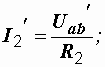
| 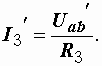
|
Аналогично:
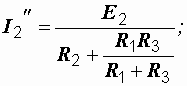
| 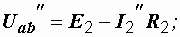
|
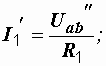
| 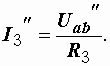
|
И, наконец,
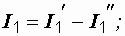
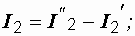
a) б) в)
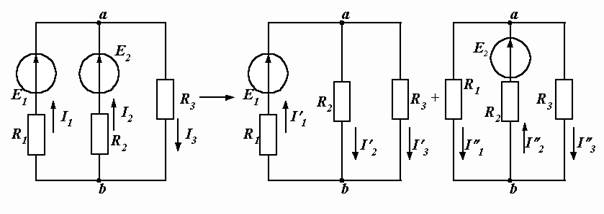
Рис. 1.10. Заданная (а) и расчетные (б и в) схемы
При расчете подобных схем очень удобным оказывается следующий прием. Пусть требуется определить токи в параллельных ветвях при известном суммарном токе (рис. 1.11).
Имеем:
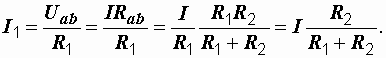
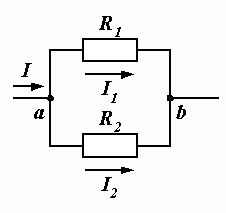 Рис. 1.11. Токи в параллельных ветвях
Рис. 1.11. Токи в параллельных ветвях
| Из полученной формулы вытекает правило:ток в одной из двух параллельных ветвей равен произведению общего тока на сопротивление соседней ветви, деленному на сумму сопротивлений параллельных ветвей.
Пользуясь этим правилом для тока I2 можно написать:
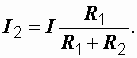
|
Применение этого правила избавляет от необходимости определять напряжения 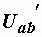 и
и 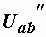 в схемах на рис. 1.10, б и 1.10, в. Так, после определения тока
в схемах на рис. 1.10, б и 1.10, в. Так, после определения тока 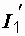 , токи
, токи 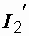 и
и 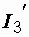 можно найти по формулам:
можно найти по формулам:
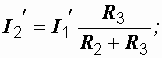
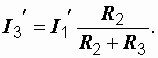
Дата добавления: 2020-10-14; просмотров: 405;











