Рекуррентные методы
При большом объеме совокупности данных наблюдения х конечные методы решения уравнения правдоподобия приводят к значительным вычислительным трудностям, связанным с необходимостью запоминания большого числа исходных данных и промежуточных результатов вычислений. В связи с этим особый интерес представляют рекуррентные методы, в которых оценка максимального правдоподобия вычисляется по шагам с постепенно увеличивающейся точностью, причем каждый шаг связан с получением новых данных наблюдения, а рекуррентная процедура строится так, чтобы хранить в памяти по возможности наименьшее количество данных от предыдущих шагов. Дополнительным и весьма существенным с практической точки зрения преимуществом рекуррентных методов является готовность к выдаче результата на любом промежуточном шаге.
Это обусловливает целесообразность применения рекуррентных методов даже в тех случаях, если удается получить точное решение уравнения максимального правдоподобия конечным методом, и делает их еще более ценными, когда невозможно найти точное аналитическое выражение для оценки максимального правдоподобия.
Пусть совокупность данных наблюдения представляет собой последовательность 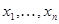 для описания которой введем вектор
для описания которой введем вектор 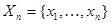 . (Как всегда, каждая его компонента
. (Как всегда, каждая его компонента 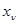 , в свою очередь, может быть вектором, отрезком случайного процесса и т. д.). Пусть
, в свою очередь, может быть вектором, отрезком случайного процесса и т. д.). Пусть 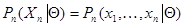 - функция правдоподобия, а
- функция правдоподобия, а
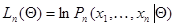 (7.5.15)
(7.5.15)
ее логарифм. Последний всегда можно представить в виде
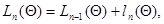 (7.5.16)
(7.5.16)
где
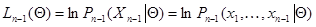 (7.5.17)
(7.5.17)
- логарифм функции правдоподобия для совокупности данных наблюдения 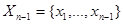 без последнего значения, а
без последнего значения, а
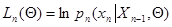 (7.5.18)
(7.5.18)
- логарифм условной плотности вероятности значения 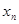 при заданных значениях
при заданных значениях 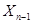 и
и 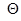 .
.
Представление (7,5.16) для логарифма функции правдоподобия является основой для получения рекуррентной процедуры вычисления оценки максимального правдоподобия. Рассмотрим регулярный случай. При этом оценка максимального правдоподобия может быть найдена как решение уравнения
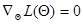 , (7.5.19)
, (7.5.19)
которое отличается от (7.1.6) только введением индекса п у логарифма функции правдоподобия.
Обозначим решение этого уравнения через 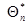 подчеркнув тем самым, что эта оценка получена по совокупности данных наблюдения
подчеркнув тем самым, что эта оценка получена по совокупности данных наблюдения 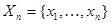 . Аналогично обозначим через
. Аналогично обозначим через 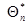 решение уравнения
решение уравнения 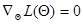 - оценку максимального правдоподобия, полученную по совокупности данных
- оценку максимального правдоподобия, полученную по совокупности данных 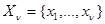 .
.
Уравнение (7.5.19) можно переписать с учетом (7.5.16) в следующем виде:
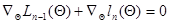 . (7.5.20)
. (7.5.20)
Разложим левую часть (7.5.20) в ряд Тейлора в окрестности точки 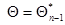 . При этом
. При этом
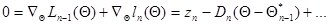 (7.5.21)
(7.5.21)
где
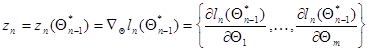 (7.5.22)
(7.5.22)
- вектор градиента функции 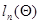 в точке
в точке 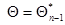 ; слагаемое
; слагаемое 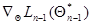 обращается в нуль благодаря тому, что
обращается в нуль благодаря тому, что 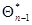 , является решением уравнения правдоподобия для предыдущего (п - 1)-го шага:
, является решением уравнения правдоподобия для предыдущего (п - 1)-го шага:
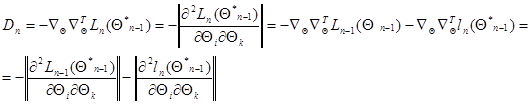 (7.5.23)
(7.5.23)
- симметричная матрица вторых производных логарифма функции правдоподобия в точке 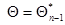 , взятая с обратным знаком, аненаписанные члены разложения имеют квадратичный и более высокий порядок малости относительно разности
, взятая с обратным знаком, аненаписанные члены разложения имеют квадратичный и более высокий порядок малости относительно разности 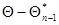 . Пренебрегая этими последними, получаем следующее приближенное решение уравнения максимального правдоподобия:
. Пренебрегая этими последними, получаем следующее приближенное решение уравнения максимального правдоподобия:
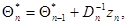 (7.5.24)
(7.5.24)
где 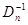 - матрица, обратная
- матрица, обратная 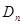 .
.
Это решение представлено в форме рекуррентного соотношения, определяющего очередное значение оценки 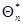 через оценку
через оценку 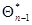 на предыдущем шаге и поправку
на предыдущем шаге и поправку 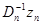 , зависящую от имеющихся данных наблюдения непосредственно и через предыдущую оценку. Поправка формируется как произведение градиента логарифма условной плотности вероятности
, зависящую от имеющихся данных наблюдения непосредственно и через предыдущую оценку. Поправка формируется как произведение градиента логарифма условной плотности вероятности 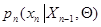 вновь полученного значения хn в точке
вновь полученного значения хn в точке 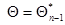 , равной предыдущей оценке, на весовую матрицу
, равной предыдущей оценке, на весовую матрицу 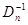 . Последняя определяется выражением (7.5.23) и также зависит от оценки
. Последняя определяется выражением (7.5.23) и также зависит от оценки 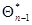 на предыдущем шаге, а ее зависимость от новых данных наблюдения целиком определяется видом логарифма условной плотности вероятности
на предыдущем шаге, а ее зависимость от новых данных наблюдения целиком определяется видом логарифма условной плотности вероятности 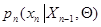 .
.
По форме соотношение (7.5.24) очень похоже на (7.5.8), реализующее итеративный способ вычисления оценки максимального правдоподобия по методу Ньютона. Однако на самом деле они существенно отличаются друг от друга. В (7.5.8) поправка к предыдущему значению оценки определяется величиной градиента логарифма всей функции правдоподобия, который всегда зависит от всех имеющихся данных наблюдения 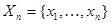 , что требует запоминания всей этой совокупности. В соответствии с (7.5.24) поправка к
, что требует запоминания всей этой совокупности. В соответствии с (7.5.24) поправка к 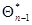 определяется величиной градиента
определяется величиной градиента 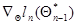 , который благодаря свойствам условной плотности вероятности
, который благодаря свойствам условной плотности вероятности 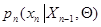 фактически зависит только от тех значений
фактически зависит только от тех значений 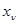 (
( 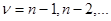 ), которые находятся в сильной статистической связи с хn. Это различие является следствием специального выбора предыдущего приближения
), которые находятся в сильной статистической связи с хn. Это различие является следствием специального выбора предыдущего приближения 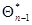 как оценки максимального правдоподобия, найденной по уменьшенной на одно значение совокупности данных наблюдения
как оценки максимального правдоподобия, найденной по уменьшенной на одно значение совокупности данных наблюдения 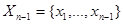 , и особенно ярко проявляется при независимых значениях
, и особенно ярко проявляется при независимых значениях 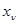 (
( 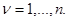 ). В этом последнем случае
). В этом последнем случае
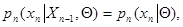
благодаря чему 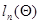 зависит только от
зависит только от 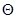 и хn, а градиент
и хn, а градиент 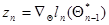 - только от предыдущего значения оценки
- только от предыдущего значения оценки 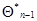 и вновь полученных на п-мшаге данных наблюдения
и вновь полученных на п-мшаге данных наблюдения 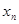 . Поэтому при независимых значениях
. Поэтому при независимых значениях 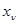 для формирования вектора
для формирования вектора 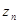 не требуется запоминать с предыдущего шага никакой иной информации, кроме значения оценки
не требуется запоминать с предыдущего шага никакой иной информации, кроме значения оценки 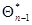 .
.
Аналогично, в случае марковской последовательности данных наблюдения, то есть при
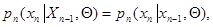
вектор 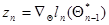 зависит только от
зависит только от 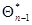 , текущего
, текущего 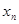 и одного предыдущего значения
и одного предыдущего значения 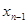 .В этом случае для вычисления
.В этом случае для вычисления 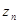 требуется запомнить с предыдущего шага, помимо значения
требуется запомнить с предыдущего шага, помимо значения 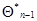 , еще только значение
, еще только значение 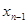 , но не всю совокупность данных наблюдения, как в итеративной процедуре. В общем случае для вычисления
, но не всю совокупность данных наблюдения, как в итеративной процедуре. В общем случае для вычисления 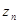 может потребоваться запоминание большего числа предыдущих значений
может потребоваться запоминание большего числа предыдущих значений 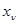 (
( 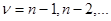 ), однако из-за необходимости учета только тех значений
), однако из-за необходимости учета только тех значений 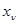 , которые статистически зависимы с
, которые статистически зависимы с 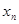 , это число практически всегда меньше полного объема совокупности данных наблюдения
, это число практически всегда меньше полного объема совокупности данных наблюдения 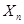 . Так, если вектор
. Так, если вектор 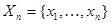 описывает временную последовательность, то количество подлежащих запоминанию членов этой последовательности определяется временем ее корреляции, а относительная их доля убывает обратно пропорционально n, как и в случае независимых значений
описывает временную последовательность, то количество подлежащих запоминанию членов этой последовательности определяется временем ее корреляции, а относительная их доля убывает обратно пропорционально n, как и в случае независимых значений 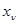 .
.
Рассмотрим теперь структуру весовой матрицы 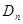 , входящей в рекуррентное соотношение (7.5.24). Согласно определению (7.5.23), из-за наличия слагаемого
, входящей в рекуррентное соотношение (7.5.24). Согласно определению (7.5.23), из-за наличия слагаемого 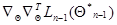 она, вообще говоря, зависит от всех значений
она, вообще говоря, зависит от всех значений 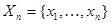 даже при независимых значениях
даже при независимых значениях 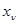 , что лишает рекуррентное соотношение (7.5.24) преимуществ, связанных с возможным сокращением количества запоминаемых с предыдущего шага данных. Существует несколько способов приближенного вычисления матрицы
, что лишает рекуррентное соотношение (7.5.24) преимуществ, связанных с возможным сокращением количества запоминаемых с предыдущего шага данных. Существует несколько способов приближенного вычисления матрицы 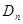 ,которые устраняют этот недостаток.
,которые устраняют этот недостаток.
Первый из них основан на более последовательном использовании основного предположения о малом различии двух очередных значений оценки 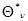 и
и 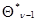 , которое является основой для получения рекуррентного соотношения (7.5.24). Это позволяет получить аналогичное рекуррентное соотношение для весовой матрицы
, которое является основой для получения рекуррентного соотношения (7.5.24). Это позволяет получить аналогичное рекуррентное соотношение для весовой матрицы 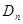 .Действительно, используя малость
.Действительно, используя малость 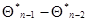 из (7.5.23), имеем
из (7.5.23), имеем
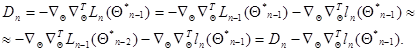 (7.5.25)
(7.5.25)
Введя обозначение
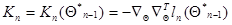 , (7.5.26)
, (7.5.26)
из (7.5.24) и (7.5.25) получим систему рекуррентных соотношений для вектора 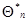 и весовой матрицы
и весовой матрицы 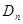
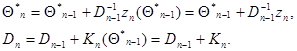 (7.5.27)
(7.5.27)
Эта система совместно с начальными значениями 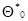 и
и 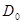 полностью определяет значение оценки
полностью определяет значение оценки 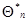 на любом шаге, требуя на каждом из них вычисления только градиента
на любом шаге, требуя на каждом из них вычисления только градиента 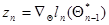 и матрицы вторых производных
и матрицы вторых производных 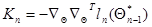 от логарифма условной плотности вероятности для текущего наблюдаемого значения
от логарифма условной плотности вероятности для текущего наблюдаемого значения 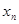 . Начальные значения выбираются с учетом имеющихся априорных данных о возможных значениях и диапазоне изменения параметров
. Начальные значения выбираются с учетом имеющихся априорных данных о возможных значениях и диапазоне изменения параметров 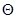 , а при полном отсутствии этих данных принимаются нулевыми (
, а при полном отсутствии этих данных принимаются нулевыми ( 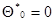 ,
, 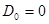 ).
).
При независимых значениях 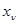 система рекуррентных соотношений (7.5.27), очевидно, описывает многомерный (размерности
система рекуррентных соотношений (7.5.27), очевидно, описывает многомерный (размерности 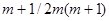 ) марковский случайный процесс, компонента которого
) марковский случайный процесс, компонента которого 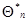 сходится к истинному значению параметра
сходится к истинному значению параметра 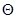 , а компонента
, а компонента 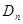 сходится к информационной матрице Фишера
сходится к информационной матрице Фишера 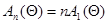 (7.3.8), где
(7.3.8), где 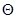 - истинное значение оцениваемого параметра, и неограниченно увеличивается с ростом п. Аналогичные свойства сходимости система (7.5.27) имеет и при более общихусловиях, если последовательность
- истинное значение оцениваемого параметра, и неограниченно увеличивается с ростом п. Аналогичные свойства сходимости система (7.5.27) имеет и при более общихусловиях, если последовательность 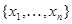 является эргодической.
является эргодической.
Второй из упомянутых способов основан на замене матрицы вторых производных от логарифма функции правдоподобия 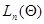 ее математическим ожиданием - информационной матрицей Фишера, которая с учетом (7.5.16) может быть записана в виде:
ее математическим ожиданием - информационной матрицей Фишера, которая с учетом (7.5.16) может быть записана в виде:
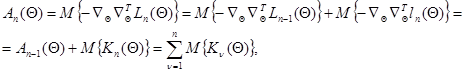 (7.5.28)
(7.5.28)
где аналогично (7.5.26)
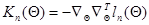 . (7.5.29)
. (7.5.29)
Заменяя в (7.5.24) матрицу 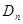 матрицей
матрицей 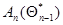 , получаем рекуррентное соотношение
, получаем рекуррентное соотношение
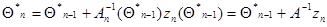 (7.5.30)
(7.5.30)
для приближенного вычисления оценок максимального правдоподобия, предложенное Сакрисоном (в оригинале для независимых одинаково распределенных 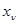 , когда
, когда 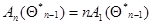 и
и 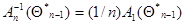 . Это рекуррентное соотношение проще системы (7.5.27), поскольку оптимальная весовая матрица
. Это рекуррентное соотношение проще системы (7.5.27), поскольку оптимальная весовая матрица 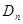 заменена ее математическим ожиданием, и для ее нахождения не требуются имеющиеся данные наблюдения, кроме тех, которые сконцентрированы в значении оценки
заменена ее математическим ожиданием, и для ее нахождения не требуются имеющиеся данные наблюдения, кроме тех, которые сконцентрированы в значении оценки 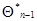 . В то же время очевидно, что подобная замена означает необходимость выполнения дополнительного по сравнению с (7.5.27) требования близости матрицы вторых производных к своему математическому ожиданию.
. В то же время очевидно, что подобная замена означает необходимость выполнения дополнительного по сравнению с (7.5.27) требования близости матрицы вторых производных к своему математическому ожиданию.
Если плотность распределения вероятности 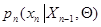 и матрица
и матрица 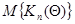 меняются от шага к шагу, прямое нахождение
меняются от шага к шагу, прямое нахождение 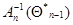 на каждом шаге может потребовать слишком большого числа вычислений. При этом за счет дополнительного уменьшения точности результатов, определяемого неравенством нулю малых разностей
на каждом шаге может потребовать слишком большого числа вычислений. При этом за счет дополнительного уменьшения точности результатов, определяемого неравенством нулю малых разностей 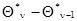 , можно перейти к рекуррентному вычислению приближенного значения матрицы
, можно перейти к рекуррентному вычислению приближенного значения матрицы 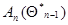 . Возвращаясь к прежнему обозначению
. Возвращаясь к прежнему обозначению 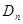 для этого приближенного значения, получаем еще одну систему рекуррентных соотношений
для этого приближенного значения, получаем еще одну систему рекуррентных соотношений
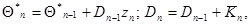 (7.5.31)
(7.5.31)
где
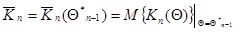 (7.5.32)
(7.5.32)
- математическое ожидание матрицы 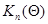 (информационная матрица Фишера для одного наблюдения
(информационная матрица Фишера для одного наблюдения 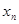 ), взятое в точке
), взятое в точке 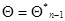 . Эта система отличается от (7.5.27) тем, что во втором из рекуррентных соотношений (7.5.31) не участвуют непосредственно данные наблюдения
. Эта система отличается от (7.5.27) тем, что во втором из рекуррентных соотношений (7.5.31) не участвуют непосредственно данные наблюдения 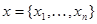 .
.
Любая из рассмотренных выше систем рекуррентных соотношений является совершенно точной, если функция 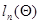 квадратично зависит от
квадратично зависит от 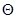 , и дополнительно матрица вторых производных
, и дополнительно матрица вторых производных 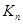 не зависит от
не зависит от 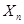 . Фактически это соответствует случаю независимых нормально распределенных (не обязательно одинаково) значений
. Фактически это соответствует случаю независимых нормально распределенных (не обязательно одинаково) значений 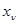 с неизвестным математическим ожиданием
с неизвестным математическим ожиданием 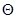 , которое и представляет собой оцениваемый параметр.
, которое и представляет собой оцениваемый параметр.
Система рекуррентных соотношений (7.5.24) дает точное решение уравнения максимального правдоподобия в гораздо более широких условиях при единственном требовании, чтобы функция 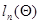 квадратично зависела от
квадратично зависела от 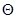 . При этом зависимость
. При этом зависимость 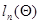 от
от 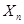 произвольна, что соответствует широкому классу распределений вероятности совокупности
произвольна, что соответствует широкому классу распределений вероятности совокупности 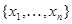 как с независимыми, так и с зависимыми значениями.
как с независимыми, так и с зависимыми значениями.
Наряду с рассмотренными общими способами существует еще ряд методов выбора матрицы весовых коэффициентов 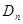 в рекуррентном соотношении (7.5.24), приспособленных к тем или иным конкретным ограничениям. Простейшим из них является выбор
в рекуррентном соотношении (7.5.24), приспособленных к тем или иным конкретным ограничениям. Простейшим из них является выбор 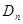 в виде диагональной матрицы, так что
в виде диагональной матрицы, так что 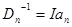 , (I - единичная матрица), где
, (I - единичная матрица), где 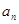 - убывающая последовательность числовых коэффициентов, выбираемая независимо от свойств функции правдоподобия так же, как в процедуре стохастической аппроксимации Робинса - Монро, которая будет рассмотрена в следующих главах.
- убывающая последовательность числовых коэффициентов, выбираемая независимо от свойств функции правдоподобия так же, как в процедуре стохастической аппроксимации Робинса - Монро, которая будет рассмотрена в следующих главах.
Стоит отметить, что любые итерационные или рекуррентные процедуры нахождения оценок максимального правдоподобия в общем случае являются приближенными. Поэтому, вообще говоря, для оценок, получающихся в результате применения этих процедур, состоятельность, асимптотическую эффективность и асимптотическую нормальность нужно доказывать заново. Для итеративных процедур необходимые свойства оценок гарантируются тем, что в принципе такие процедуры при соответствующем числе итераций дают решение уравнения правдоподобия с любой наперед заданной точностью. Для рекуррентных процедур типа (7.5.27), (7.5.30), (7.5.31) и других имеются специальные доказательства. При этом, помимо требования регулярности, предъявляются некоторые дополнительные требования:
- на поведение функции 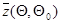 (7.2.2) при различных значениях |
(7.2.2) при различных значениях | 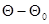 |, для достижения с помощью рекуррентной процедуры глобального максимума этой функции в точке
|, для достижения с помощью рекуррентной процедуры глобального максимума этой функции в точке 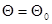 , соответствующей истинному значению параметра;
, соответствующей истинному значению параметра;
- на порядок роста вторых моментов производных логарифма функции правдоподобия при больших по модулю значениях 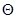 . Эти требования являются следствием более общих условий сходимости в точку всех или части компонент марковского случайного процесса, к которому приводит та или иная рекуррентная процедура.
. Эти требования являются следствием более общих условий сходимости в точку всех или части компонент марковского случайного процесса, к которому приводит та или иная рекуррентная процедура.
В заключение отметим также, что в том случае, когда существует точное решение уравнения максимального правдоподобия, оно практически всегда может быть представлено в рекуррентном виде. Приведем два простых разнородных примера. Так, элементарная оценка неизвестного математического ожидания 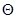 нормальной случайной величины по совокупности n ее выборочных значений
нормальной случайной величины по совокупности n ее выборочных значений 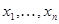 в виде арифметического среднего
в виде арифметического среднего
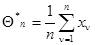 (7.5.33)
(7.5.33)
является оценкой максимального правдоподобия и может быть представлена в рекуррентном виде:
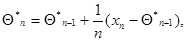 (7.5.34)
(7.5.34)
что является самым простым частным случаем (7.5.30) при
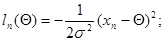
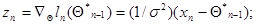 (7.5.35)
(7.5.35)
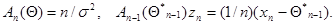
Другой пример - это нерегулярная оценка максимального правдоподобия для параметра 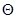 - ширины прямоугольного распределения – из (7.4.2), которая также может быть определена рекуррентным соотношением
- ширины прямоугольного распределения – из (7.4.2), которая также может быть определена рекуррентным соотношением
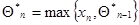 (7.5.36)
(7.5.36)
с начальным условием 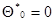 . Это рекуррентное соотношение уже другого типа: его правую часть нельзя представить в виде суммы предыдущей оценки и малой поправки, что является следствием нерегулярности этого примера; однако оно обладает всеми преимуществами рекуррентного подхода: требует запоминания с предыдущего шага всего одного числа - оценки
. Это рекуррентное соотношение уже другого типа: его правую часть нельзя представить в виде суммы предыдущей оценки и малой поправки, что является следствием нерегулярности этого примера; однако оно обладает всеми преимуществами рекуррентного подхода: требует запоминания с предыдущего шага всего одного числа - оценки 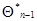 - и резко сокращает перебор до одного сравнения
- и резко сокращает перебор до одного сравнения 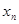 с
с 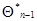 вместо сравнения всех значений
вместо сравнения всех значений 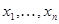 .
.
Приведенные примеры иллюстрируют преимущества рекуррентных методов даже в том случае, когда уравнение максимального правдоподобия допускает точное решение, ибо простота аналитического представления результата не тождественна вычислительной простоте его получения.
7.5.3. Переход к непрерывному времени. Дифференциальные уравнения для оценок максимального правдоподобия
Рассмотрим теперь специальный случай, когда имеющиеся данные наблюдения х описываются не совокупностью выборочных точек 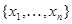 , а представляют собой отрезок реализации некоторого процесса
, а представляют собой отрезок реализации некоторого процесса 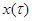 , зависящего от параметров
, зависящего от параметров 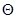 , заданный на интервале
, заданный на интервале 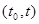 , причем длина этого интервала может увеличиваться при наблюдении (момент времени t является переменным).
, причем длина этого интервала может увеличиваться при наблюдении (момент времени t является переменным).
Для статистического описания данных наблюдения в этом случае вводится функционал отношения правдоподобия, представляющий собой предел при 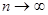 , max
, max 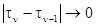 отношения плотности распределения вероятности совокупности значений
отношения плотности распределения вероятности совокупности значений 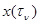
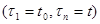 при произвольно заданном значении
при произвольно заданном значении 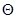 к аналогичной плотности вероятности при некотором фиксированном значении
к аналогичной плотности вероятности при некотором фиксированном значении 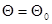 , а в некоторых случаях, когда
, а в некоторых случаях, когда 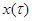 допускает представление
допускает представление 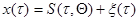 , где
, где 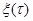 - случайный процесс, не зависящий от
- случайный процесс, не зависящий от 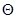 , к плотности вероятности совокупности значений
, к плотности вероятности совокупности значений 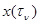 при условии, что
при условии, что 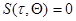 . Использование функционала отношения правдоподобия позволяет исключить формальные трудности определения плотности вероятности, возникающие при переходе к непрерывному времени.
. Использование функционала отношения правдоподобия позволяет исключить формальные трудности определения плотности вероятности, возникающие при переходе к непрерывному времени.
Логарифм функционала отношения правдоподобия может быть представлен в виде
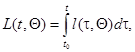 (7.5.37)
(7.5.37)
где 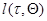 - некоторый функционал процесса
- некоторый функционал процесса 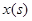 на интервале
на интервале 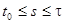 . В некоторых случаях функционал
. В некоторых случаях функционал 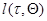 вырождается в функцию, зависящую только от значения
вырождается в функцию, зависящую только от значения 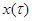 . Так, если
. Так, если
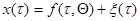 . (7.5.38)
. (7.5.38)
где 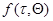 - известная функция времени
- известная функция времени 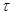 и параметров
и параметров 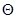 , а
, а 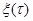 - дельта-коррелированный случайный процесс («белый» шум) со спектральной плотностью No,то, выбирая в качестве знаменателя отношения правдоподобия распределения вероятности х при
- дельта-коррелированный случайный процесс («белый» шум) со спектральной плотностью No,то, выбирая в качестве знаменателя отношения правдоподобия распределения вероятности х при 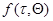 , будем иметь
, будем иметь
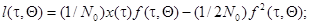 (7.5.39)
(7.5.39)
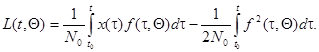 . (7.5.40)
. (7.5.40)
Пусть 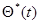 - оценка максимального правдоподобия параметра
- оценка максимального правдоподобия параметра 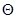 , построенная по реализации процесса
, построенная по реализации процесса 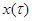 на интервале
на интервале 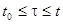 ,то есть решение уравнения максимального правдоподобия
,то есть решение уравнения максимального правдоподобия
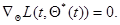 (7.5.41)
(7.5.41)
Дифференцируя левую часть этого уравнения по времени, получаем
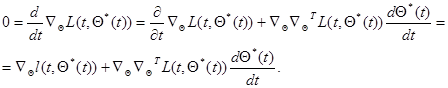 (7.5.42)
(7.5.42)
Вводя обозначения
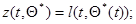 (7.5.43)
(7.5.43)
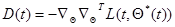 (7.5.44)
(7.5.44)
и решая уравнение (7.5.42) относительно 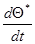 , получаем дифференциальное уравнение для оценки максимального правдоподобия
, получаем дифференциальное уравнение для оценки максимального правдоподобия
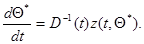 (7.5.45)
(7.5.45)
Матрица 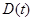 , в свою очередь, согласно (7.5.37) определяется дифференциальным уравнением
, в свою очередь, согласно (7.5.37) определяется дифференциальным уравнением
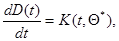 (7.5.46)
(7.5.46)
где
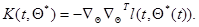 (7.5.47)
(7.5.47)
Так же, как в дискретном случае, матрица 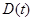 в (7.5.45), (7.5.47) может быть заменена своим математическим ожиданием — информационной матрицей Фишера
в (7.5.45), (7.5.47) может быть заменена своим математическим ожиданием — информационной матрицей Фишера 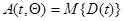 при значении
при значении 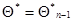 , а дифференциальное уравнение (7.5.46) для весовой матрицы
, а дифференциальное уравнение (7.5.46) для весовой матрицы 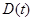 - уравнением
- уравнением
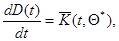 (7.5.48)
(7.5.48)
где аналогично дискретному случаю
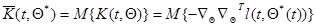 (7.5.49)
(7.5.49)
- математическое ожидание матрицы вторых производных 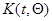 .
.
Совокупность дифференциальных уравнений (7.5.45), (7.5.46) или (7.5.45), (7.5.48) совместно с начальными условиями, относительно выбора которых остается в силе все сказанное для дискретного случая, полностью определяет оценку максимального правдоподобия 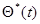 для любого момента времени. Эта совокупность может быть смоделирована с помощью соответствующих, вообще говоря, нелинейных аналоговых устройств или при подходящей дискретизации по времени решена с помощью ЭВМ. Отметим в заключение одну из модификаций этих уравнений, позволяющую избежать необходимости обращения матрицы
для любого момента времени. Эта совокупность может быть смоделирована с помощью соответствующих, вообще говоря, нелинейных аналоговых устройств или при подходящей дискретизации по времени решена с помощью ЭВМ. Отметим в заключение одну из модификаций этих уравнений, позволяющую избежать необходимости обращения матрицы 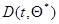 .
.
Вводя обозначение
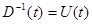 (7.5.50)
(7.5.50)
и дифференцируя по времени соотношение 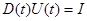 , где I - единичная матрица, получаем с помощью (7.5.46) дифференциальное уравнение, определяющее непосредственно матрицу
, где I - единичная матрица, получаем с помощью (7.5.46) дифференциальное уравнение, определяющее непосредственно матрицу 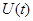 :
:
и дифференцируя по времени соотношение 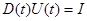 , где I - единичная матрица, получаем с помощью (7.5.46) дифференциальное уравнение, определяющее непосредственно матрицу
, где I - единичная матрица, получаем с помощью (7.5.46) дифференциальное уравнение, определяющее непосредственно матрицу 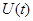 :
:
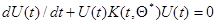 (7.5.51)
(7.5.51)
(и аналогично при замене 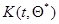 на
на 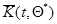 ), которое совместно с уравнением (7.5.45)
), которое совместно с уравнением (7.5.45)
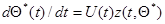
определяет оценку 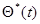 , не требуя обращения матриц. При этом имеет место переход от простейшего линейного дифференциального уравнения (7.5.46) к нелинейному относительно
, не требуя обращения матриц. При этом имеет место переход от простейшего линейного дифференциального уравнения (7.5.46) к нелинейному относительно 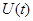 дифференциальному уравнению (7.5.51) типа Риккати.
дифференциальному уравнению (7.5.51) типа Риккати.
Дата добавления: 2020-10-14; просмотров: 492;











