Ланцюг з активним опором і індуктивністю

Ланцюг перемінного струму з елементами активного опору r та індуктивності L, з'єднаними послідовно, зображена на мал. 5.1, а. Сила струму I у такому ланцюзі залежить від прикладеної напруги u,ЕРС самоіндукції e_L, що виникає у ланцюзі, й активного опору. Тому рівняння, написане за другим законом Кірхгофа, має вид:

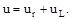
(5.1)

Якщо по ланцюгу протікає синусоїдальний струм i=I_m sin ωt, то, як установлено вище, напруга и_т на опорі r збігається за фазою зі струмом, а напруга и_L на індуктивності L випереджає струм на л/2. Отже, напруга на затисках усього ланцюга буде дорівнювати:

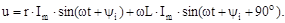
Геометричне підсумовування векторів показано на векторнійдіаграмі (рис. 5.1, в). Приймаючи вектор сили струму І за вихідний, відкладаємо вектор 1·R=u_R по напрямку вектора струму,а вектор и_L=1·X_L під кутом π/2 убік випередження вектора струму. Геометрична сума цих векторів дорівнює векторові прикладеної напруги u. Таку діаграму називають трикутником напруг, з якого одержуємо розв'язання рівняння щодо сили струму I. Вирази (5.2 та 5.3) подають закон Ома для діючих значень струму та напруги:

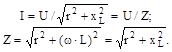
(5.2) (5.3)

Z – називається повним опором нерозгалуженого ланцюга з активним опором та індуктивністю.

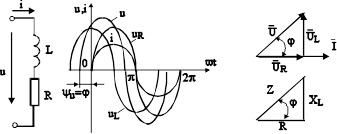
а) б) в)

Рис. 5.1. Нерозгалужений ланцюг з елементами R і L

та його діаграми

Якщо всі сторони трикутника напруг зменшити в I раз, то одержимо трикутник опорів (рис. 5.1, г). Кутзрушення між струмом і напругою можна знайти з трикутників напруг або опорів за формулою:

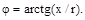
(5.4)

Зрушення за фазою між напругою й струмом, обумовлено індуктивністю, завжди позитивне.

5.2. Ланцюг із ємністю.

Ланцюг перемінного струму з ємністю С показано на рис. 5.2, а.

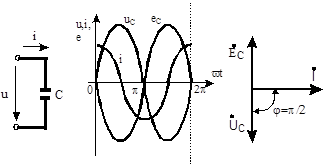
а) б) в)

Рис. 5.2. Ланцюг з елементом С і його діаграми

Якщо на затиски такого ланцюга подати синусоїдальну напругу u=U_m sin ωt, то при її збільшенні елемент ємності (конденсатор) буде заряджатися, а при зменшенні – розряджатися. У результаті на обкладках конденсатора буде відбуватися зміна заряду зі швидкістю:

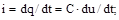
(5.5)

де Uс — напруга на затисках конденсатора, що має назву ємнісна напруга.

Оскільки напруга на затисках конденсатора змінюється за синусоїдальним законом u= U_m sin(ωt + ψ_u) то сила струму у ланцюзі, що містить ємність, буде:

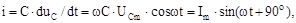
(5.6)

де I_m = ω·C·U_cm—амплітуда сили струму.

Величина х_с=1/(ωС) = 1/(2πfС), що має розмірність опору, називається ємнісним опором, а величина, зворотна їй b_С = 1/X_C , називається ємнісною провідністю.

Ємнісний опір є розрахунковою величиною, за допомогою якої враховується вплив зміни електричного поля конденсатора на струм ланцюга. Зіставлення рівнянь для струму й напруги показує, що в ланцюзі з ємністю напруга відстає від струму на чверть періоду. Це наочно показують часова (рис. 5.1, б) і векторна (рис. 5.2, в)діаграми.

5.3. Ланцюг з активним опором і ємністю.

Ланцюг перемінного струму з елементами активного опору r і ємності С, з'єднаними послідовно, зображений на рис. 5.3, а. Сила струму I у такому ланцюзі залежить від докладеної напруги u, напруги u_С = (1/C) ∫ idt, створюваної на ємності С, і опору r. Тому рівняння електричної рівноваги ланцюга відповідно до другого закону Кірхгофа має вид:

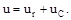
(5.7)

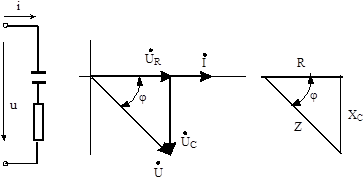
а) б) в)

Рис. 5.3. Нерозгалужений ланцюг з елементами R і С та його діаграми

Якщо по ланцюгу проходить синусоїдальний струм, то напруга и_R на опорі r збігається за фазою зі струмом, а напруга u_C на ємності C відстає від струму на чверть періоду, то рівняння приймає вид:

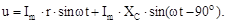
Склавши ординати миттєвих значень напруг (мал. 4.9,6), знаходимо:

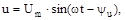
(5.8)

тому що початкова фаза ψ_i = 0 і, отже, ψ_u = φ.

Таким чином, спадання напруги на ділянках ланцюга й напруга на затисках усього ланцюга змінюються за синусоїдальним законом. Рівняння електричної рівноваги для векторів діючих значень напруг має вигляд:

.

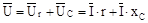(5.9)

Геометричне підсумовування векторів показане на діаграмі напруг (мал. 5.3, в).Розв’язання рівняння щодо сили струму в ланцюзі виражає закон Ома для ланцюга з активним опором і ємністю:

,

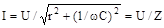(5.10)

де

.

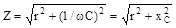(5.11)

Z – зветься повним опором нерозгалуженого ланцюга з активним опором і ємністю.

Зменшивши всі сторони трикутника напруг у I раз, одержимо трикутник опорів (рис. 5.3,г), з якого знаходиться кут зрушення між напругою і струмом.

Зрушення за фазою, між напругою й струмом, обумовлене ємністю, завжди негативне.

5.4. Ланцюг з активним опором, індуктивністю і ємністю.

Ланцюг перемінного струму з елементами активного опору r, індуктивності L і ємності З, з'єднаними послідовно, зображена на рис. 5.4, а. Рівняння електричної рівноваги діючих значень напруги на затисках ланцюга у відповідності з другим законом Кірхгофа визначається геометричною сумою векторів:

На рис. 5.4. б зображені векторні діаграми при U_L>U_C і U_L<U_C відповідно. При U_L= U_C вектори напруги й струму збігаються за фазою:

.

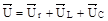
Діюча реактивна напруга U_р визначиться алгебраїчною сумою векторів U_L і U_C.

Опір х = (ωL – 1/ωC) називається реактивним опором; Х>0 при Х_L>X_C; X<0 при X_L<Хс; Хх=0 при Х_L =X_C.

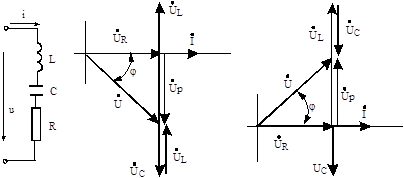
а) б) в)

Рис. 5.4. Нерозгалужений ланцюг з елементами r, I і С та його векторна діаграма

З векторних діаграм напруг (див. рис. 5.4 б, в) знаходимо силу струму у ланцюзі:

,

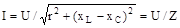(5.12)

яка являє собою закон Ома, а величина:

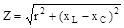
(5.13)

є повним опором ланцюга.

Зрушення по фазі між струмом і напругою визначиться (див. рис. 4.10 6, в) виразом:

.

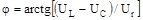(5.14)

У залежності від співвідношення індуктивного і ємнісного опорів різниця фаз напруги й струму може бути позитивною, негативною або рівною нулеві.