ОСНОВНЫЕ СВОЙСТВА И ХАРАКТЕРИСТИКИ ПОЛУПРОВОДНИКОВ

Параметры полупроводниковых приборов зависят от электропроводности материалов и, следовательно, от закономерностей протекания токов в отдельных частях приборов.

Уровень Ферми, температурный потенциал. При рассмотрении принципа работы различных полупроводниковых приборов важную роль играет понятие электрохимического потенциала, или уровня Ферми. Уровень Ферми для полупроводника - это энергия, которая является функцией концентрации носителей заряда. Зная уровень Ферми, можно вычислить концентрации носителей заряда и наоборот.

Так, концентрация электронов в зоне проводимости

(1.4)

где F - энергия уровня Ферми; 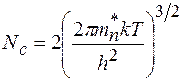- эффективная плотность состояний в зоне проводимости; 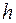- постоянная Планка; 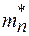- эффективная масса электрона; - энергия нижней границы зоны проводимости; k – постоянная Больцмана; T – абсолютная температура.

Аналогично (1.4) концентрация дырок

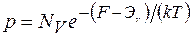, (1.5)

где 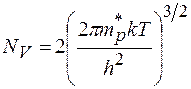- эффективная плотность состояний в валентной зоне; - энергия верхней границы валентной зоны; - эффективная масса дырки.

Из этих выражений следует, что

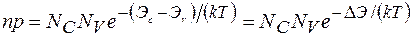(1.6)

где 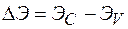- ширина запрещенной зоны.

Так как при определенной температуре все члены, входящие в последнее уравнение, постоянны (при T=const, N_C=const, ΔЭ=const) то

.

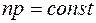Таким образом, следует важный вывод.

В равновесном состоянии произведение концентраций носителей зарядов для данного полупроводника при определенной температуре есть величина постоянная, не зависящая от концентрации и распределения примесей.

Понятие эффективной массы дырки, введенное в связи с тем, что характеры движения электронов и дырок отличаются в результате различного воздействия на них электрических полей, позволяет рассматривать поведение дырки, движущейся в валентной зоне, так же, как поведение электрона в зоне проводимости. Разница состоит только в различии эффективных масс обоих типов носителей. Следует отметить, что масса электрона в кристалле в общем случае не совпадает с его массой в вакууме. Поэтому понятие эффективной массы введено и для электрона.

Если полупроводник имеет собственную электропроводность теплового происхождения, когда дырки с концентрацией и электроны с концентрацией образуются парами и , то уровень Ферми при условии 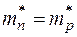лежит почти в середине запрещенной зоны.

Решив уравнения (1.4) и (1.5) для концентраций носителей зарядов в равновесном полупроводнике с примесной электропроводностью получим следующие выражения для энергий уровня Ферми:

,

,

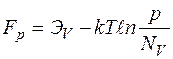где 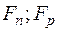- уровни Ферми в полупроводниках n- и р-типа; - концентрации электронов и дырок.

Если значения энергий уровня Ферми разделить на заряд электрона q, все приведенные выражения останутся справедливыми, только в них вместо энергий будут стоять значения соответствующих потенциалов Ферми:

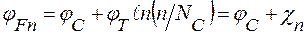; (1.7,а)

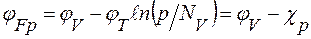, (1.7,б)

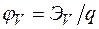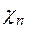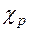где - температурный потенциал; - потенциал нижней границы зоны проводимости; - потенциал верхней границы валентной зоны; и - химические потенциалы;

; .

Название «температурный потенциал» для величины 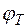вполне оправдано, поскольку она имеет размерность напряжения и пропорциональна температуре. С физической точки зрения температурный потенциал есть выраженная в электрических единицах статистическая температура или близкая к ней средняя кинетическая энергия свободного электрона в электрическом газе. Полезно запомнить, что при температуре 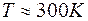(которую мы условно будем называть «комнатной» температурой 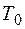) температурный потенциал равен .

Физический смысл химического потенциала состоит в следующем. Химический потенциал является однозначной функцией концентрации соответствующих частиц. Поэтому наличие разности химических потенциалов означает наличие разности концентраций, а разность концентрации, естественно, вызывает перемещение – диффузию частиц в направлении от большей концентрации к меньшей. Таким образом, химический потенциал характеризует возможность диффузии свободных частиц (заряженных или не заряженных), подобно тому, как электрический потенциал характеризует возможность дрейфа свободных частиц (если они являются носителями заряда). Учитывая приведенные выражения для 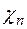и 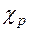, приходим к выводу, что потенциал Ферми, отсчитанный от границы той или иной зоны (т. е. без учета потенциальной энергии), есть химический потенциал соответствующих носителей. В общем же виде потенциал Ферми есть сумма электрического и химического потенциалов.

Отсюда следует еще одно название потенциала Ферми - электрохимический потенциал. Градиент потенциала Ферми, будучи суммой градиентов электрического и химического потенциалов, позволяет одновременно характеризовать оба типа движения носителей – диффузию и дрейф.

Как следствие в условиях равновесия, когда направленного движения носителей нет, должно выполняться условие т. е.

.

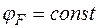Постоянство («горизонтальность») уровня Ферми в равновесной системе является одним из фундаментальных соотношений теории твердого тела. Иначе говоря, в равновесной системе могут иметь место градиенты электрического и химического потенциалов и соответственно дрейфовые и диффузионные потоки носителей, но эти потоки должны взаимно уравновешиваться (больцмановское равновесие).

Концентрация носителей зарядов. В собственном полупроводнике концентрации свободных электронов и дырок одинаковы: . Тогда из формул (1.4), (1.5) и (1.6) следует, что при любой температуре уровень Ферми собственного полупроводника расположен вблизи середины запрещенной зоны, т. е. 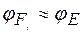. Подставляя в формулу (1.6), легко получаем концентрации свободных электронов и дырок в собственном полупроводнике:

,

где 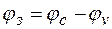- ширина запрещенной зоны.

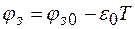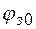Ширина запрещенной зоны – один из важнейших параметров полупроводников: он определяет энергию, необходимую для образования электронно-дырочных пар. Ширина запрещенной зоны зависит от температуры: , где - ширина запрещенной зоны при 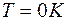; 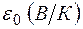- температурная чувствительность. Для кремния , , отсюда при комнатной температуре.

Зависимость собственных концентраций и 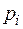от температуры очень сильна и обусловлена в основном изменением температурного потенциала в показателе экспоненты, а не степенным множителем Т³/². Столь же сильно зависит собственная концентрация от ширины запрещенной зоны при данной температуре. Так, сравнительно небольшое различие в значении 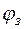у германия и кремния (0,67 и 1,11 В) приводит к различию собственных концентраций при комнатной температуре более чем на 3 порядка. Формулу (1.6) можно записать в более компактной форме:

(1.8)

которую и будем использовать в дальнейшем.

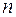Используя формулы (1.8), (1.4) и (1.5) и полагая , нетрудно выразить концентрации и 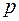через собственную концентрацию :

,

.

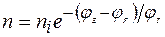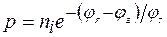Отсюда легко получить потенциал Ферми в двух формах:

;

,

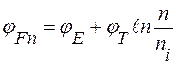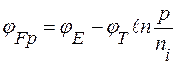где - потенциал середины запрещенной зоны, который называют также электростатическим потенциалом полупроводника.

Для того чтобы определить потенциал 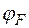, нужно знать концентрации свободных носителей.

При оценке значени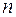й и 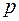используют условие нейтральности (точнее, квазинейтральности) полупроводника. Это важное условие формулируется следующим образом: в однородном полупроводнике не может быть существенных объемных некомпенсированных зарядов ни в равновесном состоянии, ни при наличии тока.

Поэтому в общем виде условие нейтральности для единичного объема записывают так:

,

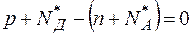где , 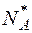— концентрации ионизированных доноров и акцепторов. Уравнение говорит о том, что концентрация частиц, несущих положительный заряд (дырки и ионизированные доноры), равна концентрации частиц, несущих отрицательный заряд (электроны и ионизированные акцепторы).

Для электронных полупроводников, не содержащих акцепторов,

.

Для дырочных полупроводников, не содержащих доноров,

.

Перейдем непосредственно к оценке концентраций свободных носителей. Рассмотрим сначала электронные полупроводники. В типичном электронном полупроводнике выполняется неравенство . Кроме того, в рабочем диапазоне температур донорные атомы практически полностью ионизированы, т. е. . Тогда получаем концентрацию свободных электронов 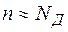, которая, как видим, определяется концентрацией примеси и, следовательно, не зависит от температуры. Поскольку 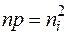, то получим концентрацию свободных дырок , которая очень сильно — экспоненциально — зависит от температуры. Наконец, находим уровень Ферми в типичном электронном полупроводнике:

.

Как видим, уровень Ферми в электронном полупроводнике лежит тем выше, чем больше концентрация доноров и чем меньше температура.

Однако следует иметь в виду, что полученные выражения действительны в ограниченном температурном диапазоне: с понижением температуры степень ионизации доноров уменьшается и принятое равенство становится менее строгим. С повышением температуры увеличивается концентрация собственных носителей и постепенно нарушается принятое неравенство (электронный полупроводник превращается в собственный).

Случай дырочного полупроводника, в котором 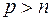, нет необходимости рассматривать столь же подробно. Если акцепторы полностью ионизированы и температура ниже критической, то получаем аналогичные соотношения, характерные для ярко выраженного дырочного полупроводника:

, ,

.

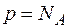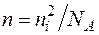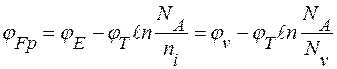Как видим, уровень Ферми в дырочном полупроводнике лежит тем ниже, чем больше концентрация акцепторов и чем меньше температура.

Из приведенных выше уравнений следует, что увеличение количества электронов при данной температуре всегда вызывает пропорциональное уменьшение количества дырок и наоборот.

Так как при данной температуре количество электронов и дырок постоянно, то рекомбинация одной пары вызовет генерацию электрона и дырки в другом месте. Рекомбинация и генерация дырок и электронов в полупроводнике происходят непрерывно.

В зависимости от характера процессов различают несколько видов рекомбинаций.

При межзонной рекомбинации электроны из зоны проводимости непосредственно переходят в валентную зону. При этом выделяется энергия, равная ширине запрещенной зоны . Эта энергия выделяется или в виде фотона (излучательная рекомбинация) или в виде фонона (безизлучательная рекомбинация). Характер излучения зависит от строения зон полупроводника. Если экстремумы зон совпадают, в реальном полупроводнике ширина запрещенной зоны меняется в зависимости от геометрической координаты и при переходе электрона значение его импульса остается постоянным, энергия 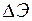выделяется в виде фотона. При несовпадении экстремумов обычно имеет место безизлучательная рекомбинация с выделением фонона.

В большинстве полупроводников, используемых в настоящее время, рекомбинация осуществляется через рекомбинационные центры, которые называют рекомбинационными ловушками или просто ловушками. Ловушки - это атомы примесей или дефекты кристаллической структуры, энергетические уровни которых находятся в запрещенной зоне, как правило, достаточно далеко как от валентной зоны, так и от зоны проводимости. Электрон из зоны проводимости может перейти на энергетический уровень ловушки (переход 1 на рис. 1.4) и затем либо вернуться назад (переход 2), либо перейти в валентную зону (переход 3). В последнем случае произойдет восстановление валентной связи. Рекомбинация носит ступенчатый своеобразный характер, и энергия 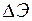выделяется двумя порциями. Аналогичным двухступенчатым путем может происходить и генерация зарядов.

Поверхностная рекомбинация обусловлена тем, что на поверхности кристалла в результате ее окисления, адсорбции атомов примесей, наличия дефектов кристаллической решетки, вызванных механической обработкой, появляются поверхностные состояния, энергетические уровни которых лежат в запрещенной зоне.

Законы движения носителей заряда в полупроводниках. В общем случае в полупроводнике имеются градиент концентрации примесей, создающих электропроводность, и градиент электрического поля. Поэтому движение носителей заряда обусловлено двумя процессами: диффузией (под влиянием градиента концентраций) и дрейфом. Плотность токов дрейфа можно оценить, воспользовавшись выражениями (1.2).

Плотности диффузионных составляющих тока пропорциональны градиентам химических потенциалов 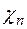и 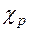, которые для невырожденных полупроводников выражаются формулами (1.7). Поэтому в одномерном случае имеем:

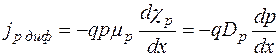; (1.9,а)

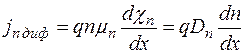. (1.9,б)

Здесь и — коэффициенты диффузии дырок и электронов, связанные с подвижностями тех же носителей формулой Эйнштейна .

Знак минус имеет следующий физический смысл: диффузия всегда происходит в направлении убывания концентрации, а поскольку дырки несут положительный заряд, ток 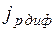должен быть положительным при .

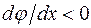Плотность суммарного диффузионного тока

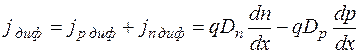(1.10)

Плотность тока, протекающего в полупроводнике, складывается из диффузионной и дрейфовой составляющих плотности тока:

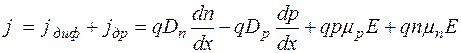(1.11)

Из уравнения (1.11) видно, что для определения плотности тока в полупроводнике необходимо знать концентрации носителей заряда и напряженность поля E.

В общем случае концентрации р и n зависят от двух переменных: координаты x и времени 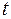. Поэтому для определения токов нужно предварительно найти функци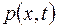и и . Эти функции являются решениями так называемых уравнений непрерывности потока, которым в любой момент времени подчиняется движение носителей.

Для дырок и электронов уравнения непрерывности записываются в следующем виде :

; (1.12,а)

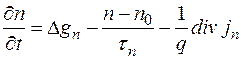, (1.12,б)

где 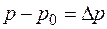и — и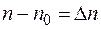збыточные концентрации; и — скорости генерации под действием внешних факторов, например света; , 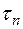- времена жизни носителей заряда.

Слагаемые в правых частях (1.12) соответствуют возможным причинам изменения концентрации носителей во времени. В частности, последние слагаемые можно рассматривать как скорости накопления или рассасывания носителей, обусловленные неравенством потоков, втекающих и вытекающих из некоторого элементарного объема. Такой небаланс потоков характеризуется дивергенцией вектора плотности потока. В нашем случае плотность потока есть 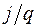. Дивергенция этого вектора в одномерном случае равна:

.

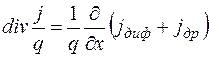Подставляя сюда соотношения (1.2) и (1.10), получаем:

;

.

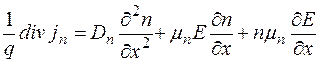С учетом этих выражений, а также при отсутствии внешних факторов (свет, радиация и т. п.) уравнения непрерывности (1.12) принимают следующую форму:

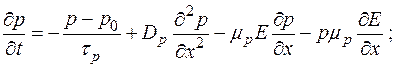(1.13,а)

(1.13,б)

Из этих уравнений следует вывод.

Изменение концентраций носителей заряда в полупроводнике с течением времени происходит из-за их рекомбинации (первые члены правых частей), перемещений вследствие диффузии (вторые члены), и дрейфа (третьи и четвертые члены).

В том случае, когда поле отсутствует или когда его влиянием заведомо можно пренебречь, полагаем Е = 0. При этом выражения (1.13) упрощаются и носят название уравнений диффузии:

.

Уравнения диффузии позволяют достаточно строго анализировать многие типы полупроводниковых приборов.

Диэлектрическая релаксация. Пусть в ограниченном объеме полупроводника удалось сосредоточить избыточные концентрации электронов и дырок, так что образовался объемный заряд с плотностью . Под действием возникшего поля заряд будет рассасываться, т. е. носители будут покидать тот начальный объем, в котором они были сосредоточены. Такое рассасывание заряда под действием собственного поля носит название диэлектрической релаксации, или релаксации Максвелла.

При анализе диэлектрической релаксации пренебрегают рекомбинацией носителей и их диффузией, чтобы выделить явление в чистом виде. Следовательно, в правых частях (1.13) можно опустить все члены, кроме последних:

.

Вычитая второе уравнение из первого, получаем уравнение релаксации:

.

Решением уравнения релаксации является экспоненциальная функция

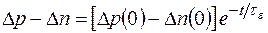, (1.14)

где — избыточная начальная концентрация и — время диэлектрической релаксации.

Величина 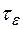характеризует время, в течение которого нарушена нейтральность полупроводника: через (3 4) 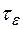объемный заряд практически рассасывается и нейтральность восстанавливается.

Время релаксации помимо диэлектрической проницаемости зависит от удельной проводимости или удельного сопротивления. Например, если 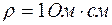, то для германия и кремния 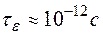. Такое крайне малое значение типично для процессов диэлектрической релаксации и является одной из основ квазинейтральности полупроводников.

Таким образом, если в полупроводник введено разное количество электронов и дырок, то разность концентраций носителей заряда противоположного знака стремится к нулю, уменьшаясь по экспоненциальному закону. Время диэлектрической релаксации не более 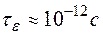. Поэтому процесс уравновешивания зарядов одного знака зарядами другого знака происходит за очень короткий промежуток времени.

Обычно различают два механизма обеспечения условия электронейтральности.

Если в полупроводник с электропроводностью определенного типа, например p, ввести некоторое количество дырок, концентрация которых равна , то они уходят из начального объема, изменяя свою концентрацию в соответствии с выражением

,

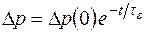Если в полупроводник n-типа ввести дополнительные дырки, концентрация которых , то электроны из объема полупроводника под действием электрического поля приходят в область объема, куда были введены дырки, компенсируя заряд последних. В итоге в этом объеме через время . окажется дополнительный заряд электронов 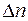, равный заряду введенных дырок :

.

Таким образом, если возмущение было вызвано основными носителями заряда, то рассасывание их произойдет за малый промежуток времени. Если возмущение вызвано не основными для данного полупроводника носителями заряда, то в течение короткого времени в полупроводнике появится дополнительный заряд основных носителей, компенсирующий заряд неосновных носителей.

Если возмущение, в результате которого появилась дополнительная концентрация носителей заряда в полупроводнике, закончилось, то эти заряды в результате рекомбинации рассасываются, причем их концентрация убывает до равновесной по экспоненциальному закону

,

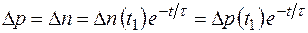где 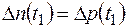- концентрации носителей заряда в момент прекращения возмущения и окончания процесса нейтрализации; - время жизни носителей заряда.

Время жизни носителей заряда , поэтому рассасывание заряда происходит значительно дольше, чем его нейтрализация.