Разрядка конденсатора на индуктивность

Рассмотрим явления в – цепи, представленной рис. , когда конденсатор, заряженный до напряжения замыкается на идеальную катушку ( .

В начальный момент времени напряжение на конденсаторе имеет наибольшее значение, и в электрическом поле конденсатора запасена энергия

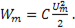(11-21)

При замыкании рубильника конденсатор начнет разряжаться, и в цепи возникает электрический ток. Вместе с током создается магнитное поле, а следовательно, и эдс самоиндукции, которая в каждый момент равна и противоположна напряжению на конденсаторе, так как для этой цепи по второму закону Кирхгофа справедливо соотношение

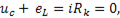
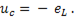(11-22)

Так как то

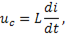
и следовательно, ток в цепи нарастает со скоростью

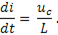
По мере того как конденсатор разряжается и падает, уменьшается и скорость нарастания тока пока, наконец, при она не упадет до нуля.

Но, с другой стороны, при равна нулю и энергия электрического поля конденсатора. Так как в рассматриваемой цепи энергия не превращается в тепло, то первоначальный запас энергии переходит в энергию магнитного поля катушки. Отсюда следует. Что при ток в цепи имеет наибольшее значение; его можно найти, приравняв первоначальный запас энергии тому значению магнитной энергии, которое имеет место при наибольшем токе:

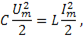
откуда

(11-23)

Величина 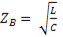имеет размерность сопротивления и называется волновым сопротивлением.

Рис.139

Разрядный ток (рис.139)

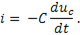
Следовательно эдс самоиндукции

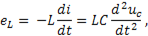
подставив это выражение в ( ), получаем дифференциальное уравнение LC- цепи

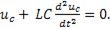(11-24)

Решением этого уравнения является выражение следующего вида:

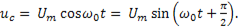(11-15)

Ток в цепи

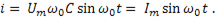(11-26)

Таким образом, в цепи протекает синусоидальный ток, и напряжение на конденсаторе изменяется периодически, хотя источник переменного тока в цепи отсутствует.

Процесс уменьшения напряжения конденсатора от первоначального значения до нуля соответствует переносу электронов с отрицательной обкладки на положительную. Разрядкой конденсатора этот процесс не заканчивается, так как ток в катушке не может меняться скачком. В цепи продолжает протекать ток прежнего направления, но уменьшающийся по величине. Наличие этого тока означает перенос электронов с электрода, бывшего ранее отрицательным, на электрод, бывший ранее положительным, благодаря чему первый начнет заряжаться положительно, а второй – отрицательно.

При отсутствии в цепи сопротивления R этот процесс будет продолжаться до тех пор, пока конденсатор не зарядится до напряжения, по величине равного начальному, но обратного по знаку. Далее конденсатор начнет разряжаться в обратном направлении, а затем снова заряжаться, и этот процесс будет продолжаться до тех пор, пока цепь не будет разомкнута.

Таким образом, в рассматриваемой цепи энергия электрического поля переходит в энергию магнитного поля, и наоборот, т.е. в цепи происходят незатухающие периодические колебания энергии.

Угловая частота этих свободных гармонических колебаний

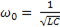(11-27)

определяется индуктивностью и емкостью рассматриваемой LC – цепи.

Разряд конденсатора на R,L – цепь. При наличии в электрической цепи активного сопротивления процесс разряда конденсатора на индуктивность будет отличаться от ранее рассмотренного только тем, что он будет сопровождаться непрерывным преобразованием электрической энергии в тепловую ( 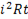). Благодаря этому амплитуды тока и напряжения с каждым полупериодом будут уменьшаться, т.е. в цепи будет происходить затухающий колебательный процесс (рис.140 а), который прекратится в тот момент, когда вся энергия будет преобразована в тепловую.

При сопротивлении разряд конденсатора будет иметь апериодический характер (рис.140 б). В этом случае напряжение на конденсаторе с начального момента разряда непрерывно уменьшается, постепенно спадая до нуля, а ток в цепи сначала увеличивается от нуля до некоторого наибольшего значения и затем непрерывно уменьшается до нуля.

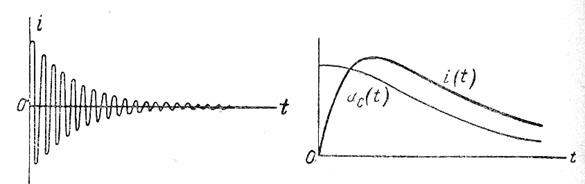
а б

Рис. 140

Контрольные вопросы

1. Какие изменения в цепи приводят к возникновению переходного процесса?

2. Как объяснить возникновение переходных процессов с энергетической точки зрения?

3. Какого типа переходные процессы могут быть?

4. Определить время, необходимое для зарядки конденсатора емкостью 40мкф через резистор сопротивлением 250 Ом.

5. Определить напряжение на конденсаторе через 20с после включения его к источнику постоянной эдс 220В. Ем кость конденсатора 40мкФ, а сопротивление цепи 250 Ом.

6. Каким образом влияют на характер кривой 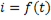при разрядке конденсатора величина его емкости и величина активного сопротивления цепи?

7. Определить время саморазрядки конденсатора со слюдяным диэлектриком, если удельное сопротивление слюды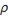

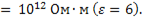
8. Определить время переходного процесса при подключении катушки к источнику постоянного напряжения, если L = 0,4Гн; R = 3Ом.

9. Что изменится в характере кривой тока (по данным задачи №8), если увеличить индуктивность катушки?

10. Какие параметры L,R –цепи влияют на образование искрового или дугового разряда при отключении катушки индуктивности?

Г л а в а 12