ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ

До сих пор все процессы в электрической цепи рассматривались как процессы неизменные во времени, т. е. процессы, при которых напряжение и токи постоянны. Эти процессы называют установившимися. Ори существуют до тех пор, пока электрическая цепь подключена к источнику питания. Всякому установившемуся процессу предшествует процесс становления или переходный процесс.

Процесс, происходящий в электрической цепи от момента подключения цепи к источнику до момента установления напряжения и тока в ней, называют переходным.

Переходный процесс может быть вызван также переходом от одного режима работы цепи к другому за счет изменения параметров цепи.

Преднамеренное или случайное изменение параметров электрической цепи называют коммутацией. Так, например, изменение сопротивления резистивного, индуктивного или емкостного элементов приводит к изменению тока в цепи.

Каждому состоянию электрической цепи соответствует определенный запас энергии электрического и магнитного полей. Если цепь содержит индуктивный или емкостной элемент, то каждому приложенному напряжению соответствует свой ток, свой магнитный поток, своя энергия электрического или магнитного поля.

При переходе цепи от одного состояния к другому энергия изменяется плавно, а не скачком.

2. Зарядка и разрядка конденсатора

Зарядка конденсатора. Если присоединить конденсатор к источнику постоянного тока (рис. 129 ), то на обкладках конденсатора, как известно, будут накапливаться электрические заряды q, т.е. будет происходить процесс зарядки конденсатора. Во время зарядки в цепи протекает ток

(11-1)

Следовательно, зарядный ток конденсатора пропорционален скорости изменения напряжения на обкладках конденсатора.

Рис. 129

Рассмотрим процесс изменения напряжения на конденсаторе и тока в цепи во время зарядки конденсатора, т.е. в отрезке времени от момента подключения цепи к источнику постоянного напряжения до момента полной зарядки конденсатора, что соответствует переходному процессу в RC- цепи.

Уравнение электрического состояния согласно второго закона Кирхгофа имеет вид:

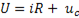. (11-2)

Подставим значение тока в последнее выражение

или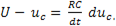

Разделив переменные, получим

.

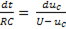Произведение сопротивления и емкости

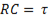(11-3)

называют постоянной времени цепи. Размерность постоянной времени

.

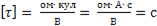Тогда

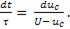(11-4)

Это выражение представляет собой дифференциальное уравнение, отражающее характер изменения напряжения на обкладках конденсатора во время переходного процесса.

Решим это уравнение и построим график зависимости Проинтегрируем уравнение

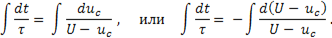
После интегрирования получим

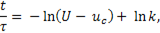
где 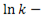постоянная интегрирования.

Значение постоянной интегрирования определим из начальных условий. В момент включения напряжение на конденсаторе равно нулю 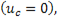следовательно

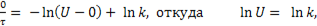т.е.

Это уравнение можно переписать так:

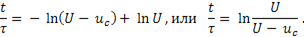
Приведем левую часть равенства под знак логарифма, получим

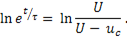
Таким образом,

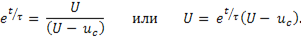
Решая последнее уравнение относительно 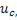найдем

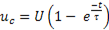. (11-5)

Это выражение показывает, что напряжение на конденсаторе изменяется по экспоненциальному закону.

Теоретически процесс зарядки длится бесконечно долго, так как напряжение 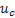станет равным U только при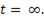

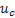Для построения графика определим значения для различных моментов времени:

при

t =

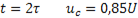
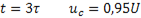
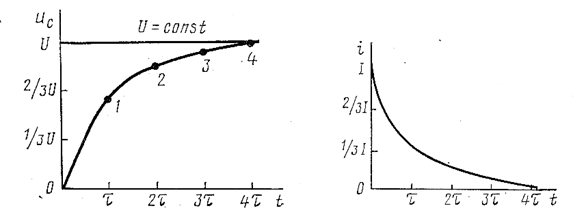
а б

Рис. 130

Из рис. 130а видно, что процесс зарядки практически заканчивается через 4-5 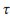. Причем, чем больше 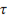, тем больше времени потребуется, чтобы напряжение на конденсаторе достигло значения . Следовательно, по постоянной времени 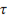можно определять продолжительность переходного процесса. Так как 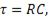то чем больше и С, тем медленнее происходит процесс зарядки конденсатора.

Приложенное напряжение для 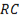- цепи по величине является тем пределом, к которому стремится напряжение на конденсаторе, поэтому чем больше , тем больше _С. Однако величина не влияет на характер кривой 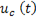, так как характер ее изменения зависит от множителя 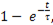т.е. от параметров R и C.

Падение напряжения на резистивном элементе

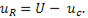
Подставив в это выражение

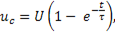
получим

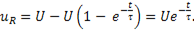(11-6)

Видно, что напряжение на резистивном элементе убывает по экспоненциальному закону.

Ток, проходящий по резистивному элементу, а следовательно, и по цепи (рис.130б),

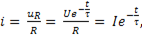(11-7)

где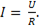

Выражение показывает, что ток в цепи изменяется также по убывающей экспоненте, имея максимум в момент включения цепи, т.к. при а после зарядки конденсатора при

Разрядка конденсатора. На рис. 131 показана схема при разрядке конденсатора на резистивный элемент.

Рис.

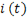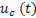Рассмотрим характер изменения и при разрядке конденсатора. Если конденсатор, заряженный до напряжения U, соединить с некоторым резистивным элементом R, то в цепи появится ток, заряды с обкладок начнут убывать и, следовательно, конденсатор будет разряжаться. Ток в цепи определяется скоростью убывания зарядов на обкладках конденсатора: . (11-8)

Знак минус свидетельствует о убывании зарядов на обкладках конденсатора.

Уравнение электрического состояния цепи при разрядке конденсатора имеет вид:

(11-9)

Подставив в это выражение значение тока, получим

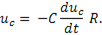
Так как 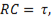то

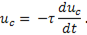
Разделив переменные, определим

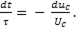(11-10)

Это выражение представляет собой дифференциальное уравнение, отражающее характер изменения напряжения на конденсаторе при разрядке на резистивный элемент. После интегрирования уравнения ( 11-10 ), получим

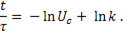
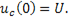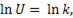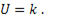Значение постоянной интегрирования определим из начальных условий. В момент включения цепи ( напряжение на конденсаторе Следовательно, откуда т.е. Тогда

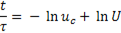
или

=

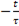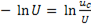
или

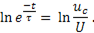
Таким образом

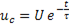. (11-11)

Это выражение показывает, что напряжение на конденсаторе при его разрядке изменяется по закону убывающей экспоненты.

Анализ кривой 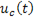(рис. 132 ) подтверждает, что процесс разрядки конденсатора не может происходить мгновенно, и, следовательно, напряжение 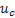уменьшается не скачком, а плавно убывает со временем до нуля.

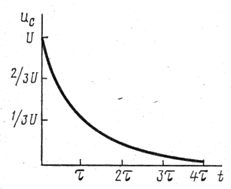
Рис. 132

Переходный процесс поддерживается энергией, накопленной в электрическом поле конденсатора. Запас энергии непрерывно сокращается, а следовательно, уменьшается напряжение на конденсаторе.

Разрядный ток в цепи по закону Ома

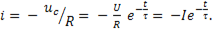(11-12)

График 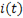при зарядке конденсатора аналогичен (рис. 130б) графику 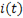при его разрядке.

Саморазрядка конденсатора. Если конденсатор не подключать к резистивному элементу, то с течением времени он разрядится. Это объясняется тем, что практически диэлектрик конденсатора обладает хотя и малой, но отличной от нуля проводимостью, и поэтому конденсатор разряжается через диэлектрическую среду , из которой он изготовлен. Разрядку конденсатора через диэлектрик называют саморазрядкой.

Постоянная времени саморазрядки 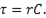Практически саморазрядку можно считать законченной через время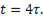

Определим постоянную времени саморазрядки плоского конденсатора. Считая

получим

(11-13)

Таким образом, постоянная времени саморазрядки конденсатора 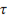зависит только от свойств диэлектрика ( и не зависит от формы конденсатора.