Общие сведения о цепях переменного тока с параллельным соединением дросселя и конденсатора

В цепи переменного тока с параллельным соединением сопротивлений (рис. 2.1) напряжение является общим для всех приемников, а ток в каждой ветви определяется соотношениями

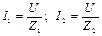. (2.1)

Ток в неразветвленной части цепи определяется как векторная сумма токов отдельных ветвей:

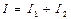. (2.2)

В электрической цепи при параллельном соединении емкостной и индуктивной нагрузок возникает резонанс токов, если равны индуктивные и емкостные проводимости ветвей b_L = b_C.

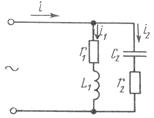
Рис. 2.1. Цепь переменного тока

с параллельным соединением сопротивлений.

Рассмотрим идеальную цепь (рис. 2.2), в которой отсутствует активное сопротивление. При этом токи в индуктивной и емкостной нагрузках равны по величине и противоположны по направлению (I_L = = b_LU; I_C = b_CU). Ток в индуктивной нагрузке отстает от напряжения на 90^о, а в емкостной опережает его на 90^о (I_L = –I_C). Следовательно, при резонансе в рассматриваемой идеальной цепи в подводящих проводах сила тока равна нулю:

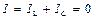. (2.3)

Рис. 2.2. Схема идеальной цепи (а) и векторная диаграмма (б) резонанса токов.

Рассмотрим теперь реальную цепь (рис. 2.3, а). Пусть в ветви с индуктивным сопротивлением имеется и активное сопротивление, что практически соответствует подключению двигателя. В ветви с емкостным сопротивлением сила тока определится по формуле I_C = b_CU. В ветви с индуктивным сопротивлением ток (I₁ = y₁U) состоит из активной составляющей I_a1 = g₁U и индуктивной составляющей I_L1 = –jb₁U (рис. 2.3, б). В режиме резонанса индуктивная составляющая тока I_L1 = = –jb₁U первой ветви равна по значению и противоположна по направлению току второй ветви:

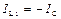. (2.4)

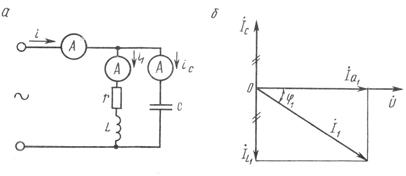
Рис. 2.3. Схема реальной цепи (а) и векторная диаграмма (б) резонанса токов.

Ток в подводящих проводах будет состоять только из активной составляющей тока цепи, т.е.

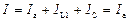. (2.5)

При параллельном резонансе токов реактивные токи замыкаются в параллельном контуре и могут в десятки раз превышать силу тока в подводящих проводах. Поэтому резонанс при параллельном соединении емкостной и индуктивной нагрузок называется резонансом токов. При резонансе токов сдвиг фаз между током и напряжением в цепи равен нулю (cos φ = 1), цепь обладает активным сопротивлением. Векторная диаграмма токов и напряжения при резонансе токов изображена на рис. 2.3, б. Сила тока в подводящих проводах принимает минимальное значение.

Для демонстрации резонанса токов собирают электрическую цепь с параллельным включением батареи конденсаторов и катушки индуктивности (см. рис. 2.2), изменяя емкость батареи конденсаторов при постоянной индуктивности катушки или индуктивность при постоянной емкости, добиваемся минимального показания амперметра, включенного в неразветвленную часть цепи, что соответствует резонансу токов. При этом приложенное напряжение необходимо поддерживать постоянным. Амперметры, включенные в ветви цепи, покажут максимальную силу тока, при этом их показания будут одинаковыми, согласно формуле (2.4).

Режим резонанса токов имеет большое практическое значение в технике сильных токов. При резонансе токов их колебания происходят внутри колебательного контура, внешний источник тока только пополняет потери энергии на активном сопротивлении. В электрических сетях частично происходит обмен энергией между генераторами и потребителями, что загружает сеть реактивными токами и увеличивает потери энергии на нагревание проводов. Чтобы избавить сеть от этих потерь, параллельно приемнику с индуктивным сопротивлением подключают конденсаторы, чем и создают колебательный контур на месте приемника. Параллельное подключение конденсаторов к активно-индуктивной нагрузке повышает коэффициент мощности нагрузки (cos φ).

Коэффициент мощности (cos φ) показывает, какую часть от полной мощности S составляет активная мощность Р. Следовательно, второй составляющей полной мощности является реактивная, которая обозначается буквой Q. Из определения полной мощности (S = IU) как суммы активной (P = IUcos φ) и реактивной можно записать формулу реактивной мощности:

Q = IUsin φ. (2.6)

Реактивная мощность характеризует среднюю скорость накопления и убыли энергии магнитного или электрического поля цепи. Активная мощность определяет скорость преобразования электрической энергии в другие виды энергии (световую, механическую, химическую, внутреннюю).

Коэффициент мощности cos φ имеет большое практическое значение. Увеличение cos φ дает возможность полнее использовать номинальную мощность генератора, трансформатора и другого оборудования. При cos φ = 0,7 активная мощность составляет только 70 % номинальной мощности трансформатора, т.е. все электрооборудование используется на 70 % своей номинальной мощности.

Недогрузка оборудования (генераторов, турбин, трансформаторов) ведет к излишним материальным затратам и экономически невыгодна. Кроме того, недогрузка генераторов, двигателей и трансформаторов приводит к увеличению ненужной реактивной мощности сети.

Увеличение cos φ повышает КПД установки. Следовательно, для передачи одной и той же мощности при большем cos φ нужны провода меньшего сечения, более легкие опоры и другое оборудование линий электропередач, что требует меньшего расхода металла и меньшего капиталовложения на сооружение воздушных линий и установку оборудования.