Общие сведения о трехфазных цепях

Однофазная система неэкономична вследствие несовершенства однофазных электрических машин. Так, например, при одинаковых габаритах, массе активных материалов (стали и меди) и потерях энергии мощность однофазной машины в 1,5 раза меньше мощности трехфазной машины. Поэтому для электрификации используется трехфазная система переменного тока.

Трехфазной системой переменного тока, или просто трехфазной системой, называется цепь или сеть переменного тока, в которой действуют три ЭДС одинаковой частоты, но взаимно смещенные по фазе на одну треть периода. Отдельные цепи, составляющие трехфазную систему, называются фазами.

Если ЭДС во всех трех фазах имеют одинаковую амплитуду и сдвинуты по фазе на одинаковый угол, то такая система называется симметричной.

Обмотки трехфазного генератора соединяют между собой в «звезду» или «треугольник».

При соединении обмоток генератора «звездой» (рис. 3.2, а) концы всех трех фаз соединяют в общую точку О, а к началам подсоединяют провода, отводящие энергию в сеть. Эти три провода называются линейными, а напряжение между любыми двумя линейными провода-ми – линейным напряжением U_л. От общей точки соединения концов трех фаз (от нулевой точки «звезды») может быть отведен четвертый провод, называемый нулевым. Напряжение между любым из трех линейных проводов и нулевым проводом равно напряжению между началом и концом одной фазы, т.е. фазному напряжению U_ф.

Обычно все фазы обмотки генератора выполняются одинаковыми, так что действующие значения ЭДС в фазах равны, т.е. Е_А = Е_В = Е_С. Если в цепь каждой фазы генератора включить нагрузку, то по этим цепям будут проходить токи. В случае одинакового по величине и характеру сопротивления всех трех фаз приемника, т.е. при равномерной нагрузке, токи в фазах будут равны по величине и сдвинуты по фазе относительно своих напряжений на один и тот же угол φ. Как максимальные, так и действующие значения фазных напряжений при равномерной нагрузке равны, т.е. U_A = U_B = U_C. Эти напряжения сдвинуты по фазе на 120^о, как показано на векторной диаграмме (рис. 3.2, б). Напряжения между любыми точками схемы соответствуют векторам между теми же точками. Так, например, напряжение между точками А и О схемы (фазное напряжение U_A) соответствует вектору А–О диаграммы, а напряжение между линейными проводами А и В схемы – вектору линейного напряжения А–В диаграммы. По векторной диаграмме легко установить соотношение между линейным и фазным напряжениями. Из треугольника АОа можно записать следующее соотношение:

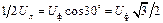, (3.1)

откуда

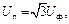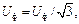или (3.2)

т.е. при соединении обмоток симметричного генератора «звездой» линейное напряжение в 1,73 раза больше фазного.

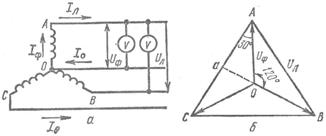
Рис. 3.2. Схемы соединения обмоток трехфазного генератора:

а – соединение «звездой»; б – векторные диаграммы напряжений.

Из схемы (рис. 3.2, а) видно, что при соединении обмоток генератора «звездой» сила тока в линейном проводе равна силе тока в фазах генератора, т.е. I_л = I_ф.

На основании первого закона Кирхгофа сила тока в нулевом проводе равна геометрической сумме силы токов в фазах генератора:

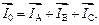(3.3)

При равномерной нагрузке токи в фазах генератора равны между собой и сдвинуты по фазе на одну треть периода. Геометрическая сумма силы токов трех фаз в таком случае равна нулю, т.е. в нулевом проводе тока не будет.

При соединении обмоток генератора «треугольником» (рис. 3.3, а) начало каждой фазы соединяется с концом другой фазы. Таким образом, три фазы генератора образуют замкнутый контур. Так как ЭДС в фазах генератора равны и сдвинуты на одну треть периода по фазе, то геометрически их сумма равна нулю и, следовательно, в замкнутом контуре трехфазной системы, соединенной «треугольником», никакого тока при отсутствии внешней нагрузки не будет.

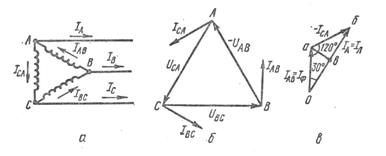
Рис. 3.3. Схема соединения обмоток генератора «треугольником» (а),

векторные диаграммы напряжений и токов в фазах (б) и векторная диаграмма

фазовых и линейных токов (в).

Линейные провода при соединении «треугольником» подключаются к точкам соединения начала одной фазы и конца другой. Напряжение между линейными проводами равно напряжению между началом и концом одной фазы. Таким образом, при соединении обмоток генератора «треугольником» линейное напряжение равно фазному, т.е. U_л = U_ф.

При равномерной нагрузке в фазах обмоток генератора проходят токи равной силы, сдвинутые относительно фазных напряжений на одинаковые углы φ, т.е. I_АВ = I_ВС = I_СА.

Векторная диаграмма фазных напряжений и токов изображена на рис. 3.3, б. Приняв направление фазных и линейных токов за положительное, которое указано на рис. 3.3, а, на основании первого закона Кирхгофа для мгновенных значений токов можно записать следующие выражения:

i_А = i_АВ – i_СА; i_В = i_ВС – i_АВ; i_С = i_СА – i_ВС. (3.4)

Так как токи синусоидальны, заменим алгебраическое вычитание мгновенных значений токов геометрическим вычитанием векторов, изображающих действующие значения токов:

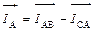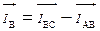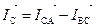; ; . (3.5)

Ток I_А линейного провода А определяется геометрической разностью векторов фазных токов 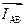и .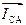

Для построения вектора линейного тока 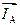изобразим вектор фазного тока 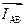(рис. 3.3, в) в виде отрезка Оа, а из точки а построим вектор 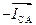(отрезок аб), равный и противоположно направленный вектору 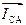(см. рис. 3.3, б). Вектор, соединяющий начало вектора 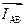(точка О) с концом вектора 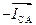(точка б), является вектором линейного тока .

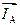Аналогично могут быть построены векторы линейных токов 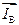и .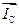

Из векторной диаграммы, показанной на рис. 3.3, в, легко определить соотношение между линейными и фазными токами при соединении обмоток генератора в «треугольник». Из треугольника 0аВ можно записать:

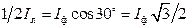, (3.6)

откуда I_л = 1,73 I_ф, т.е. при соединении обмоток генератора в «треугольник» линейный ток в 1,73 раза больше фазного (при равномерной нагрузке).

Несимметричная нагрузка включается в трехфазную сеть «звездой» с нулевым проводом. При этом каждая фаза трехфазной цепи независима от других фаз. Напряжения на фазных нагрузках всех трех фаз одинаковы, несмотря на разные величины фазных нагрузок. Изменение фазной нагрузки одной фазы вызывает изменение силы тока в данной фазе, которая влияет на силу тока только в нулевом проводе и не влияет на силу тока в других фазах. Для того чтобы нулевой провод не мог отключаться, на нем не ставят предохранителей. Несимметричной нагрузкой трехфазной цепи является нагрузка источников освещения и приемников бытового обслуживания (электроплиты, холодильники, телевизоры и т.д.).

Несимметричную нагрузку нельзя подключать в трехфазную сеть «звездой» без нулевого провода. Если это сделать, произойдет перераспределение напряжений по фазам. На фазах, имеющих большее сопротивление, напряжение будет больше номинального фазного напряжения, и приемники перегреются и даже могут сгореть. На фазах, имеющих меньшее сопротивление, напряжение будет меньше номинального, и приемники получат меньшую мощность.

Например, в трехфазной сети с линейным напряжением 380 В при подключении приемников «звездой» без нулевого провода в фазе В включена одна лампа, в фазе С – девять таких же ламп, а фаза А не имеет приемника, что соответствует ее обрыву. При этом приемники фаз В и С окажутся подключенными последовательно к линейному напряжению сети, которое распределится по фазам прямо пропорционально сопротивлениям. Следовательно, приемник фазы В будет под напряжением 342 В (380 – 380 ∙ 1/10), а приемник фазы С – под напряжением 38 В при номинальном фазном напряжении 220 В (380 – ‑ 380 ∙ ^.9/10).

При равенстве фазных сопротивлений фазы В и С окажутся под следующими фазными напряжениями: U^/_В = U^/_С = 190 В; U^/_А = 328,7 В (рис. 3.4, а).

при несимметричной нагрузке трехфазной сети без нулевого провода потенциал узловой точки О^/ нагрузки не равен потенциалу узловой точки О фаз генератора, т.е. произойдет смещение нейтрали и возникнет напряжение смещения нейтрали U_N.

По закону Ома для каждой фазы цепи имеем:

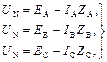(3.7)

где роль ЭДС играют фазные напряжения генератора U_A, U_B, U_C (в симметричной системе равные по величине и сдвинутые по фазе на 120^о), а I_AZ_A = U^/_A; I_ВZ_В = U^/_В; I_СZ_С = U^/_С есть падение напряжения на фазных нагрузках. Следовательно, фазные напряжения нагрузки выразятся уравнениями: U^/_A = U_A – U_N; U^/_B = U_B – U_N; U^/_C = U_C – U_N.

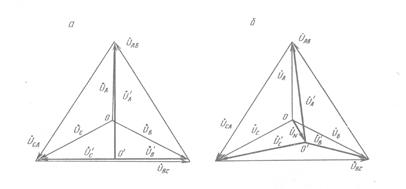
Рис. 3.4. Векторные диаграммы линейных и фазных напряжений

при несимметричной нагрузке трехфазной цепи без нулевого провода.

Топографическая диаграмма фазных и линейных напряжений будет иметь вид, показанный на рис. 3.4, б. Для определения напряжения смещения нейтрали U_N воспользуемся равенством (3.7) и запишем его в следующем виде:

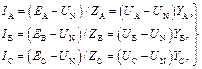
где Y_A, Y_B, Y_C – комплексные проводимости фазных нагрузок.

Так как для симметричной трехфазной сети без нулевого провода I_A + I_B + I_C = 0, то (U_A – U_N)Y_A + (U_В – U_N)Y_В + (U_С – U_N)Y_С = 0, откуда

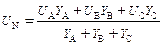. (3.8)

Определив напряжение смещения нейтрали U_N по формуле (3.8), можно найти фазные токи при неравномерной нагрузке.