Методы расчета тяговой силы электромагнита.

7.2.1. Графический метод. Для расчета должно быть задано семейство магнитных характеристик 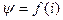(рис. 83) для нескольких положений якоря в диапазоне хода от начального зазора 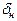до конечного и установившееся значение тока в катушке. Эти зависимости определяются путем расчета магнитной цепи электромагнита.

На интервале движения якоря 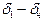работа, совершенная электромагнитом, будет равна 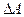. Обозначим величину перемещения

.

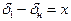Тогда, 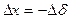, так как .

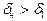Определим среднюю тяговую силу на этом интервале

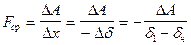(206)

или 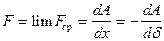. (207)

Рис. 83. Семейство магнитных Знак (–) показывает, что тяговая сила

характеристик действует в сторону уменьшения воздушного зазора.

Поскольку 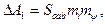то 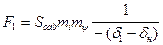. (208)

На интервале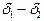

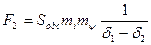. (209)

На следующих интервалах решают аналогично. Определив тяговые силы на всех интервалах от 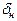до , строят статическую тяговую характеристику электромагнита.

Статической тяговой характеристикой называется зависимость тяговой силы электромагнита от воздушного зазора при неизменном токе в катушке. Считая, что тяговая сила на границах интервала изменяется скачком, а в пределах интервала она остается постоянной, строим ступенчатый график 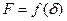(рис. 84).

Рис. 84. Тяговая характеристика Затем, через точки, соответствующие средним воздушным зазорам на каждом интервале

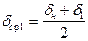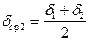, и т.д.,

проводим плавную линию, которая и будет статической тяговой характеристикой.

7.2.2. Расчет тяговой силы для ненасыщенных электромагнитов.

Когда магнитная система электромагнита не насыщена, магнитные характеристики имеют линейный характер (рис. 85).

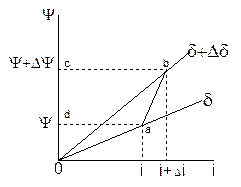
Работа, совершенная электромагнитом при перемещении якоря от зазора 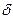до 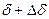будет равна:

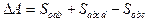, где

.

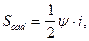
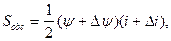
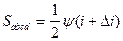Подставляя значения S в выражение

Рис. 85. К расчету тяговой силы для 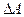и делая преобразования, по-

лучим:

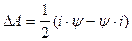. (210)

Тяговая сила будет равна:

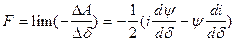. (211)

а) Если система работает при постоянной намагничивающей силе (т.е. 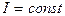), то работа определяется по выражению:

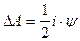, т.е. .

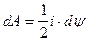Если учесть, что 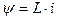и 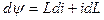, тогда

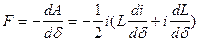. (212)

Так как 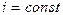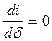, тогда .

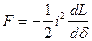Учитывая, что 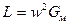и 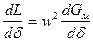, тогда получим:

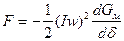Н, (213)

где 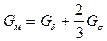. (214)

б) Если система работает при постоянном потокосцеплении (т.е. 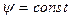), то

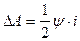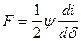, . (215)

Так как 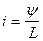, то 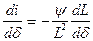. Подставляя в выражение для силы, получим

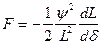. (216)

Учитывая, что 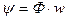, 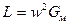и 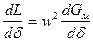, получим

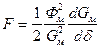. (217)

Так как 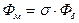, то

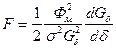. (218)

Если не учитывать потери МДС в стали (т.е. R_мст = 0), то

, .

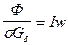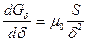Тогда,

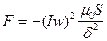. (219)

7.2.3. Расчет тяговой силы электромагнита по формуле Максвелла. Формула Максвелла, устанавливающая связь между значением тяговой силы и величиной магнитного потока в воздушном зазоре, а также размерами полюса электромагнита, имеет вид

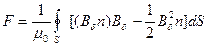, (220)

где 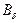– вектор индукции в воздушном зазоре на поверхности полюса; n – единичная нормаль к поверхности полюса; S – площадь поверхности полюса.

Формула Максвелла учитывает как неравномерное распределение потока в воздушном зазоре, так и возможность неперпендикулярного направление вектора индукции к поверхности полюса.

Поверхность полюса S является поверхностью раздела двух сред с различной магнитной проницаемостью ( 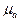и 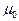). Если 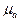>> 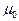, то угол между нормалью и вектором индукции в среде с магнитной проницаемостью 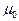будет небольшим, а потому, с достаточной точностью можно принять, что вектор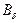 совпадает с нормалью n. В этом случае формула Максвелла приобретает более простой вид

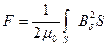. (221)

Если индукция постоянна по всей поверхности полюса, т.е. магнитный поток равномерно распределен по воздушному зазору, то в выражении (223) интеграл по площадке S, можно опустить и формула Максвелла принимает вид

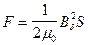Н. (222)

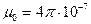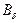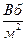Подставляя Г/м, – , S – 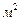получим

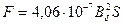кгс. (223)

Равномерное распределение магнитного потока в воздушном зазоре может быть принято лишь для некоторых частных случаев. Например, при цилиндрических полюсах, когда воздушный зазор очень мал и магнитная цепь не насыщена, потоки выпучивания малы и ими можно пренебречь.

В большинстве случаев условие равномерности распределения магнитного потока в зазоре не соблюдается. Поэтому формулой Максвелла в упрощенном виде (222) и (223) целесообразно пользоваться для ориентировочных расчетов.