Общие советы при построении графиков
Заглавие графика в книгах и журналах помещается внизу, а в диаграммах, не предназначенных для печати, например, в настенных диаграммах, целесообразнее писать заголовок сверху.
При построении графиков рекомендуются следующие правила:
1. Общая структура графиков должна предполагать чтение слева направо.
2. Когда используется возможность изображать количества линейных величин с помощью, например, площадей или объемов, вероятнее всего, что их не удастся верно истолковать.
3. Вертикальную шкалу для кривой, независимо от ее назначения, следует выбрать так, чтобы на рисунке оказалась нулевая отметка.
4. Если нулевая линия вертикальной шкалы окажется не перпендикулярной по отношению к графику, то нулевая линия должна быть показана с помощью горизонтальной оси.
5. Нулевые линии шкал для кривой следует резко отграничивать от других координатных линий.
6. Для кривых, которые имеют шкалу, изображающую проценты, как правило, желательно выделить каким-то образом линию 100 % или другие линии, используемые в качестве основы для сравнения.
7. Когда шкала относится к датам, а представляемый период является неполным, лучше не выделять первые и последние ординаты, так как подобная диаграмма не отмечает начало или конец времени.
8. Когда кривые рисуются в логарифмических координатах, ограничительные линии должны находиться на том же уровне – кратном десяти – на логарифмических шкалах.
9. Рекомендуется показывать не больше координатных линий, чем это необходимо, чтобы облегчить чтение диаграммы.
10. Кривые линии диаграммы должны резко отличаться от прямых.
11. Для кривых, характеризующих группы наблюдений, рекомендуется по возможности ясно указывать на диаграмме все кривые, представляющие отдельные наблюдения.
12. Горизонтальную шкалу для кривых следует читать, как правило, слева направо, а вертикальную – снизу вверх.
13. Цифры на шкалах следует располагать слева и снизу или вдоль соответствующих осей.
14. Часто желательно включать в график цифровые данные или изображаемые формулы.
15. Если цифровые данные не попали на график, желательно привести данные в таблице, сопровождающей график.
16. Все обозначения и цифры для удобства чтения следует располагать от основания как начала или с правого края как начала.
17. Наименования следует делать возможно яснее и полнее. Если это требуется, необходимо дополнительно вводить подзаголовки или пояснения.
была как можно меньше, то есть чтобы сумма квадратов ошибок оценки была минимальна.
Домашнее задание № 1
Вам необходимо, используя таблицу 3.1, определить N-ый процентиль
| № | ПІБ | Процентиль |
| Вожжов Никита Вячеславович | ||
| Глущенко Никита Сергеевич | ||
| Дымченко Владислав Андреевич | ||
| Загоруйко Данил Евгеньевич | ||
| Ковалёв Вячеслав Анатольевич | ||
| Михайленко Владислав Игоревич | ||
| Романов Вячеслав Игоревич | ||
| Сергеев Даниил Юрьевич | ||
| Усик Богдан Константинович | ||
| Мастеровенко Анастасия | ||
| Михайлова Алина | ||
| Толмачева Елена | ||
| Трунаев Андрей |
ГИПОТЕЗА И ВЫВОД. ОПРЕДЕЛЕНИЕ ОБЪЕМА ВЫБОРКИ
Вывод – это процесс рассуждения от «нечто» ко «всему» (от частного к общему). Обоснованность вывода будет зависеть от того, при какой представительности «нечто» характеризует «всё». Как получить представительную выборку? Один из методов – это простой случайный выбор (часто прилагательное «простой» опускается).
Простой случайный выбор – это процесс отбора наблюдений из большой группы таким образом, чтобы каждое наблюдение имело равную и независимую вероятность быть выбранным. Многочисленная группа (конечная или бесконечная) называется совокупностью или генеральной совокупностью; меньшая – выборкой из совокупности. Если выбор случайный, то процесс отбора наблюдений будет обеспечивать каждому наблюдению в совокупности одинаковый шанс попасть в выборку. Кроме того, если выбор действительно является случайным, то результат одного выбора не зависит от результата любого другого.
Условие равновероятности в определении случайного выбора предполагает, что на каждой стадии процесса выбора все оставшиеся элементы имеют одинаковую вероятность быть выбранными.
Существуют многочисленные способы приблизительного обеспечения равновероятности. Наилучшим методом получения случайных выборок является применение таблицы случайных чисел.
Ещё раз подчеркнём, что если выборка из n наблюдений является случайной, то независимо от того, какими были первые n1 выборов, вероятность выбора любого возможного наблюдения при (n1 + 1) равна 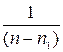 .
.
Для определения объёма выборки педагогического признака (неуспеваемость, текучесть кадров, опоздания) в общей совокупности исследуемых объектов можно воспользоваться формулой
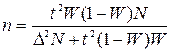 ,
,
где n – объём выборки,
N – объём генеральной совокупности,
W – выборочная доля исследуемого явления,
Δ – предельная ошибка выборки (отклонения выборочной доли W от генеральной р) с определённой вероятностью, которая обусловлена величиной коэффициента значимости.
При t = 2 вероятность того или иного отклонения выборочной доли исследуемого признака от генеральной (р = W 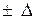 ) равняется
) равняется 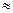 5 %. (приложение 3)
5 %. (приложение 3)
При отсутствии сведений о выборочной доле при определении численного значения n обычно принимают значение максимального выражения W(1 – W) (max = 0,25) (при W = 1 – W = 0,5)
Пример.
Пусть N = 90 000 W(1 – W) = 0,25 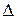 = 0,05 t = 2
= 0,05 t = 2
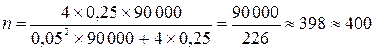
Пусть N = 30 000 W(1 – W) = 0,25 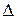 = 0,02 t = 2,327
= 0,02 t = 2,327
N = 30 000 W(1 – W) = 0,25 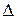 = 0,05 t = 1,96
= 0,05 t = 1,96 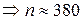
N = 120 W(1 – W) = 0,25 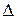 = 0,05 t = 1,96
= 0,05 t = 1,96 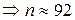
Следует подчеркнуть, что понятие случайной выборки является основным в математической статистике. Но не всякий отбор наудачу даёт выборку в том смысле, как это мы условились понимать выше. Мы можем, например, отобрать ряд чисел, взятых наудачу, но не осуществить при этом случайный отбор элементов в данной совокупности потому, что, как показывает опыт, мы склонны бессознательно оказывать предпочтение одним числам перед другими, например четным перед нечётными или малым по сравнению с большими и т.д.
Случайность выборки, гарантирующая полную беспристрастность отбора, должна проявляться, прежде всего, в невозможности по полученным в выборке номерам строить какой-либо прогноз в отношении следующих отбираемых номеров.
Выборка с возвращением будет случайной лишь при том условии, что каждый элемент рассматриваемой совокупности имеет равную со всеми остальными элементами вероятность оказаться в выборке при каждом очередном отборе.
Несмотря на кажущуюся простоту этих интуитивно очевидных требований, предъявляемых к выборке, их осуществление на практике оказывается не таким уж простым.
В настоящее время случайный отбор осуществляется обычно при помощи специальных таблиц так называемых «случайных чисел».
В таблице 2.1.2 приводится выдержка из «Таблицы случайных чисел» М. Кадырова, Ташкент, изд. САГУ, 1936, стр. 4 (верхняя половина страницы). Четырёхзначные числа в этой таблице сгруппированы в группы по пять чисел, расположенных столбиком, причём таких столбиков в каждом столбце страницы содержится десять и столбцов на странице также десять. Таким образом, на каждой странице помещается 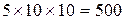 четырёхзначных чисел. Способ составления этих таблиц гарантирует равновероятность цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 на каждом месте каждого четырёхзначного числа таблицы. Таблица М. Кадырова на самом деле не удовлетворяет условию равновероятности, что можно обнаружить путём довольно кропотливого статистического исследования (см. Л. М. Большев. О случайных числах М.Кадырова, Теория вероятности и её применения 9:1 (1964)).
четырёхзначных чисел. Способ составления этих таблиц гарантирует равновероятность цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 на каждом месте каждого четырёхзначного числа таблицы. Таблица М. Кадырова на самом деле не удовлетворяет условию равновероятности, что можно обнаружить путём довольно кропотливого статистического исследования (см. Л. М. Большев. О случайных числах М.Кадырова, Теория вероятности и её применения 9:1 (1964)).
Рассмотрим пример использования этой таблицы. Пусть совокупность состоит из 543 элементов (объектов) и нам нужно отобрать из неё случайную выборку с возвращением из 12 элементов. Прежде всего мы должны пронумеровать все объекты нашей совокупности, начиная с номера 000 и кончая номером 542. Затем мы используем таблицу случайных чисел. Откроем наугад страницу и выберем на ней наугад столбец, а в нём, также наугад, число, три первых знака которого составят номер первого объекта, попавшего в совокупность. Остальные 11 номеров объектов мы возьмём, следуя какому-нибудь определённому заранее установленному правилу, например: 1) подряд вниз по столбцу, 2) подряд вверх по столбцу, 3) подряд вправо по столбцам, 4) подряд влево по столбцам и т.д. Любое из этих правил даёт нужный результат. Пусть мы взяли число 2157, второе сверху в первом столбике третьего столбца, решив применить первое правило. Тогда мы получим выборку из следующих номеров: 215, 250, 062, 381, 164, 084, 438, 050, 486, 501, 364, 031. Идя подряд сверху по столбцу, мы пропускали числа, первые три знака которых дают число, большее 542. Отобранные нами 12 номеров позволяют взять 12 объектов из нашей совокупности, имеющих те же порядковые номера.
Если нужно отобрать выборку без возвращения, то мы пропускаем также числа, дающие номера, уже попавшие в выборку. В нашем примере совпавших номеров нет, а потому в этом частном случае выборка с возвращением и выборка без возвращения содержали бы одни и те же объекты.
Дата добавления: 2020-10-01; просмотров: 655;











