Обработка результатов исследования скважин со снятием кривой восстановления давления на забое при эксплуатации трещиноватых пластов
Методика основана на соотношениях 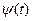 для неустановившихся процессов в стволе скважины после изменения режима ее работы, соответствующих начальным и более поздним периодам изменения давления:
для неустановившихся процессов в стволе скважины после изменения режима ее работы, соответствующих начальным и более поздним периодам изменения давления:
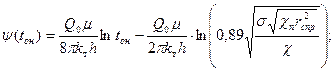 (7.43)
(7.43)
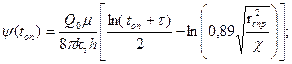 (7.44)
(7.44)
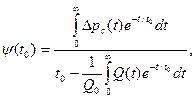 (7.45)
(7.45)
где kт — проницаемость трещиноватого пласта;
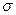 — удельная поверхность трещин
— удельная поверхность трещин 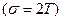 ;
;
Т — объемная плотность трещин;
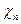 — пьезопроводность пористой среды.
— пьезопроводность пористой среды.
Время регистрации показателей после изменения режима работы скважины должно быть не менее 4—8 ч.
В качестве исходных данных для расчета выбирают значения давления (и дебита) в моменты времени ti, составляющие (начиная с t2) геометрическую прогрессию со знаменателем 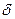 , не превышающим двух. Удобнее принять
, не превышающим двух. Удобнее принять 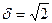 .
.
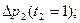
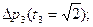
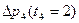 . . .;
. . .; 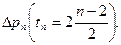
Значения давлений, не совпадающие для указанных моментов времени с замеренными, находятся линейным интегрированием между двумя имеющимися точками.
Далее определяются вспомогательные функции Si.
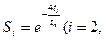 3, . . ., n-1); Sn = 0. (7.46)
3, . . ., n-1); Sn = 0. (7.46)
В координатах р, S проводятся прямые 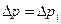 и
и 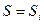 до их попарного пересечения.
до их попарного пересечения.
Через п указанных точек пересечения в точку (0,1) проводится кривая 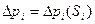 , которая соответствует величине
, которая соответствует величине 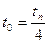 . Через (п—1) ближайшие к построенной кривой узловые точки и точку (0,1) проводится кривая, соответствующая
. Через (п—1) ближайшие к построенной кривой узловые точки и точку (0,1) проводится кривая, соответствующая 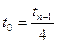 , и т. д. до кривой, соответствующее значение
, и т. д. до кривой, соответствующее значение 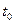 для которой будет
для которой будет 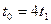 .
.
С помощью планиметра или по формуле Симпсона определяются площади, ограниченные каждой из построенных кривых и осями координат. Произведение величин этих пло-щадей на соответствующее значение 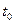 дает искомую величину интеграла в формуле(7.45).
дает искомую величину интеграла в формуле(7.45).
Кривая восстановления давления строится в координатах 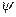 ,
, 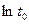 .
.
Если кривая имеет начальный прямолинейный участок, то определяется ее уклон к оси абсцисс ( 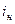 ) и отрезок, отсекаемый на оси ординат (Вн). Выбирая два достаточно больших значения t0, вычисляются
) и отрезок, отсекаемый на оси ординат (Вн). Выбирая два достаточно больших значения t0, вычисляются
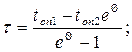
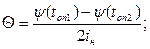 (7.47)
(7.47)
и кривая строится в координатах 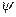 ,
, 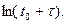
Если кривая 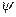 ,
, 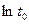 имеет асимптотический прямолинейный участок с уклоном коси абсцисс (
имеет асимптотический прямолинейный участок с уклоном коси абсцисс ( 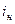 ), то, определяя Вн и сопоставляя с выражением (7.44), получим
), то, определяя Вн и сопоставляя с выражением (7.44), получим
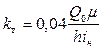 ; (7.48)
; (7.48)
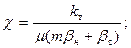 (7. 49)
(7. 49)
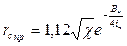 ; (7.50)
; (7.50)
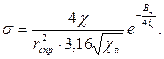 (7.51)
(7.51)
Дата добавления: 2016-07-22; просмотров: 1608;











