Погашение потребительского кредита изменяющимися суммами - правило «78».
При погашении кредита иногда возникает необходимость определить сумму, идущую на погашение основного долга, и суммы процентных платежей. Такая ситуация возможна, например, при досрочном погашении долга. Для решения этого вопроса можно воспользоваться правилом «78».
Для того чтобы объяснить происхождение названия этого правила, рассмотрим следующий пример:
Кредит предоставлен на 1 год с ежемесячным погашением. Сумма порядковых номеров месяцев года равна: 1+2+3+4+5+6+7+8+9+10+11+12=78. В соответствии с этим правилом уплата при первом платеже составит величину 12/78 общей начисляемой суммы процентов. А оставшуюся часть платежа пойдет на уплату основного долга. При втором платеже: на оплату процентов идет 11/78 общей суммы начисления процентов, а оставшаяся часть погашает основной долг и т.д.
В общем случае знаменатель этих дробей можно определить по формуле: 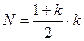 , где к – количество платежей в году.
, где к – количество платежей в году.
После определения знаменателя, составляют следующую последовательность дробей: 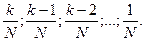 Величина каждой из этих дробей, в сумме составляющих единицу, показывает какая часть общей начисляемой суммы процентов идет на уплату процентов. Оставшаяся часть платежа идет на погашение основного долга.
Величина каждой из этих дробей, в сумме составляющих единицу, показывает какая часть общей начисляемой суммы процентов идет на уплату процентов. Оставшаяся часть платежа идет на погашение основного долга.
Схема с убывающей величиной процентной платы соответствует логике ссудно-заемных операций. Поскольку с течением времени сумма основного долга снижается, то и сумма процентов, начисляемых на непогашенный остаток долга, должна снижаться. Эта схема страхует кредитора на случай досрочного погашения долга, если эта возможность предусмотрена кредитным договором. При досрочном погашении долга заемщик понесет определенный убыток, т.к. большая часть процентов он уже заплатил в начале срока кредитования.
Пример. Кредит в сумме 15000 рублей выдан на 2 года под 20% годовых. Проценты простые. Погашение задолженности производится ежемесячными платежами. Составить план погашения задолженности.
Решение: 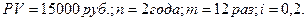
Наращенная сумма долга в конце периода составит 
Сумма начисленных процентов D = 21 000 – 15 000 = 6 000 рублей. Количество платежей в году - 12, следовательно, за весь рассматриваемый период количество платежей к = 12·2 = 24. Определим значение знаменателя 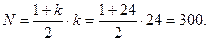
Определим величину разового платежа: 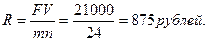
В соответствии с правилом «78» уплата при первом платеже составит величину 24/300 общей начисляемой суммы процентов (6 000 рублей). Оставшаяся часть платежа пойдет на уплату основного долга. При втором платеже на оплату процентов пойдет 23/300 общей суммы начисленных процентов, а оставшаяся часть будет направлена на погашен6ие основного долга и т.д.
В соответствие с этим получим следующий план погашения долга:
(руб.)
| Остаток основного долга на начало месяца | 
| Сумма погашения процентных платежей | Сумма погашения основного долга |
| 24/300 | |||
| 23/300 | |||
| 22/300 | |||
| 21/300 | |||
| 20/300 | |||
| 19/300 | |||
| 18/300 | |||
| 17/300 | |||
| 16/300 | |||
| 15/300 | |||
| 14/300 | |||
| 13/300 | |||
| 12/300 | |||
| 11/300 | |||
| 10/300 | |||
| 9/300 | |||
| 8/300 | |||
| 7/300 | |||
| 6/300 | |||
| 5/300 | |||
| 4/300 | |||
| 3/300 | |||
| 2/300 | |||
| 1/300 | |||
| Σ | 1,000 |
Дата добавления: 2016-07-22; просмотров: 7517;











