С учетом покупательной способности
Реально наращенная сумма денег может быть рассчитана на основе наращения первоначальной суммы денег 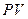 , скорректированной с учетом инфляции. При этом формулы наращения выбирают разные, в зависимости от применяемого процента (простой или сложный), а инфляционное влияние следует оценивать по сложному проценту, т.к. обесцениваются уже обесцененные деньги. Так, если наращение производится по простым процентам, то процесс наращения при наличии инфляции описывается формулой:
, скорректированной с учетом инфляции. При этом формулы наращения выбирают разные, в зависимости от применяемого процента (простой или сложный), а инфляционное влияние следует оценивать по сложному проценту, т.к. обесцениваются уже обесцененные деньги. Так, если наращение производится по простым процентам, то процесс наращения при наличии инфляции описывается формулой: 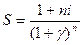 . (5.8)
. (5.8)
Если наращение производится по сложным процентам – по формуле:
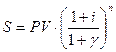 (5.9)
(5.9)
Где 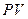 - первоначальная сумма денег, размещенная на вкладе;
- первоначальная сумма денег, размещенная на вкладе;
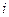 - годовая декурсивная ставка процента по вкладу;
- годовая декурсивная ставка процента по вкладу;
γ - средний годовой темп инфляции;
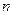 - срок вклада.
- срок вклада.
Формула 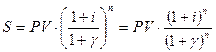 , характеризует процесс наращения в условиях инфляции: ставка доходности является фактором роста денег и находится в числителе, а показатель инфляции является фактором их обесценивания и находится в знаменателе.
, характеризует процесс наращения в условиях инфляции: ставка доходности является фактором роста денег и находится в числителе, а показатель инфляции является фактором их обесценивания и находится в знаменателе.
При сравнении годовой ставки процента по вкладу и среднего годового темпа инфляции возможны три случая:
1). 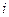 > γ , тогда S >
> γ , тогда S > 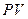 , т.е. только часть наращенной суммы денег «поглощается» инфляцией. Это наиболее оптимальный результат.
, т.е. только часть наращенной суммы денег «поглощается» инфляцией. Это наиболее оптимальный результат.
Темпы наращения денег по ставке процента опередили темп их обесценивания, в связи с этим, первоначальная сумма денег сохранила свою покупательную способность, и даже был получен некоторый прирост денег по вкладу.
2). 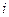 = γ, тогда S =
= γ, тогда S = 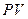 , т.е. все наращение по вкладу «поглощено» инфляцией. Следовательно, роста реальной суммы нет. В этом случае ставка процента по вкладу позволила лишь сохранить покупательную способность первоначальной суммы вклада от инфляции.
, т.е. все наращение по вкладу «поглощено» инфляцией. Следовательно, роста реальной суммы нет. В этом случае ставка процента по вкладу позволила лишь сохранить покупательную способность первоначальной суммы вклада от инфляции.
3). 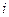 < γ , тогда S <
< γ , тогда S < 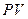 . Т.е. инфляция «поглотила» все наращение и даже часть первоначальной суммы денег, размещенной на вкладе. Такое положение называют «эрозией капитала». В этом случае темпы роста инфляции опередили темпы роста наращения денег по ставке процента. Это наихудший результат, при котором не удается спасти вложенные деньги от обесценивания в условиях инфляции.
. Т.е. инфляция «поглотила» все наращение и даже часть первоначальной суммы денег, размещенной на вкладе. Такое положение называют «эрозией капитала». В этом случае темпы роста инфляции опередили темпы роста наращения денег по ставке процента. Это наихудший результат, при котором не удается спасти вложенные деньги от обесценивания в условиях инфляции.
Пример. Первоначальная сумма вклада составляет 6000 руб. Вклад размещен на 3 года под 4,5% годовых. В течение срока вклада ожидается средний годовой темп инфляции на уровне 7%. Требуется определить наращенную сумму денег с учетом инфляции.
Решение: 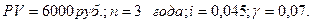
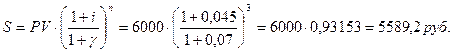
Т.о. инфляция «поглотила» все наращение и даже часть первоначальной суммы вклада. Данная финансовая операция не позволила сохранить деньги от инфляции. По истечении срока вкладчик по покупательной способности получил сумму денег меньшую, чем та, которую он разместил на вкладе. Иначе говоря, произошла «эрозия капитала». Это стало возможно потому, что среднегодовой темп роста инфляции опередил наращение денег по декурсивной ставке процента.
Пример. Ежемесячный уровень инфляции составляет 7% (по отношению к предыдущему месяцу). Исчислить реально наращенную стоимость вклада в 200 тыс. руб., хранящегося на счете до востребования в сбербанке в течение 7 месяцев по ставке 10% годовых. Проценты простые.
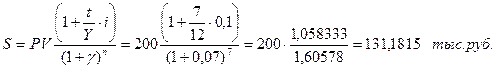
Отметим, что в проектном анализе часто не вычисляют S, довольствуются сравнением 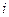 и γ путем вычисления
и γ путем вычисления 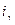 – реальной процентной ставки или нетто-ставки - ставки доходности уменьшенной под влиянием инфляции. Ее находят из соотношения:
– реальной процентной ставки или нетто-ставки - ставки доходности уменьшенной под влиянием инфляции. Ее находят из соотношения:
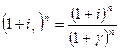
Выразив из этого равенства 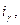 получим:
получим: 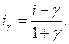 (5.10)
(5.10)
Пример. Определить целесообразность помещения средств на год под 20% годовых, если прогнозируемый уровень инфляции 15%.
Решение: 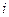 = 0,2; γ = 0,15.
= 0,2; γ = 0,15.
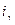 =
= 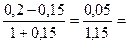 0,0435
0,0435
Реальная положительная ставка - 4,35%, т.е. реальный доход по операции будет 4,35% от каждой единицы вложенных средств, обесцененной за год на 13% ( 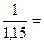 0,87 или 87% 100-87=13%)
0,87 или 87% 100-87=13%)
Дата добавления: 2016-07-22; просмотров: 3220;











