Модели роста популяций

В экологии существует несколько моделей роста популяций (т.е. закономерностей изменения численности популяции при ее росте «от нуля»), главные из них – экспоненциальная и логистическая.

О тенденции быстрого неограниченного увеличения числа особей вида знал К. Линней. Однако представления об экспоненциальном росте популяций в начале прошлого столетия сформулировал Т. Мальтус: количество особей в популяции увеличивается в геометрической прогрессии. В качестве примера Мальтус привел гипотетический рост народонаселения страны при условии естественной смертности (при отсутствии эпидемий и войн). Представления о способности любой популяции к экспоненциальному росту является краеугольным камнем популяционной экологии. П.В. Турчин (2002) считает экспоненциальный рост главным законом экологии, близким по значению к закону Ньютона в физике.

Модель экспоненциального роста описывается J‑образной кривой: в условиях постоянного поступления ресурсов скорость роста популяции увеличивается и кривая взмывает вверх (рис. 15). Модель может быть описана уравнением:

N_t = N₀ е^rt,

в котором N_t – численность популяции через очередной промежуток времени (t),

N₀ – исходная численность,

е – основание натурального логарифма,

r – коэффициент размножения (репродуктивный потенциал, разность относительной рождаемости и относительной смертности, т.е. число родившихся или умерших особей отнесенное к числу особей популяции в начале промежутка времени t).

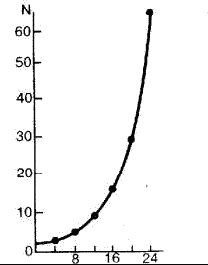
Рис. 15. Экспоненциальная модель роста численности популяции одноклеточного организма, делящегося каждые 4 часа.

Чтобы рост популяции соответствовал этой модели, величина коэффициента r должен быть постоянной, т.е. должно быть постоянным среднее количество потомков на одну особь (если r = 0, т.е. рождаемость равна смертности, то численность популяции не растет).

В зависимости от величины r увеличение численности особей может быть быстрым и достаточно медленным. Ч. Дарвин рассчитал потенциальные возможности роста популяций разных организмов при реализации экспоненциальной модели. По его оценкам, число потомков одной пары слонов – животных, размножающихся чрезвычайно медленно, – через 750 лет достигнет 19 млн. Если же обратиться к организмам, живущим не так долго и размножающимся более быстро, то цифры будут еще более впечатляющими. У бактерий, которые делятся каждые 20 минут, из одной бактериальной клетки через 36 часов может образоваться биомасса, которая покроет весь земной шар слоем толщиной 30 см, а еще через 2 часа – слоем в 2 м.

«Поскольку ни бактерии, ни слоны не покрывают землю сплошным слоем, очевидно, что на самом деле в природе экспоненциальный рост популяций организмов или не происходит вообще, или же происходит, но в течение непродолжительного времени, сменяясь затем спадом численности или выходом ее на стационарный уровень» (Гиляров, 1990, с. 77).

В природе экспоненциальный рост численности популяций наблюдается в сравнительно кратковременные периоды их жизни при особо благоприятных условиях, когда постоянно пополняются ресурсы. Так в озерах умеренных широт весной после таяния льда в приповерхностном слое воды содержится много биогенных элементов. По этой причине после прогревания воды здесь наблюдается быстрый рост численности диатомовых и зеленых водорослей. Однако он также быстро прекращается, когда эти ресурсы оказываются израсходоваными и, кроме того, зоопланктон начнет активно выедать водоросли (т.е. за счет регулирования плотности популяций «снизу» и «сверху»).

Пример экспоненциального роста популяции – история интродукции северного оленя на острова. Так от 25 особей (4 самца и 21 самка), завезенных в 1911 г. на остров Святого Павла (Берингово море), к 1938 г. сформировалась популяция из 2000 оленей. Однако затем последовал спад численности, и к 1950 г. сохранилось всего 8 особей. Причина краха популяции – нарушение отношений «растение – фитофаг» (см. 8.3) ввиду отсутствия в пищевой цепи третьего звена – хищника.

Логистическая модель роста популяций, описываемая S‑образной кривой (медленный рост – быстрый рост – медленный рост, рис. 16), была предложена также в начале 19‑го столетия бельгийским математиком П.‑Ф. Ферхюльстом, а затем уже в 20‑е гг. нашего столетия переоткрыта американскими учеными Р. Перлем и Л. Ридом. П.В. Турчин считает эту модель отражением закона «самоограничения роста любой популяции».

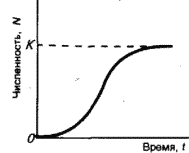
Рис. 16. Логистическая модель роста популяции. К – предельная численность

Причины замедления роста популяции могут быть самыми различными: выедание ресурсов, влияние эффекта скученности (у грызунов при этом снижается интенсивность репродуктивного процесса), отравление местообитания прижизненными выделениями, выедание популяции хищниками и т.д.

Тем не менее и эта кривая является идеализацией, так как крайне редко проявляется в природе. Очень часто после того, как рост популяции выйдет на плато (достигнет предела К, соответствующего количеству ресурсов), происходит внезапное уменьшение ее численности, а потом популяция вновь быстро растет. Таким образом, ее динамика оказывается состоящей из повторяющихся логистических циклов.

Такая циклическая динамика наблюдается, например, в популяциях тундровых леммингов, которые питаются мхами и лишайниками. Они продолжают активную жизнедеятельность под снегом и выедают свою кормовую базу настолько, что прекращают размножаться, а затем начинают умирать от бескормицы. После того, как мхи отрастут, начинается новый подъем численности леммингов.

Возможны колебания численности популяции под влиянием погодных условий, паразитов и хищников.

Существует особый вариант регулирования плотности популяций, который называется «оппортунистическим», т.е. не укладывающимся в «правильные» законы, описанные экспоненциальной или логистической кривой.

У эксплерентов (r‑стратегов) происходят вспышки численности в том случае, если появляются обильные ресурсы. При этом рост численности происходит либо за счет того, что начинают развиваться особи из покоящихся диаспор (скажем, почвенного банка семян), либо за счет массового «десанта» в стадии яиц (скажем, мух, налетевших на труп животного). Так как конкуренция в силу обилия ресурсов слаба то израсходовав их изобилие, популяция погибает целиком.

У растений‑эксплерентов при повышении плотности популяции конкуренция возрастает, но самоизреживания (как у деревьев‑виолентов) не происходит, а уменьшается размер особей в десятки и сотни раз. При этом растения проходят весь жизненный цикл и способны дать семена.

Дж. Харпер (Harper, 1977) назвал такой тип регуляции плотности популяций растений‑однолетников «пластичностью» и противопоставил его самоизреживанию. Эти два типа регулирования плотности в популяциях растений связаны переходом: у большинства видов с вторичными стратегиями при повышении плотности популяции происходит одновременно и уменьшение размера особей, и самоизреживание.

На знании этих закономерностей построено обоснование нормы высева культурных растений. Вначале при увеличении нормы высева урожай растет, но потом начинает снижаться (рис. 17). Выбирается та норма высева, которая обеспечивает максимальный урожай. Впрочем, иногда ее несколько завышают, чтобы культурные растения могли подавлять популяции сорных растений. При усилении гербицидного контроля в этом нет необходимости.

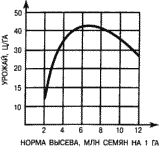
Рис. 17. Зависимость урожая пшеницы от нормы высева при оптимальных экологических условиях.

Контрольные вопросы

1. Охарактеризуйте экспоненциальную модель роста популяции.

2. Почему модель экспоненциального роста редко наблюдается в природных популяциях?

3. Из каких фаз состоит логистическая модель роста популяции?

4. Какие причины вызывают циклическую динамику популяций?

5. Какие популяции называются оппортунистическими?