Оптимизация распределения ресурсов по векторному критерию

Рассмотрим, каким образом подход к оптимизации распределения ресурсов, изложенный в разделе 3 данной лекции, может быть обобщен для нахождения 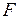-оптимальной стратегии 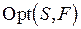, где отношение 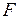формируется вектором критериев 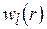, , 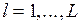(2.4).

Предположим, аддитивно-сепарабельный критерий 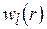формирует бинарное отношение:

(5.1) ,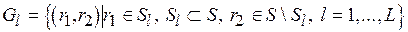

где 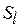– подмножество, являющееся одновременно внутренне и внешне устойчивым в модели выбора , или стратегия, условно оптимальная по критерию .

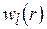Пусть

(5.2) ,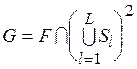

т.е. 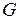– сужение 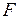на множество 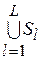(индекс 2 – степень множества).

Рассмотрим работу 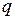, , 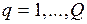состоящую из 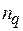задач и описываемую вектором 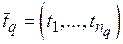, где 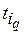, , 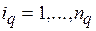представляет собой длительность выполнения 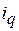-й задачи. Чтобы найти длительность работы, условно оптимальную по критерию 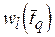, используем функциональное уравнение (3.1). Вспомогательная зависимость для поиска условно оптимальной длительности 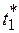при запасе 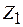времени к началу выполнения первой задачи 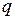-й работы имеет следующий вид:

(5.3) .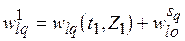

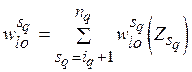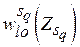В (5.3) , где – условный экстремум критерия 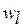при заданном значении запаса 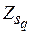по времени к моменту запуска 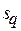-й задачи.

Условный оптимум длительности выполнения 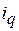-й задачи, 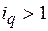, отыскивается с помощью зависимости

(5.4) .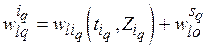

В (5.4) 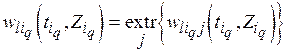, т.е. отбирается наилучшая комбинация типов базовых процессоров и коммуникационной среды.

Будем полагать, что 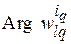, где 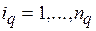, множество значений переменных функций 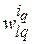(5.3), (5.4). Любой, в том числе и условно оптимальной длительности 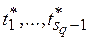, соответствует одно и только одно значение запаса 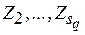по времени. Тогда 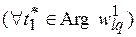существует, по крайней мере, одна последовательность 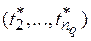такая, что 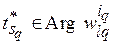и при

(5.5) ,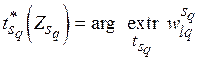

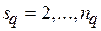
достигается условный экстремум функции 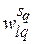для фиксированного запаса 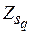(см. (3.2)).

Вектор 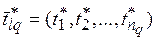представляет собой условно оптимальную по критерию 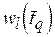длительность работы 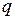. Тогда по аналогии с (3.3) условно оптимальное назначение 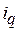-й задачи 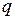-й работы определяется как

(5.6) ,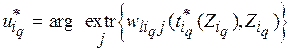

где 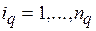, , 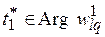а 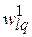строится в соответствии с (5.3).

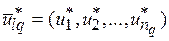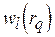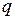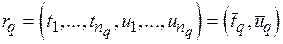Вектор – условно оптимальное по критерию назначение для работы , где . Условно оптимальная по критерию 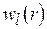стратегия распределения ресурсов для последовательности 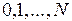критических работ представляет собой совокупность векторов 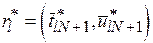, где , .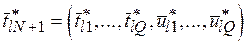

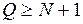Формальным обоснованием процедуры поиска оптимальной стратегии распределения вычислительных ресурсов в системах реального времени служат следующие далее утверждения.

Лемма. Пусть 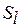в (5.1) представляют собой стратегии, условно оптимальные по аддитивно-сепарабельным критериям 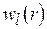, , 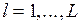и имеет место (5.2).

Если 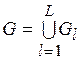, а 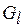в (5.1) таковы, ч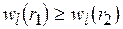то , то

(5.7) .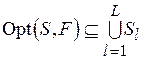

Если отношение 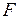антисимметрично, то в (5.7) имеет место равенство.

Доказательство леммы приводится в Приложении.

Теорема 2. Положим, что 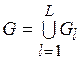, а отношение 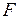антисимметрично. 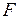-оптимальная стратегия существует тогда и только тогда, когда 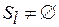для .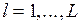

Это утверждение достаточно очевидно. Действительно, пусть 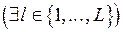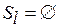. Это означает, что 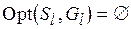и 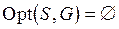. Поскольку согласно (5.2) 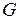– сужение 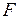, то и 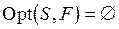. Теперь предположим, 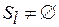, 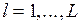. Тогда в соответствии с леммой .

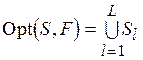Таким образом, теорема 2 устанавливает критерий существования 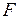-оптимальной стратегии распределения ресурсов, где 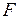антисимметрично. Такой, казалось бы, вырожденный случай, когда 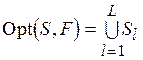, интересен с практической точки зрения.

Усиление требований к отношениям 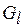чревато тем, что оптимальная стратегия будет охватывать небольшое число возможных сценариев наступления различного контрольных событий в системе, влияющих на выбор конкретного варианта распределения. Как будет показано в разделе 6 настоящей лекции, зачастую имеет смысл формировать оптимальную стратегию как объединение условно оптимальных стратегий 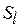, каждая из которых порождается на основе применения уравнений (5.3) - (5.6) и соответствующего критерия .

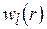Необходимое и достаточное условие существования оптимальной стратегии – формирование непустых условно оптимальных стратегий. Это означает, что должен быть найден условно оптимальный план выполнения задач для каждого из критериев эффективности. Такого плана может и не существовать в случае, например, когда нельзя разрешить возникающих коллизий из-за отсутствия свободных процессоров. Тогда необходимо соответствующим образом трансформировать модель (граф) системы задач, в частности, понизить уровень параллелизма.

Теорема 3. Предположим, распределение ресурсов осуществляется для последовательности 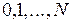критических работ на основе функциональных уравнений (5.3) - (5.6) по вектору 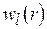, , 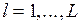аддитивно-сепарабельных критериев (2.4), формирующих отношения 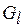(5.1). Коллизии разрешаются путем введения процессоров, тип которых совпадает с типом базового. Тогда для 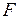-оптимальной стратегии выполняется (5.7).

Справедливость теоремы 3 непосредственно следует из леммы, поскольку подмножества 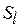, генерируемые на основе применения функциональных уравнений (5.3) - (5.6), являются внутренне и внешне устойчивыми в моделях выбора :

;

.

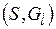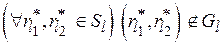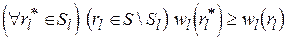
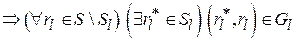Пусть 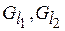– антисимметричные отношения. Поскольку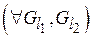 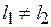, , 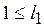, , 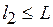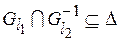где 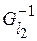– отношение, обратное 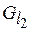, а 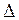– диагональное (единичное) отношение, то 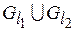– антисимметрично. Следовательно, и отношение 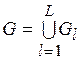тоже антисимметрично. Тогда в соответствии с леммой .

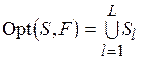Если 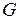– асимметричная часть отношения 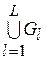, например, отношение Парето, т.е. 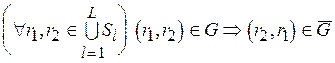, то согласно лемме .

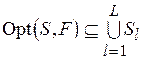По существу теорема 3 утверждает, что поиск 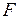-оптимальной стратегии распределения ресурсов сводится к последовательной генерации стратегий 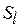, условно оптимальных по частным критериям 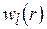, , 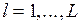и отбору альтернатив на основе их сравнения по частным отношениям 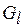(5.1). При этом применение уравнений (5.3) - (5.6) обеспечивает внутреннюю и внешнюю устойчивость генерируемых подмножеств 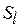альтернатив распределения ресурсов.