Значения критерия Диксона

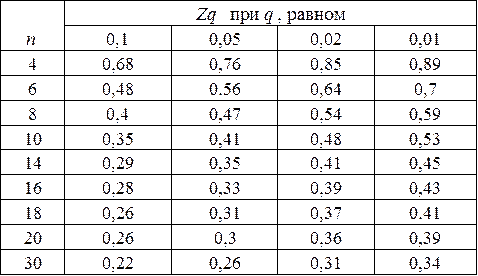
Составляется вариационный возрастающий ряд из результатов измерений: 24,9; 25,1; 25,1; 25,2; 25,2; 25,6 м. Для крайнего члена этого ряда 26,6 м расчетный критерий Диксона

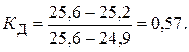
Как следует из табл. 6, по этому критерию результат 25,6 м может быть отброшен как промах при уровне значимости q=0,05.

Среднеквадратичной ошибкой среднего арифметического называется величина

.

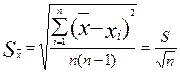Это фундаментальный закон возрастания точности при росте числа измерений. Ошибка 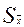характеризует точность, с которой получено среднее значение измеряемой величины 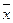. Результат записывается в виде .

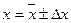Эта методика расчета ошибок дает хорошие результаты в том случае, если одна и та же величина измерялась не менее 30 раз. В 1908 году Стъюдент показал, что статистический подход справедлив и при меньшем числе измерений. Распределение Стъюдента при числе измерений 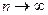переходит в распределение Гаусса, а при малом числе измерений отличается от него.

По Стъюденту для расчета абсолютной ошибки при малом числе

измерений вводится специальный коэффициент t (коэффициент Стъюдента), зависящий от надежности Р и числа измерений n:

,

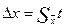где 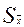среднеквадратическая ошибка среднего арифметического.

Значения коэффициентов Стъюдента приведены в таблице 1.

Таблица 1. Коэффициенты Стъюдента, t
n	Значения надежности, Р
0.6	0.8	0.95	0.99
	1.376	3.078	12.706	63.657
	1.061	1.886	4.303	9.925
	0.978	1.638	3.182	5.841
	0.941	1.533	2.776	4.604
	0.920	1.476	2.571	4.032
	0.906	1.440	2.447	3.707
	0.896	1.415	2.365	3.499
	0.889	1.397	2.306	3.355
	0.883	1.383	2.262	3.250
	0.879	1.372	2.228	3.169
…	…	…	…	…
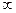
	0.842	1.282	1.960	2.576

Коэффициенты Стъюдента при Р=0.95 &

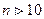
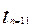= 2.201 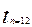= 2.1788 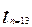= 2.1604 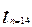=2.1448 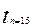=2.1314 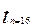=2.1190 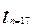=2.1098 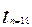=2.1009 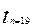=2.0930 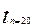=2.0860

Из рассмотренного выше следует:

• величина среднеквадратичной ошибки позволяет вычислить вероятность попадания истинного значения измеряемой величины в любой интервал вблизи среднего арифметического;

• при безграничном увеличении числа измерений 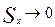, то есть интервал, в котором с заданной вероятностью находится истинное значение измеряемой величины 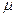, стремится к нулю с увеличением числа измерений. При этом точность увеличивается до тех пор, пока случайная ошибка не станет сравнимой с систематической. Дальнейшее увеличение числа измерений нецелесообразно, так как конечная точность результата будет зависеть только от систематической ошибки. Зная величину систематической ошибки, нетрудно задаться допустимой величиной случайной ошибки (например, в 10% от систематической). Задавая для выбранного таким образом доверительного интервала определенное значение Р (например, Р=0.95), нетрудно найти необходимое число измерений, гарантирующее малое влияние случайной ошибки на точность результата измерений.

Ошибка! Ошибка связи.

Рис. 2.

На графике нормального распределения погрешностей (рис. 2) по оси абсцисс отложены интервалы с границами 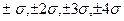и указаны соответствующие им значения Р доверительной вероятности (надежности). Как видно из рис.2, ограничение случайной погрешности интервалом 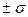соответствует доверительной вероятности всего лишь в 68%. Такая оценка не дает уверенности в высоком качестве измерений, так как 32% от всего числа измерений может выйти за пределы указанного интервала и может дезинформировать потребителя информации. В целях единообразия в оценивании случайных погрешностей интервальными оценками чаще всего доверительная вероятность принимается Р=0.95 (соответствует интервалу 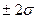). Лишь для особо точных и ответственных измерений допускается применять более высокую доверительную вероятность.

Для удобства в таблице 3 приведены значения числа измерений в зависимости от уровня задаваемой относительной ошибки и надежности результата Р.

Таблица 3.Число измерений n для получения ошибки изменения с заданной надежностью Р
	Значения Р
0.5	0.9	0.95	0.99
1.0
0.5
0.4
0.3
0.2
0.1

Если случайная величина име­ет нормальное распределение, то вероятность ее отклонения от сво­его среднего значения не более чем на σ составляет 68,27 %, не бо­лее чем на 2σ — 95,45 % и не более чем на Зσ — 99,73 %.

Поскольку величина 0,9973 близка к единице, практически считается невозможным отклонение нормального распределения случайной величины от математического ожидания более чем на Зσ. Это правило, справедливое только для нормального распределения, называется правилом трех сигм. Нарушение его имеет вероятность Р = 1 - 0,9973 = 0,0027. Этим правилом пользуются при установле­нии границ допустимых отклонений допусков геометрических ха­рактеристик изделий и конструкций.

Учитывая изложенное, можно рекомендовать следующий порядок операций при обработке результатов прямых измерений:

1. Результаты измерений оформить в таблицу;

2. Вычислить среднее значение из n измерений;

3. Найти погрешности отдельных измерений;

4. произвести проверку выборки изменений на наличие промахов;

5. Вычислить квадраты погрешности отдельных измерений;

6. Определить среднеквадратичную ошибку среднего арифметического;

7. Задаться значением надежности (например, Р=0.95);

8. Определить коэффициент Стъюдента t для заданных надежности и числе произведенных измерений;

9. Найти доверительный интервал (погрешность измерения);

10. Если величина погрешности результата измерения 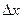окажется сравнимой с величиной погрешности прибора 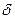, то в качестве границы доверительного интервала принять:

.

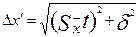Если одна из ошибок меньше другой в три раза и более, то ее необходимо отбросить. ---------------------------------------------------------

На практике при прямых измерениях всегда производят 2 – 3 измерения, по которым убеждаются в воспроизводимости результатов, соблюдении методики измерений. Если разброс показаний превышает приборную погрешность, то производится 5 – 6 измерений и находится случайная погрешность .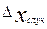

Чтобы получать более полное представление об измерениях некоторой величины и иметь возможность сравнивать точность различных измерений (в том числе и величин разной размерности), принято находить и приводить относительную ошибку результата.

Окончательная запись результатов измерений величины х с учетом ошибок измерений должна иметь вид:

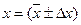, с указанием размерности;

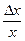, в процентах.

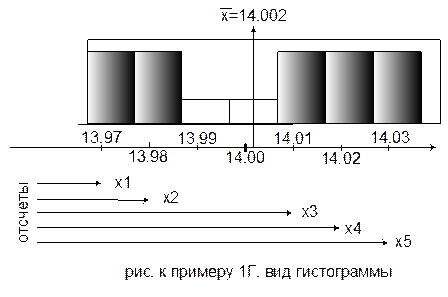
Пример 1. Последовательно микрометром произведено 5 измерений диаметра стержня. Систематическая ошибка измерения равна 0.005 мм. Результаты измерений и данные вычислений сведены в таблицу 2.

Измерение диаметра стержня Таблица 2

n	d, мм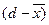
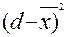
	14.03	0.028	0.000784
	14.01	0.008	0.000064
	13.97	-0.032	0.001024
	13.98	-0.022	0.000484
	14.02	0.018	0.000324
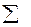
	70.01		0.00268

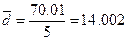мм

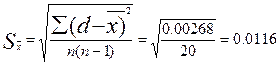
Задавшись значением надежности Р=0.95 по таблице находят соответствующее значение коэффициента Стъюдента t=2.776

Вычисляют абсолютную ошибку:

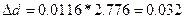
	проверка	вычислений	в среде	exel
	14,03	0,03	0,000784
	14,01	0,01	6,4E-05
	13,97	-0,03	0,001024
	13,98	-0,02	0,000484
	14,02	0,02	0,000324
сумма	70,01		0,00268	0,032135
				2,776	t
среднее	14,002		0,000134	0,011576

14,002 ± 0.032(135)

Вычисленная абсолютная ошибка примерно в 6 раз больше заданной систематической ошибки, поэтому последней можно пренебречь.

Окончательный результат измерений:

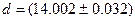при Р=0.95

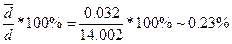
Обработку результатов измерений удобно производить, используя возможности математически ориентированной вычислительной системы MathCAD.

Для конструирования блоков в среде Mathcad используются три встроенных в систему редактора: текстовый, формульный и графический. Текстовый редактор служит для создания различных текстовых комментариев. Для вставки текста требуется выйти в меню «вставка» и в нем выбрать «текстовая область». Формульный редактор служит для создания математических выражений. Редактирование формул производится аналогично редактированию текстовых документов. Графический редактор служит для вывода информации в виде различных графиков и их редактирования.

Для вычисления погрешностей измерения в MathCAD используются следующие встроенные функции:

• для вычисления среднего арифметического применяют функцию 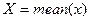, где 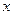- вектор, содержащий 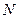значений измеренной физической величины;

• для вычисления средней квадратичной ошибки отдельного результата используется функция ;

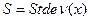• для определения погрешности вычисления среднего используют выражение ;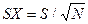

• длина массива определяется через функцию ;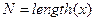

• интервал 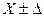, в который с заданной достоверностью Р попадает истинное значение измеряемой величины, определяется с помощью выражения 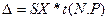, где t – коэффициент Стъюдента, выбираемый из таблиц в соответствии с выбранными значениями достоверности Р.

Пример 2. Пусть произведены измерения длины отрезка l = (15.4± 0.3) мм и длины волны 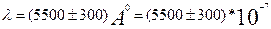мм. Абсолютная ошибка второго измерения 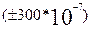мм меньше, чем первого 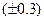мм, но сравнивать точности измерения можно лишь сравнив относительные ошибки измерений:

.

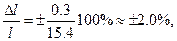
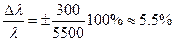Отсюда видно, что точность измерения длины волны ниже, чем измерение длины отрезка.

Важными характеристиками результатов измерения являются варианты графической иллюстрации рассеяния в виде построения гистограммы и (или) полигона распределения, наглядно показывающие частоту (или частость), с которой в пределах выбранного диапазона встречается тот или иной отсчет. Для их построения необходимо:

1) ранжировать имеющийся массив данных (расположить их по возрастанию);

2) выбрать число интервалов разбиения диапазона (правило Старджеса:

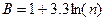, где n – число измерений, В – число интервалов, округляется до целого в меньшую сторону;

3) определить ширину интервала: ;

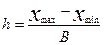4) графически: по оси абсцисс отложить границы интервалов разбиения, а по оси ординат от середин интервалов отложить частоты (частость) попадания в них отсчетов 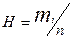, где 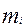- количество измерений, попавших в данный интервал.

Полигон строится путем соединения отрезками прямой ординат, соответствующих частотам попадания отсчета в интервал, а гистограмма представляет собой ступенчатую фигуру из прямоугольников, основаниями которых являются сами интервалы, а высоты равны частотам попадания отсчетов в них.

Средства измерения

2.1. Гладкие калибры (средства контроля).

Назначение, область применения

В современном массовом и крупносерийном производстве для контроля годности размеров обрабатываемых деталей используют особые средства измерений – калибры.

Калибр – это бесшкальный контрольно-поверочный инструмент, предназначенный для контроля правильности размеров или формы и расположения поверхностей изделия или его частей.

В зависимости от способа оценки годности размера, калибры делятся на нормальные и предельные.

Нормальные калибры используются для проверки степени соответствия действительного размера детали ее номинальному размеру. В качестве нормальных калибров широко используются различные шаблоны для проверки радиусов скругления, различных углов, профилей сложных фасонных поверхностей и т. д.

Большое распространение в настоящее время получили предельные калибры, исключающие субъективность результата контроля. Предельным калибром нельзя установить числовое значение действительного размера, можно только установить, находится ли размер детали в пределах заданного допуска, т. е. является ли размер «годным» или нет.

Ошибка! Ошибка связи.

Рис. 3. Калибры гладкие

Калибры изготавливают по одной из следующих схем:

• однопредельными, содержащими только один проходной или непроходной калибры;

• двухсторонними двухпредельными (наиболее распространены), у которых проходной и непроходной калибры расположены с разных сторон;

• односторонними двухпредельными, у которых проходной и непроходной калибры расположены с одной стороны последовательно один за другим.

Универсальные СИ.