Обработка результатов измерения
Технические измерения. Погрешности измерений
По своим свойствам погрешности делятся на систематические и случайные. Систематическая погрешность при использовании одних и тех же СИ и метода измерений остается постоянной или изменяется по определенному известному закону. Поэтому она может быть устранена (учтена) путем введения поправки. Систематическая погрешность зависит только от методики эксперимента, конструкции и технического состояния измерительных приборов при достаточно высоком профессиональном уровне экспериментатора. Систематическую ошибку нельзя устранить при повторном измерении.
Если при повторных измерениях одной и той же величины одними и теми же СИ и по неизменной методике получают различные результаты, которые носят случайный характер, то рассеяние показаний обусловлено случайной погрешностью измерений. В случайные погрешности не включаются так называемые промахи - грубые погрешности, которые возникают вследствие различных причин, например, неправильных действий экспериментатора, резких скачков напряжения в электросети и т. д.
Обработка результатов измерения
Истинное значение измеряемой величины x при любых измерениях остается неизвестным, а в результате измерений получают его оценку 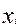 .
.
Разность величин 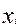 и x называется погрешностью измерений
и x называется погрешностью измерений

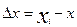 ,
, 
которую нельзя определить, так как истинная величина неизвестна. Поэтому погрешность измерений приходится оценивать с использованием косвенных данных.
Систематическая погрешность зависит от методики эксперимента, технического состояния приборов, профессионального уровня оператора. Сведения о приборной систематической погрешности представлены в паспорте прибора.
Для уменьшения влияния отдельных случайных ошибок на результат необходимо производить измерения несколько раз. Ряд значений результатов измерений (РИ) некоторой величины х: х1,х2,..., х n получил название выборки. Имея такую выборку, можно, так или иначе, дать оценку результата измерений и обозначить ее 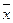 . Так как это значение не является истинным, то необходимо оценить его ошибку (погрешность). Обозначая оценку ошибки измерения как
. Так как это значение не является истинным, то необходимо оценить его ошибку (погрешность). Обозначая оценку ошибки измерения как 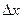 , можно результат записать в виде
, можно результат записать в виде
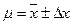 .
.
Эта оценка не является точной, так как неточны оценка результата 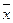 и ее погрешность
и ее погрешность 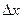 , поэтому запись результата измерений должна сопровождаться указанием его надежности Р. Под надежностью или доверительной вероятностью понимают вероятность того, что истинное значение измеряемой величины заключено в интервале, указанном записью результата измерения. Сам этот интервал называется доверительным интервалом.
, поэтому запись результата измерений должна сопровождаться указанием его надежности Р. Под надежностью или доверительной вероятностью понимают вероятность того, что истинное значение измеряемой величины заключено в интервале, указанном записью результата измерения. Сам этот интервал называется доверительным интервалом.
Например, измеряя длину некоторого отрезка, окончательный результат записан в виде
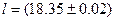 мм,
мм, 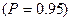 .
.
Это означает, что из 100 шансов – 95 за то, что истинное значение длины отрезка заключается в интервале от 18.33 до 18.37 мм.
Таким образом, задача обработки результатов измерений заключается в том, чтобы имея выборку результатов измерений найти:
• оценку результата измерений 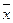 ;
;
• его ошибку 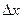 ;
;
• надежность Р.
Эта задача решается с помощью элементов теории вероятности и математической статистики.
На практике в большинстве случаев случайные ошибки подчиняются нормальному закону распределения (закон Гаусса):
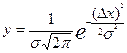 ,
,
где 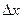 - отклонение величины от истинного значения,
- отклонение величины от истинного значения,
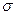 - среднеквадратическая ошибка,
- среднеквадратическая ошибка,
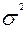 - дисперсия, характеризующая разброс случайных величин.
- дисперсия, характеризующая разброс случайных величин.
Площадь фигуры, заключенной между кривой Гаусса (рис. 1), осью ОХ и двумя ординатами из точек 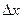 1 и
1 и 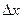 2 (заштрихованная область на рисунке), численно равна вероятности, с которой любой отсчет попадет в интервал <
2 (заштрихованная область на рисунке), численно равна вероятности, с которой любой отсчет попадет в интервал < 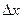 1 ,
1 , 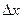 2 >.
2 >.
Ошибка! Ошибка связи.
Рис. 1. Распределение Гаусса
Поскольку кривая симметрична относительно оси ОY, можно утверждать, что равные по величине, но противоположные по знаку ошибки равновероятны, что дает возможность в качестве оценки результатов измерений брать среднее значение элементов выборки:
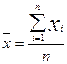 ,
,
где n – число измерений.
Если в одних и тех же условиях проделано n измерений, то наиболее вероятным значением измеряемой величины будет ее среднее арифметическое. Величина 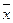 стремится к истинному значению
стремится к истинному значению 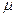 измеряемой величины при
измеряемой величины при 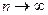 .
.
Средней квадратичной ошибкой отдельного результата измерения называется величина
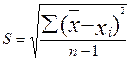 .
.
Средняя квадратичная ошибка характеризует ошибки отдельных измерений. При 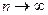 величина S стремится к пределу
величина S стремится к пределу 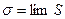 . С увеличением
. С увеличением 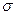 увеличивается разброс отсчетов, то есть снижается точность измерений.
увеличивается разброс отсчетов, то есть снижается точность измерений.
Промахи (грубые погрешности измерений) могут сильно исказить результат измерений, поэтому их исключение из ряда измерений обязательно. Существует несколько критериев для оценки промахов [9]. При числе измерений n < 20 целесообразно применять критерий Романовского. При этом вычисляют отношение
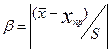 (3)
(3)
где хпр − проверяемый результат измерения (результат, вызывающий сомнение).
Полученное значение β сравнивают с теоретическим значением βт (табл. 1), определенным для установленного уровня значимости q (q = 1 − P).
Таблица 1. Значения βт = f (n, q) [9]
| Уровень значимости q | Число измерений n | |||||||
| 0,01 | 1,73 | 2,16 | 2,43 | 2,62 | 2,75 | 2,90 | 3,08 | |
| 0,02 | 1,72 | 2,13 | 2,37 | 2,54 | 2,66 | 2,80 | 2,96 | |
| 0,05 | 1,71 | 2,10 | 2,27 | 2,41 | 2,52 | 2,69 | 2,78 | |
| 0,10 | 1,69 | 2,00 | 2,17 | 2,29 | 2,39 | 2,49 | 2,62 |
Если число измерений невелико (n ≤ 10), можно использовать критерий Шовине [9]. В этом случае считают, что результат хi=х прявляется промахом, если |х− хпр|превышает значения, приведенные ниже [9]:
 |
| 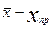 |> {1.6 S при п=3
|> {1.6 S при п=3
1.7 S при п=6
1.9 S при п=8
2.0 S при п=10 }
Пример 1. При измерении диаметра вала микрометром были получены значения: 12,24; 12,26; 12,28; 12,28; 12,31; 12,34; 12,40; 12,41; 12,42; 12,42; 12,45; 12,80 мм. Число измерений n= 12. Последний результат (12,80 мм) вызывает сомнения. Принимаем Р= 0,95, тогда q= 0,05.
Выполнив расчеты, получили значения − 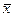 = 12,38 мм; S= 0,15 мм. Так как n< 20 для определения промахов используем критерий Романовского, определив его по формуле (3):
= 12,38 мм; S= 0,15 мм. Так как n< 20 для определения промахов используем критерий Романовского, определив его по формуле (3): 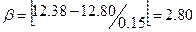
Для n=12 и q= 0,05 βт =2,52 (см. табл. 1). Т.е. β > βт и результат хi = хпр = 12,80 мм необходимо «отбросить», как промах.
После исключения результатов, содержащих промахи, определяют новые значения хи Sи, если есть сомнения, процедуру проверки наличия промахов повторяют.
Пример 2. При измерении диаметра вала микрометром были получены значения: 30,12; 30,27; 30,28; 30,29; 30,32; 30,38 мм. Число измерений n= 6. Первый результат (30,12 мм) вызывает сомнения.
Выполнив расчеты, получили значения х= 30,28 мм; S=0,086 мм. Так как n< 10, для определения промахов используем критерий Шовине:
|30,28−30,12|=| 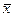 -хпр|= 0,16 мм,
-хпр|= 0,16 мм,
что больше, чем 1,7 S= 0,146 мм. Следовательно, причиной появления результата хi = хпр = 30,12 мм является промах и этот результат необходимо исключить из полученного ряда результатов измерений.
Критерий Шовине
Критерий применяют при числе измерений менее 20. сначала определяют значение 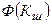 по зависимости
по зависимости
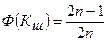 ,
,
а затем 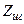 , значение которого приводится в табл.
, значение которого приводится в табл.
Таблица
Значения критерия Шовине
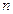
| ||||||||
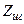
| 1,38 | 1,53 | 1,65 | 1,73 | 1,80 | 1,86 | 1,92 | 1,96 |
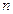
| ||||||||
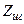
| 2,03 | 2,10 | 2,15 | 2,20 | 2,24 | 2,32 | 2,39 | 2,57 |
Если разность между сомнительным результатом 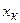 и средним арифметическим значением
и средним арифметическим значением 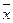 (остаточная погрешность) превосходит по модулю величину
(остаточная погрешность) превосходит по модулю величину 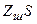 , то результат отбрасывается как промах.
, то результат отбрасывается как промах.
Дата добавления: 2020-10-01; просмотров: 590;











