Функции для работы с векторами и матрицами
Для работы с векторами и матрицами имеется множество функций, входящих в пакет linalg.
Операции со структурой отдельного вектора 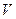 и матрицы
и матрицы 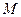 :
:
§ coldim(M) – возвращает число столбцов матрицы 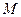 ;
;
§ rowdim(M) – возвращает число строк матрицы 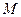 ;
;
§ vecdim(V) – возвращает размерность вектора 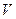 ;
;
§ col(M,i) – возвращает 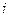 -й столбец матрицы
-й столбец матрицы 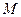 ;
;
§ row(M,,j) – возвращает 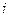 -ю строку матрицы
-ю строку матрицы 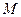 ;
;
§ minor(M,i,j) – возвращает минор матрицы 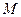 для элемента с индексами
для элемента с индексами 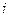 и
и 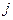 ;
;
§ delcols(M,i..j) – удоляет столбцы матрицы 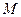 от
от 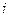 -го до
-го до 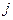 -го;
-го;
§ delrows(V,i..j) – удоляет строки матрицы 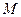 от
от 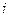 -й до
-й до 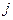 -й;
-й;
§ extend(M,m,n,x) – расширяет матрицу 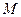 на
на 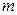 строк и
строк и 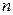 столбцов с применением заполнителя
столбцов с применением заполнителя 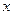 .
.
Основные векторные и матричные операции:
§ dotprod(U,V) – возвращает скалярное произведение векторов 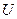 и
и 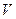 ;
;
§ crossprod(U,V) – возвращает векторное произведение векторов 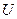 и
и 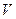 ;
;
§ norm(V) или norm(M) – возвращает норму вектора и матрицы;
§ copyinto(A,B,i,j) – копирует матрицу 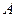 в
в 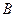 для элементов последовательно от
для элементов последовательно от 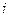 до
до 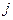 ;
;
§ concat(M1,M2) – возвращает объединённую матрицу с горизонтальным слиянием матриц 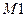 и
и 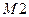 ;
;
§ stack(M1,M2) – возвращает объединённую матрицу с вертикальным слиянием матриц 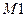 и
и 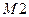 ;
;
§ matadd(A,B) и evalm(A+B) – возвращает сумму матриц 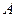 и
и 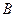
§ multiply(A,B) и evalm(A*B) – возвращает произведение матриц 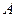 и
и 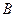
§ adjoint(M) или adj(M) – возвращает присоединённую матрицу, такую что даёт диагональную матрицу, определитель которой есть 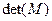
§ charpoly(M,lambda) – возвращает характеристический полином матрицы 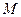 относительно заданной переменной lambda;
относительно заданной переменной lambda;
§ det(M) – возвращает детерминант (определитель) матрицы 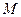 ;
;
§ Eigenvals(M,vector) – инертная форма функции, возвращающей собственные значения матрицы 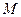 и (при указании необязательного параметра vector) соответствующие им собственные векторы)
и (при указании необязательного параметра vector) соответствующие им собственные векторы)
§ jordan(M) – возвращает матрицу 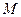 в форме Жордана;
в форме Жордана;
§ transpose(M) – возвращает транспонированную матрицу 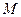 ;
;
§ inverse(M) или evalm(1/M) – возвращает матрицу, обратную к 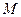 ;
;
§ singularvals(A) – возвращает сингулярные значения массива или матрицы 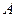 .
.
Дата добавления: 2020-10-01; просмотров: 410;











