РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОЙ АЛГЕБРЫ
Рассмотрим основные определения относящиеся к линейной алгебре.
Матрица ( 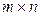 ) – прямоугольная двумерная таблица, содержащая
) – прямоугольная двумерная таблица, содержащая 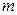 строк и
строк и 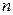 столбцов элементов, каждый из которых может быть представлен числом, константой, переменной, символьным или математическим выражением.
столбцов элементов, каждый из которых может быть представлен числом, константой, переменной, символьным или математическим выражением.
Квадратная матрица – матрица, у которой число строк равно числу столбцов.
Сингулярная (вырожденная) матрица – квадратная матрица, у которой детерминант (определитель) равен нулю. Линейные уравнения с почти сингулярными матрицами могут давать большие погрешности при решении.
Транспонированная матрица – матрица, у которой столбцы и строки меняются местами, т.е. элементы транспонированной матриц удовлетворяют условию 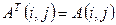 .
.
Обратная матрица – это матрица 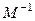 , которая, будучи умноженной на исходную матрицу
, которая, будучи умноженной на исходную матрицу 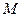 , даёт единичную матрицу
, даёт единичную матрицу 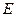 .
.
Ранг матрицы – наибольший из порядков отличных от нуля квадратной матрицы.
Определитель матрицы – это многочлен от элементов квадратной матрицы, каждый элемент которого является произведением 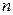 элементов, взятых по одному из каждых строк и каждого столбца со знаком произведения, заданным четностью перестановок:
элементов, взятых по одному из каждых строк и каждого столбца со знаком произведения, заданным четностью перестановок: 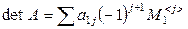 , где
, где 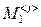 – определитель матрицы
– определитель матрицы 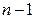 , полученной из матрицы
, полученной из матрицы 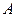 вычёркиванием первой строки и
вычёркиванием первой строки и 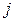 -го столбца. В таком виде определитель легко получить в символьных вычислениях.
-го столбца. В таком виде определитель легко получить в символьных вычислениях.
Идемпотентная матрица – матрица, отвечающая условию 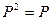 .
.
Симметричная матрица – матрица отвечающая условию 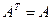 .
.
Ортогональная матрица – матрица, отвечающая условию 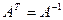 .
.
Собственные значения матрицы – корни её характеристического многочлена.
Норма – обобщенное понятие абсолютной величины числа.
Норма трёхмерного вектора 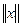 – его длина.
– его длина.
Норма матрицы – значение 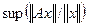 .
.
Дата добавления: 2020-10-01; просмотров: 429;











