АЛЕКСАНДРИЙСКИЙ ПЕРИОД РАЗВИТИЯ НАУКИ

Третий этап развития античной науки после ионийского и афинского – эллинский, начался после завоевания Александром Македонским греческих городов – полисов (330 г. до н.э.). Научным центром становится новая столица Египта Александрия, основанная Александром в 332 г. до н.э. За расширением границ империи последовало оживление торговли, ремёсел, транспорта и военного дела. А.Македонский и его преемники – династия Птолемеев предприняли первую попытку государственной организации и финансирования науки. В Александрии в III в. до н.э. был организован Мусейон (греч. «храм муз»), явившийся первым научно-исследовательским институтом, библиотекой и музеем, где сосредоточились уникальные памятники древнейшей науки.

В основу Александрийской библиотеки была положена библиотека Аристотеля. Считалось, что в мире нет какого-либо более или менее ценного произведения (оригинала или копии), которое не хранилось бы в Александрийской библиотеке. По разным данным в период расцвета она насчитывала от пятисот до семисот тысяч книг. Сотни грамотных рабов ежедневно трудились над их переписыванием и сортировкой. Как научная школа Мусейон стал преемником Ликея и на первых порах был тесно с ним связан. Последний выдающийся руководитель Ликея – Стратон преподавал одновременно в Афинах и в Александрии. Наибольший вклад эллинская наука внесла в математику, механику (в смысле создания простых механизмов), оптику, гидравлику и астрономию. ВIII в. до н.э. наряду с папирусом начинает использоваться пергамент (названный по имени малоазиатского полиса Пергама) – выделанная особым образом кожа телят. Листы пергамента свивались в свитки. Отдельный свиток назывался «томос» (отрезанная часть). На пергаменте можно было писать с двух сторон и использовать его повторно. С александрийским этапом античной науки связаны имена Евклида, Архимеда, Эратосфена, Птолемея, Герона, Гиппарха, Аристарха Самосского и многих других известных учёных.

2. РОЖДЕНИЕ ПНЕВМАТИКИ (ФИЛОН, КТЕСИБИЙ, ГЕРОН)

В интеллектуальном климате Афин и Александрии были существенные различия. Учёные Мусейона не занимались созданием всеобщих теорий, как это делали греческие философы классического периода. Они сосредоточились на изучении отдельных явлений и смогли добиться в этом реальных успехов. Как отмечает Флорис Коэн: «афиняне мыслили о всеобщем, а александрийцы о частном» .[1]Например, Стратон продолжил исследование свободного падения и, в ходе наблюдения, заметил, что капли удаляются друг от друга по мере приближения к Земле, а тело, падающее с большей высоты, при падении бьётся о землю сильнее, то есть имеет большую скорость.

Другое важное отличие учёных эллинского периода от учёных классицизма было в том, что они с меньшим снобизмом относились к знаниям, используемым в прикладных целях (изобретениям). Не случайно в эту эпоху появились работы Ктесибия (284-221 до н.э.), исследовавшего свойства газов и жидкостей. Ктесибий изобрёл гидравлические насосы и водяные часы, точно измерявшие время, за счёт поддержания постоянного уровня жидкости в сосуде, из которого вытекала вода. Важно и то, что технические изобретения века эллинизма были созданы теми же учёными, которые занимались систематическими научными исследованиями, служившими почвой для изобретений. Достаточно привести пример Архимеда или Филона (280 - 220 до н.э.), который работал в Александрии примерно в 250 г. до н.э. Филон был военным инженером, написавшим сочинение «Механика», посвящённому устройству гаваней для судов, осадных приспособлений, катапульт. В работе «Пневматика» он приводит экспериментальные доводы, подтверждавшие взгляд Анаксимена, Аристотеля и Стратона на то, что воздух является реальной субстанцией. Например, если погрузить амфору в воду открытым горлышком вниз, вода не станет её наполнять, поскольку её не пустит воздух. Но если позволить воздуху выйти, открыв отверстие в донышке, то вода заполнит сосуд.

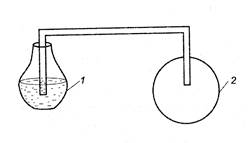В книге «Механика» Филона можно найти описание первого термоскопа. Он состоит из двух связанных трубкой сфер: одна из них пустая (2), а друга частично заполнена водой (1). Если пустой шар поместить на солнце, то можно увидеть, как в другом шаре появляются пузырьки воздуха в воде, так как «часть воздуха, - по словам Филона, - выходит наружу». Если затем поместить шар в тень, то вода поднимется в трубке, пока не попадёт в пустой шар. «Если после этого шар, куда вошёл воздух, разогреть над огнём, явление повторится. Тоже получится, если облить шар горячей водой» [2]. Таким образом, Филон пришёл к пониманию теплового расширения воздуха и активно его использовал в своих конструкциях. В трактате Филона описано множество занимательных игрушек, предназначенных для развлечения гостей во время празднеств: фонтаны с пьющими животными и поющими птицами, автоматическое устройство для раздачи святой воды в храме. Во многих из этих механизмов умело используется атмосферное давление, давление водяного пара и принцип сифона.До выяснения причин этих явлений остаётся почти две тысячи лет.

Славу Ктесибия и Филона постепенно затмил Герон Александрийский. Герон, занимался изготовлением водяных часов, но прославился, главным образом, пневматическими машинами. К таким машинам относится геронов фонтан, устройство для открывания дверей храма и эолипил, который приводился в движение паром. Автоматический театр был первым программируемым устройством.Движения механизмов происходили в строгой последовательности за счёт энергии падающих тел и гидравлики. Эолипил с полным правом можно считать прообразом паровой машины и реактивного двигателя. «Механика» Герона – это своеобразная энциклопедия античной техники. В нём он использовал и творчески развивал достижения Стратона, Евклида и Архимеда. В «Механике» рассматриваются всевозможные простые механизмы, зубчатые передачи и более сложные механизмы, сконструированные или усовершенствованные автором. Труд Герона свидетельствует о техническом уровне, достигнутом греками в эллинистический период. Они владели и техническими знаниями, и научным пониманием, достаточными, чтобы создать индустриальные машины и предвосхитить открытия ХVIII века. Но практическое применение их устройства нашли лишь в военном деле. Знания в области пневматики, привели к тому, что александрийские механики заняли промежуточную позицию между сторонниками и противниками пустоты. Онисчитали, что сплошная пустота невозможна, возможна лишь пустота в рассеянном виде, то есть между частицами материи. Она позволяет объяснить переменную плотность тел, сжимаемость и упругость воздуха. О трудах Ктесибия, Филона и Герона мы узнаём, в большей степени, из сочинений других авторов, в частности римского инженера Витрувия (I в.), так как большинство оригиналов сочинений были уничтожены во время пожара Александрийской библиотеки. Опыты Ктестбия и Герона свидетельствуют о высоком уровне развития эксперимента, ограниченного лишь уровнем развития техники и технологии.

3. РАЗРАБОТКА МАТЕМАТИЧЕСКИХ МЕТОДОВ ДЛЯ ОПИСАНИЯ МИРА (ЕВКЛИД)

Основателем математической школы в Александрии считается Евклид (III в. до н.э.). Термин «математа» (греч.,μαθήματα) восходящий к Пифагору, означает «то, что можно познать». В классической Греции (V - III в. до н.э.) математика была неразрывно связана с философией. Евклид придал ей другой смысл, обобщив идеи великих математиков – пифагорейцев, таких как Архит, Евдокс, Теэтет, он дополнил своими собственными размышлениями и объединил в логической последовательности под названием «Начала». Некоторые биографические данные о Евклиде сохранились на страницах арабской рукописи XII века: «Евклид, сын Наукрата, известный под именем «Геометра», по своему происхождению – грек, по месту жительства – сириец, родом из Тира». Евклид показал, что все известные теоремы и отношения вытекают из небольшого числа определений, аксиом и постулатов. Его метод дедукции стал образцом для учёных самых разных направлений на долгие сотни лет. Евклид брал за основу чистые аксиомы и, используя правила логической аргументации, строил доказательства теорем. Авторы других важнейших работ в области геометрии, астрономии и арифметики: К.Птолемей («Великое математическое построение»), Диафант («Арифметика»), Папп Александрийский («Математическое собрание») использовали его дедуктивный метод. А такие произведения как «Начала философии» Р.Декарта и «Математические начала натуральной философии» И.Ньютона унаследовали саму структуру труда Евклида, хотя наряду с дедукций в них используется более продуктивная для естественных наук индукция. «Начала» состоят из 13 коротких книг. В них рассматривается геометрия на плоскости и в пространстве.«Начала» многократно переписывались, переводились на другие языки, к ним писались комментарии. Эта книга отодвинула в тень все другие книги по элементарной геометрии. Евклидово трёхмерное пространство является ареной физических явлений классической физики, основы которой заложены Г.Галилеем и И.Ньютоном. Математические методы Евклид применил к решению задач геометрической оптики. Термин «оптика» происходит от греческого «опсис» (зрение) и в античную эпоху означал собственно науку о зрении. Кроме того, существовала катоптрика - наука об отражении лучей света от зеркальных поверхностей и диоптрика - наука об оптических измерениях. В «Оптике» Евклид ввёл понятие луча (хотя и идущего из глаза, согласно Платону), установил закон прямолинейного распространения света, закон отражения света, описал изображение в камере - обскуре. В «Катоптрике» он рассмотрел явления, связанные с отражением от плоских зеркал и получил изображения в них.Позднее (около 60 г.) Герон Александрийский в своём труде «Катоптрика» привёл математическое доказательство равенства углов падения и отражения, основываясь на предположении, что путь светового луча от объекта к зеркалу, а затем к глазу наблюдателя есть кратчайший возможный путь. В качестве обоснования того, почему эта закономерность наблюдается, Герон ограничился высказыванием: «Природа ничего не делает зря и не напрягает свои силы без нужды». В этом же трактате он применил закон отражения для построения хода лучей в цилиндрических (сферических) зеркалах. «Оптика» Евклида – это и первое исследование геометрии перспективы – способности человеческого глаза преобразовывать трёхмерное изображение в двумерное.Эти исследования легли в основу переворота в живописи в эпоху Возрождения.

У последователей Евклида учился Аполлоний Пергский (262 - 190 до н.э.). Его главный труд «Конические сечения» содержит 487 теорем. Описанные им кривые, полученные при пересечении плоскости с двойным конусом, широко применялись впоследствии в механике и астрономии. Особого внимания заслуживает упоминание о фокусах, которые были использованы в XVII веке И.Кеплером при построении теории орбит планет Солнечной системы.

4. АРХИМЕД – ОСНОВАТЕЛЬ ФИЗИЧЕСКОЙ НАУКИ

С Александрийским Мусейоном связано и имя Архимеда (287 - 212г. до н.э.), труды которого также ясно показывают различие между философией афинской школы и систематическими научными исследованиями конкретных явлений природы, предпринятыми александрийскими естествоиспытателями.Архимед был одним из крупнейших ученых античности. Он родился в Сиракузах в семье известного астронома Фидия. Длительное время учился в Александрии и на всю дальнейшую жизнь сохранил научные связи с учёными музея. Его принято считать математиком, хотя в ту эпоху не существовало современного разделения научного знания на отдельные отрасли. Используя математику, он нашёл законы, лежащие в основе работы многих простых механизмов.Ему удалось применил метод исчерпывания Евдокса к расчёту объёма любой фигуры, что явилось предтечей дифференциального и интегрального исчисления (идеи изложены в трактате «Псаммит» (греч, «Исчисление песчинок»)).

«Имея Евклида как образец, Архимед сделал первую попытку изложить вопросы механики, основываясь на определениях, аксиомах и постулатах»[3]. В трактате «О равновесии плоских фигур» им введено понятие центра тяжести треугольника и установлено условие равновесия рычага. Этот трактат являет образец первого исследования по математической физике. Архимед указывает, что во многих случаях центр тяжести можно определить теоретически. Затем он предлагает проверить это утверждение экспериментально, подперев тело в центре тяжести. Если эта точка найдена правильно, тело должно сохранять равновесие. Гениальным изобретением Архимеда является винт, о котором Г.Галилей писал: «Это изобретение просто чудесно, поскольку мы видим, что вода поднимается в винте, беспрерывно опускаясь». Исследуя спираль математически, Архимед дал способ построения касательной к ней. Достоверно известно, что, используя возможности сцепления бесконечного винта с шестернёй и полиспасты, Архимед смог передвинуть огромный корабль. Согласно легенде удачно поставленный эксперимент вдохновил Архимеда метафорическое высказывание: «Дайте мне точку опоры, и я сдвину Землю». По свидетельству современников Архимед построил механическую модель движения Земли, Солнца, Луны и пяти планет и описал свою конструкцию в книге «Об изготовлении небесной сферы». Этот механизм точно показывал лунные фазы и моменты наступления затмений. Возможно, удивительная находка, поднятая со дна моря в районе греческого острова Антикитер спустя два тысячелетия, является механизмом, созданным Архимедом и захваченным Марцеллом в качестве трофея во время Пунической войны[4]. Предложенная Архимедом система мира, впервые заставляла планеты двигаться вокруг Солнца, хотя само Солнце всё же двигалось вокруг Земли.

По легенде, в ходе обороны Сиракуз, Архимед поставил эксперимент, приведший к гибели римской флотилии стоявшей в бухте. Рассчитав местоположения воинов со щитами, вдоль параболоида, он сумел сфокусировать солнечные лучи и поджечь корабли, попавшие в его фокус. Сам себя к физикам Архимед никогда не причислял, но первый физический закон был установлен именно им. Легенда говорит о том, что открытие закона связано с задачей, поставленной перед ним правителем Гиероном – проверить содержание золота в жертвенном венце. Каким способом учёный это сделал неизвестно. По мнению Г.Галилея Архимед применил метод, основанный на двух открытых им законах, называемый методом двойного взвешивания[5]. Учёному нужно было доказать, что жертвенный венец изготовлен из сплава, а для этого потребовалось ввести понятие «удельный вес» (плотность вещества), соотнося вес тела с весом воды того же объёма, и определить его экспериментально для золота, серебра и сплава. Новое понятие было необходимо в дальнейшем для понимания поведения плавающих тел. Излишне говорить, насколько закон гидростатики открытый Архимедом был важен для судостроения. В Архимеде гениально сочетались качества учёного и инженера. Он намного опередил своё время. Мыслители такого уровня появились только во времена Возрождения, а если говорить о физико-математических науках, то преемников Архимеда можно найти только в XVII веке.

5. ИЗМЕРЕНИЕ РАЗМЕРОВ ЗЕМЛИ И КАРТОГРАФИРОВАНИЕ ЕЁ ПОВЕРХНОСТИ (ЭРАТОСФЕН)

Долгое время Александрийский Мусейон возглавлял Эратосфен Киренский (276 – 194 г. до н.э.). Эратосфен был разносторонним учёным: математиком, философом, географом, вёл переписку с Архимедом. Его трёхтомник «Географика» представлял собой первую попытку картографирования мира с использованием параллелей и меридианов. В 212 году до н.э. Эратосфен придумал и реализовал интересный эксперимент, который помог ему определить размеры Земли[6]. Он сравнил направление вертикали, проведённой к данному участку поверхности земного шара, с направлением параллельного пучка солнечных лучей (так как предполагалось, что Солнце располагалось на значительно большем расстоянии, чем, например, Луна) в двух пунктах, отстоящих друг от друга на известном расстоянии. Надёжных часов в то время не было, и Эратосфен обеспечивал одновременность наблюдений, выбирая полдень (когда Солнце кульминирует, то есть, находится в самом высоком положении одного и того же дня) в пунктах, расположенных на одной и той же географической долготе. Он проводил наблюдения в Александрии, где работал и сравнивал их с наблюдениями, проводившимися ранее в Сиене (современный Асуан), расположенной на расстоянии около 5 тысяч египетских стадий (около 840 км). Расстояния между населенными пунктами Египта были известны достаточно точно, так как измерялись царскими землемерами - гарпеданаптами (держателями верёвок). В Сиене в полдень дня летнего солнцестояния (22 июня), солнечные лучи, падали в глубокий колодец вертикально, достигали воды и отражались вверх. Отсюда следовало, что этот день и час Солнце в Сиене находилось в зените. Такое положение Солнца обусловлено тем, что город Сиена расположен на Северном тропике (23°,5 северной широты). Эратосфен измерил в полдень того же дня длину тени, отбрасываемой обелиском в Александрии, и нашёл, что направление солнечных лучей составляет около 7,5° с вертикалью. Затем он изготовил специальный инструмент для точного измерения углов, который он называл «скафис». С помощью этого прибора, учёный установил, что в Александрии в полдень дня летнего солнцестояния Солнце отстоит от вертикали на ¹/₅₀ долю окружности (или 7°12' в градусной мере). Так как Сиена находится на том же меридиане, что и Александрия; расстояние между городами равно длине дуги на окружности земного шара, значит, радиусы Земли в Александрии и Сиене пересекаются в центре Земли под углом 7°,2. Эратосфену была известна теорема о пропорциональности двух величин: угла с вершиной в центре окружности и дуги, отсекаемой на окружности этим углом.

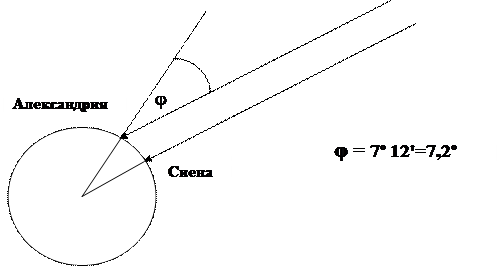Геометрическая схема измерений Эратосфена

Тогда расчет длины всей окружности Земли может быть произведён исходя из следующей пропорции:

=

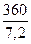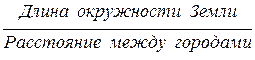
Таким образом, Эратосфен определил, что

длина окружности Земли = Расстояние между городами∙360°/7°,2

В результате Эратосфен получил длину окружности Земли в 252 тысячи стадий (39690 км). Затем по известной длине окружности он вычислил радиус Земли, получив близкое к современному значение - 6300 км(реально экваториальный радиус отличается от полярного примерно на 21 м, среднее значение радиуса Земли 6370 км).Относительная погрешность определения радиуса Земли, полученная Эратосфеном составляет менее полутора процентов. Если принять во внимание несовершенство угломерного прибора Эратосфена и неизбежные ошибки измерение расстояния шагами, то результат Эратосфена выглядит потрясающе точным! Рассчитав периметр Земли, Эратосфен был поражён тем, что известная грекам земля занимает очень небольшую часть земного шара. Эксперимент Эратосфена стал причиной настоящего переворота в географии и астрономии. Он не требует каких-либо особых условий и может быть проведён в разных точках Земли. В нём громадное расстояние до Солнца, циклический ход времени и шарообразность Земли становятся почти физически ощутимыми. Именно из-за своей красоты и изящества этот эксперимент явился значительным вкладом в человеческую культуру. В настоящее время известно, что Земля имеет форму эллипсоида вращения с неровной поверхностью, который называют геоидом. Различное значение радиуса Земли на полюсе и на экваторе впервые было установлено в XVIII веке, благодаря методу триангуляции.

6. ИСПРОЛЬЗОВАНИЕ НАУЧНОГО МЕТОДА ПОЗНАНИЯ ДЛЯ РАЗВИТИЯ ПРЕДСТАВЛЕНИЙ О МИРЕ

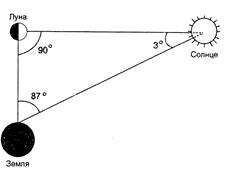Идеи александрийского астронома Аристарха Самосского (320 - 250 г.г. до н.э.), также как и идеи Архимеда, опередили своё время почти на два тысячелетия. В трактате «О размерах Солнца, Луны и расстояниях до них», Аристарх впервые в истории науки выдвинул идею гелиоцентризма, основываясь на наблюдениях, измерениях и математических расчётах. Пытаясь вычислить расстояния от Земли до Луны и Солнца, а так же оценить размеры этих светил, он установил, что Солнце значительно больше по размерам, чем Земля, а, значит, Земля не может быть центром мира. Петли планет и изменение их видимого блеска, Аристарх объяснил движением планет не только относительно Солнца, но и относительно Земли, кажущуюся неподвижность звёзд – их огромной удаленностью от Земли. Он даже допускал, что звёзды могут находиться на разных расстояниях от Земли. Но по понятным причинам доказать это не мог. Учёный полагал, что Земля вращается вокруг оси (именно по этой причине день сменяет ночь) и движется вокруг Солнца по кругу, наклонённому к земному экватору. Эти положения были несовместимы с общепризнанным учением Аристотеля. Зная величину диаметра Земли, Аристарх сумел вычислить диаметр Луны. Для этого он во время лунного затмения сравнил размер тени, отбрасываемой Землёй на Луну, с размерами лунного диска и сделал вывод, что Луна в 2,5 раза меньше Земли (на самом деле отношение экваториальных радиусов Земли и Луны равно 3,67). Расстояние до Луны учёный рассчитал, используя подобие треугольников. Для этого он заслонил диск Луны монеткой, чтобы абрис Луны совпал с кромкой монетки, и измерить расстояние от монетки до зрачка. Зная диаметр Луны можно вычислить расстояние до неё. Следующим этапом было измерение расстояния до Солнца. Для этого учёным был выбран момент, когда на небе одновременно наблюдается Луна и Солнце, причём Луна должна пребывать в первой четверти. В это время Земля, Луна и Солнце расположатся в углах прямоугольного треугольника. Для того чтобы рассчитать треугольник, нужно измерить угол между направлением на Луну и на Солнце. Этот угол, согласно измерениям Аристарха, составил 87° (современное значение 89°50΄). Тогда отношение расстояний «Земля-Луна» к расстоянию «Земля - Солнце» в современных обозначениях – Sin3° (на самом деле Sin1/7°). Из произведённых расчётов Аристарх вывел, что Солнце в 18 - 20 раз дальше от Земли, чем Луна (на самом деле после уточнений, сделанных индийскими астрономами, использующих тригонометрию - примерно в 400 раз) [7].

Используя тот факт, что визуально наблюдаемые на небе размеры Солнца и Луны приблизительно равны и во время солнечного затмения диск Луны закрывает диск Солнца, Аристарх установил, что диаметр Солнца в 6,75 раз больше земного (на самом деле в 109). Следует отметить, что измерение углов само по себе вещь очень коварная. Совсем небольшая ошибка измерения угла приводит к огромным ошибкам в вычислении сторон треугольника. Точность расчётов Аристарха была невелика, но сама идея опередила своё время. Оценить её смог только Архимед. Главное, Аристарх показал, что Солнце гораздо больше Земли, а этот вывод был важен для развития философской мысли. Кроме того, стало окончательно понятно, что мир небесных тел может быть познан с помощью наземных измерений. Вновь идея гелиоцентризма была высказана спустя 1,5 тысячелетия Н.Коперником, а сам Аристарх был обвинён в богохульстве, но последствия этого обвинения неизвестны.

Греческая планетарная теория осталась во власти представлений Пифагора и Аристотеля, согласно которым планеты движутся с постоянной скоростью по идеальным круговым орбитам. Это философское положение сохраняло свои позиции, несмотря на явные признаки переменной скорости движения планет, фактов их ретроградного движения и изменения видимой яркости. Евдокс Книдский (408 – 355 г. до н.э.) построил геоцентрическую систему мира, состоящую из 27 сфер.По три дополнительные сферы он отвёл для Солнца и Луны, по четыре для планет и сохранил большую сферу неподвижных звёзд. Позднее Апполоний Пергский (262 - 190 до н.э.) заменил сферы кругами, положив начало теории деферентов и эпициклов Птолемея. Благодаря этой уловке постоянная скорость планет преобразовывалась в наблюдаемую скорость, а планеты оставались на круговых орбитах. Вскоре выяснилось, что введённых сфер недостаточно. В итоге модель становилась всё сложнее и сложнее.

Впервые принцип равномерного движения по окружностям был поколеблен александрийским астрономом Гиппархом (190 - 126 г. до н.э.), открывшим, что длины времён года не одинаковы.Но аксиома о равномерном движении светил слишком глубоко вросла в плоть и кровь античной науки, и Гиппарх не решился её уничтожить. Чтобы объяснить свои открытия, Гиппарх допустил, что Солнце движется с постоянной скоростью по окружности, но центр этой окружности (эквант) не совпадает с центром Земли, а лежит в свободном пространстве где - то вне его.Тогда, нам действительно должно казаться, что Солнце движется неравномерно – быстрее, когда оно идёт по части круга, к которой Земля расположена ближе, и медленнее – в противоположной части. Аналогичным образом Гиппарх объяснил и движение Луны. Степень удаления центра солнечной орбиты от центра Земли была названа им эксцентриситетом орбиты Солнца. Это название удержалось в астрономическом языке до настоящего времени, и символизирует степень вытянутости орбиты планеты (или кометы).

В обсерватории на острове Родос Гиппарх вел наблюдения за звёздным небом около 40 лет. В результате уточнил координаты более 800 звёзд, представленных в шумерских таблицах и открыл явление прецессии (греч. «предварение равноденствий»). Известно, что во время весеннего равноденствия Солнце находится в определённом месте зодиака и возвращается в это положение каждый год. Учёный обнаружил, что во время следующего весеннего равноденствия Солнце находится не точно в том же участке звёздного неба, а попадает в него приблизительно на 20 секунд позднее, отставая приблизительно на 1/70°. За 26000 лет точка весеннего равноденствия обходит весь пояс зодиака. Объяснение открытому явлению было дано И.Ньютоном в XVII веке.

Гиппарх первым предложил проверить идею гелиоцентризма Аристарха Самосского наблюдениями. Движение Земли вокруг Солнца должно было вызвать параллактическое смещение звёзд, так как направление на определённую звезду будет разным, если наблюдатель располагается в разных точках земной орбиты. Но в распоряжении Аристарха были инструменты, позволяющие измерить углы с точностью не выше 1/4°, а, значит, все параллаксы звёзд оказывались равными нулю (параллакс ближайшей звезды Проксима Центавра составляет 0,′′76). Гиппарх понимал, что дело в несовершенстве инструментов и был убеждён в правоте своих предположений. Впервые техническая возможность произвести измерение параллаксов звёзд, а значит и расстояний до них, появилась только в ХIХ веке. Параллакс звезды Вега (α Лиры) составляющий 0,125'' независимо друг от друга Ф. Бессель и В. Струве (1837).

7. ГРЕКО - РИМСКИЙ ПЕРИОД РАЗВИТИЯ НАУКИ

После завоевания Египта Римом в I в. до н.э. начинается греко-римский период в развитии науки.На смену языческой культуре пришла культура христианская. Между непросвещённой массой людей и древнегреческой наукой было мало общего. Наука была аристократична от начала и до конца. Для подавляющего большинства Земля, наперекор Пифагору и Аристотелю, оставалась неподвижным плоским диском. С упадком греческой культуры и возникновением христианства, юные побеги физических знаний скоро погибнут, а сама наука придёт в забвение. Римляне возьмут из трудов древних греков только практические применения. Способность объединить простые технологии в сложные системы стало основой римского образа жизни, уровень которого был беспрецедентным для древнего мира. Римляне оставили после себя великолепное наследие и инновации, будь то архитектура или ремесло. Но в развитии науки в Древнем Риме наступила пауза, затянувшаяся в Европе на всё первое тысячелетие.

Римские энциклопедии в течение многих веков были единственным источником сведений о древнегреческой науке. Самая выдающаяся из них- «О природе вещей» Лукреция Кара (95 - 50 г. до н.э.). В ней автор изложил взгляды своих предшественников в области естествознания[8]. Несмотря на то, что прошло почти два тысячелетия с тех пор, как написана поэма, многое из того, о чём в ней говорится из области физики, принимается и современной наукой. Например, представления, лежащие в основе закона сохранения материи и движения.

За основание тут мы берем положенье такое:

Из ничего не творится ничто по божественной воле…

Лукреций критикует учения стихийных материалистов и подобно в поэтической форме излагает учение Демокрита и Эпикура.

Всю, самое по себе, составляют природу две вещи:

Это, во-первых, тела, во - вторых же, пустое пространство,

Где пребывают они, и двигаться могут различно.

При помощи этих двух предположений он объясняет «природу» вещей: плотность, упругость, способность к расширению и сжатию, к испарению и конденсации. Лукрецию ясно также и то, что движение может переходить в тепло. Этот факт использовал ещё древний человек, добывая тепло трением.

Вещи пламя дают. Разогревшись движеньем…

Становится мягким и шарик свинцовый, когда его долго катают.

В стихах Лукреция мы находим и первый закон падения тел, который Лукреций выводит из учения атомистов, которые допускали существование пустоты в природе.

Воздуха тонкая сущность

Не в состояньи вещам одинаковых ставить препятствий,

Но уступает скорее, имеющим большую тяжесть.

И далее

…Должно поэтому всё, проносясь в пустоте без препятствий,

Равную скорость иметь, несмотря на различие в весе

Другое механическое явление, известное с древности – звук, для своего распространения требует некоторого времени. Этим объясняется эхо, запаздывание громовых раскатов, по сравнению с наблюдением на небе молнии и ряд других явлений, о которых упоминает Лукреций, излагая наблюдения Аристотеля.

Гром раздаётся в ушах поздней, чем глаза различают

Молнии блеск, потому что всегда до ушей достигают

Медленней звуки, чем то, что даёт впечатление глазу.

В этом нетрудно тебе убедиться: коль издали смотрим,

Как дровосек топором двусторонним деревья срубает,

Видим мы раньше удар, а потом уже звук раздаётся

В наших ушах. Потому мы и молнию видим сначала,

Прежде, чем слышится гром, с огнём возникающий вместе.

В произведении Лукреция мы находим и учение о магнетизме. Магнит был известен ещё Фалесу. Он приписывал магниту «душу» и представлял себе, что магнитный камень «придыхает» кусок железа, и от этого притягивается к магниту. Последующие греческие философы, например Платон, познакомились и с другими свойствами магнита, в том числе с так называемым магнетизмом через влияние, которое выражается в том, что кусок железа приобретает свойства постоянного магнита от одного только его присутствия.

Мне остаётся сказать по какому закону природы

Может железо к себе притягивать камень, который

Греки магнитом зовут по названию месторожденья,

Ибо находится он в пределах отчизны магнетов.

Этому камню народ удивляется, ибо нередко

Цепью звено к звену, от него исходя, повисает.

Можно ведь видеть порой, что качаясь от лёгкого ветра,

Пять или больше таких свободно спускается звеньев.

Все они вместе висят и, одно к одному прилепляясь,

Камня силу и связь друг от друга тогда испытуют.

Лукреций упоминает, что «магнит» назван по имени города Магнезия в древней Лидии. Иначе это слово объясняет Плиний Старший, составивший другую не менее знаменитую энциклопедию - «Естественная история». Он указывает, что магнит получил своё название по имени пастуха Магнесса, заметившего, будто бы гвозди его обуви и кончик палки в некоторых местах пристают к горе Иде на острове Крит. Так или иначе, залежи магнитного железняка имеются во многих местах Земли, где они лежат вдоль магнитного меридиана. Поэма «О природе вещей» интересна нам и в другом отношении. Её автор касается не только естественнонаучных вопросов. Он рассматривает их в органической связи с общественно - гумнитарными вопросами, вопросами морали. Лукреций философствует о жизни и смерти, подчёркивает важность познания мира человеком, пишет о том, что не богатства и не власть, а знания в сочетании со здоровьем представляют собой истинные ценности.

В собственность жизнь никому не даётся.

А только на время.

Если же сердце не чисто у нас, то какие боренья,

Сколько опасностей нам угрожают тогда поневоле,

Сколько невольных забот и терзаний, внушаемых страстью,

Мучат смятенных людей и какие вселяют тревоги!

Тот же, кто в жизни себе кормилом выбрал истинный разум,

Тот обладает всегда богатством умеренной жизни;

Дух безмятежен его, и живёт он, довольствуясь малым.

Важным достижением науки греко-римского периода является уточнение солнечного календаря египетским астроном Созигеном (46 г.) и создание математической модели геоцентрической системы мира выдающимся учёным астрономом и математиком Клавдием Птолемеем (100-165). Система мира К.Птолемея, которая царила, не оспариваемая никем, около полутора тысяч лет, была основана на наблюдениях и вычислениях Гиппарха и его представлении об экванте (смещении положения Земли относительно центра орбиты Солнца). Модель Птолемея, безусловно, самая успешная попытка создания прогнозируемой астрономии. Она воспроизводила видимое движение планет, включая ретроградные петли. Любое несоответствие в измерениях обычно не выходило за пределы погрешности методов измерения.

Птолемей изложил свою систему мира в сочинении «Мегале синтаксис» («Великое построение»), более известном под арабским названием «Альмагест». До конца средневековья этот труд почитался наравне с божественным откровением. Сомнения в словах «Альмагеста» считалось преступлением.

В основе системы мира Птолемея лежат четыре постулата:

-Земля находится в центре Вселенной.

-Земля неподвижна.

-Все небесные тела движутся вокруг Земли.

-Движение небесных тел происходит по окружностям с постоянной скоростью, то есть равномерно.

В подтверждение этих положений в «Альмагесте приводились достаточно веские физические доводы:

-небесные полюсы неподвижны;

-звёзды не удаляются и не приближаются к Земле;

-облака мы видим расположенными по всему небу, а не только на западе, куда их относило бы вследствие вращения Земли;

-тела, брошенные отвесно вверх падают в том же месте.

Опровергнуть эти доводы на основе физики Аристотеля было практически невозможно.

В основу своего построения Птолемей положил эксцентрические круги Гиппарха и конструкцию деферентов-эпициклов Аполлония Пергского.Согласно Птолемею, все планеты за исключением Солнца, не обращаются непосредственно по деферентам (deferens – лат. «несущий») – по ним движется центр другого круга эпицикла (kiklos –греч. «над»), и только по нему обращается планета. Для каждой планеты Птолемей подобрал относительные размеры радиусов эпицикла и деферента, положения центров деферентов и скорости движения планет по эпициклам и деферентам так, чтобы движение получилось близким к реально наблюдаемому. Система мира Птолемея не только давала качественное объяснение видимым движениям планет, но и позволяла вычислять их положение на будущее с довольно высокой точностью. По мере повышения точности возникали разногласия с теорией, которые устранялись путём очередного усложнения системы. Когда предлагаемое построение для какой - либо планеты оказывалось недостаточным, вводили третий, четвёртый и т.д. эпициклы, пока положение планеты на окружности последнего из них не давало согласия с наблюдением. Интересно и то, что сам К.Птолемей в конце жизни осознавал, что его система мира имеет какой-то изъян, и, возможно, даже догадывался какой. Он писал: «Легче, кажется, двигать сами планеты