Решение систем нелинейных и трансцендентных уравнений
Функция solve применяется и для решения систем нелинейных и трансцендентных уравнений. Для этого и система уравнений и перечень неизвестных задаются в виде множеств.
> restart
> solve({x*y=3,x-y=1},{x,y});
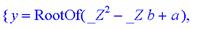
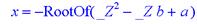
> allvalues(%);
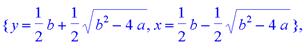
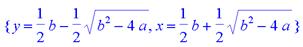
> restart;
> s:=solve({x*y=2,x+y=3},{x,y});
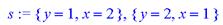
> assign(s);x;y;
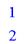
Решение неравенств
Решение неравенств существенно расширяет возможности функции solve. При этом неравенства задаются так же, как и равенства. Приведенные примеры поясняют технику решения.
> restart;
> solve(x^2-2*x-3>0,x);
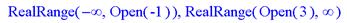
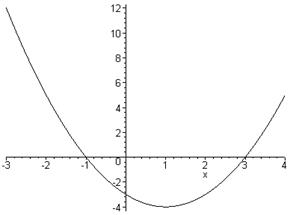
> plot(x^2-2*x-3,x=-3..4,color=black);
> restart;
> solve((x-1)*(x-2)/(x-3)<1,x);
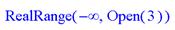
> plot((x-1)*(x-2)/(x-3),x=-3..5,y=-3..2,color=black);
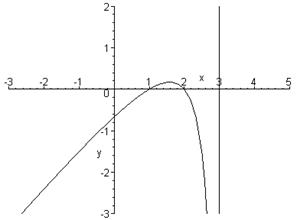
Из приведенных примеров очевидна форма решений – представлены критические значения аргумента, вплоть до не включаемых значений области действия неравенства (они указываются словом Open). Всегда разумно построения графика выражения, которое задаёт неравенство, это позволяет наглядно убедиться в правильности решения.
Приведём примеры решения неравенств в аналитическом виде:
> solve(5*x>10,x);

> solve(5*x>=10,x);

solve({x+y-z>0,x>-1,y+z>10},{x,y,z});
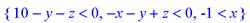
> evalf(%);
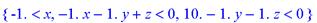
Дата добавления: 2020-10-01; просмотров: 618;











