Идеальный трубчатый реактор полного вытеснения (ТРПВ)

Если при течении жидкости по трубопроводу сравнительно большого диаметра или по каналу число Рейнольдса достаточно велико (например, больше 2100 для трубы), то течение в такой системе приближается к режиму полного вытеснения (поршневому потоку), при котором в поперечном сечении потока осевые скорости не изменяются. Если допустить, что режим полного вытеснения приближенно описывает движение жидкости через реактор, то, воспользовавшись понятием об элементарном объеме, можно вывести уравнения материального баланса по компонентам системы в трубчатом реакторе полного вытеснения (ТРПВ). Как показано на рис. 9.5, при таком подходе принимается, что в трубчатом реакторе стационарное состояние сохраняется в элементарном объеме потока, перпендикулярном оси реактора. Материальный баланс по некоторому произвольному компоненту С в элементарном объеме можно выразить следующим уравнением:

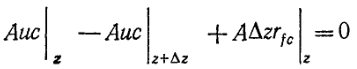(13)

Здесь r_fc — скорость образования компонента С, выраженная через его количество в единице объема за единицу времени.

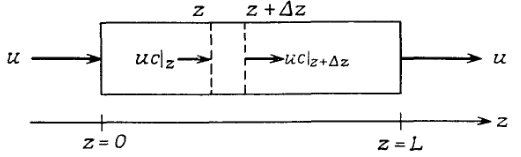
РИС. 5. Реактор полного вытеснения.

Преобразование и деление на AΔz дает

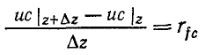(14)

Вспомнив определение производной, нетрудно найти, что в пределе это уравнение преобразуется, давая в окончательном виде

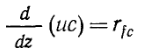(15)

Если в результате реакции плотность жидкости не изменяется (справедливо ли это допущение для микробиологического процесса?) и если осевая скорость постоянна, то уравнение (9.15) принимает вид:

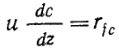(16)

Величина z/u равна времени, которое затрачивает элементарный объем жидкости на движение от входа в реактор до осевого положения z. Если в качестве новой независимой переменной использовать время движения элементарного объема t, равное

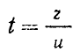(17)

то уравнение материального баланса по компоненту C примет вид:

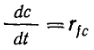(18)

Последнее уравнение полностью совпадает с уравнением материального баланса по компоненту C в реакторе периодического действия. Приведенное выше математическое доказательство можно дополнить следующей аргументацией: в режиме поршневого потока при постоянной скорости каждый элементарный объем жидкой фазы движется вдоль трубчатого реактора без какого-либо взаимодействия с соседними объемами. Следовательно, система полностью сегрегирована, и каждый элементарный объем ведет себя как реактор периодического действия. Отсюда следует, что если исходная смесь в реакторе периодического действия имеет тот же состав, что и смесь, подаваемая в реактор полного вытеснения, и если среднее время пребывания L/u в последнем равно времени реакции в реакторе периодического действия, то и вытекающая из трубчатого реактора масса будет идентична по своему составу продукту в реакторе периодического действия. Этой модели отвечает граничное условие

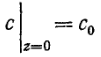(19)

Здесь z=0 отвечает точке ввода исходных веществ в реактор, а c₀ — концентрация компонента C в исходной смеси.

Допустим, например, что кинетика процесса в хемостате Моно не отличается от кинетики процесса в ТРПВ (или в эквивалентном реакторе периодического действия). В этом случае уравнения материального баланса по клеточной массе и субстрату [уравнение (9.18)] преобразуются следующим образом;

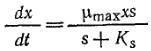(9 20)

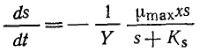( 21)

С начальными условиями

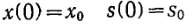(22)

Логическим путем или посредством преобразования уравнений (9.20) и (9.21) нетрудно найти, что концентрации s и х: связаны стехиометрически

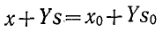(.23)

Если при помощи уравнения (23) выразить x через s и подставить полученное выражение в уравнение (9.21), то мы получим обычное дифференциальное уравнение:

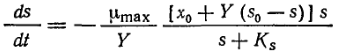(24)

Это уравнение при условии (9.22) можно интегрировать аналитическим путем; тогда получим:

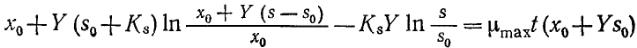(25)

Концентрации субстрата на выходе из реактора отвечает значение s при t=L/u-, соответствующее значение х легко найти с помощью уравнения (.23). Если считать, что уравнение (9.20) описывает кинетику периодического процесса, нетрудно видеть, что эта математическая модель не учитывает лаг-фазу и фазу отмирания клеток, но отражает стационарную фазу клеточного роста.

В отличие от ПРПП стерильность исходных веществ в ТРПВ автоматически предполагает и нулевую концентрацию биомассы на выходе из реактора, поскольку поршневой характер потока предотвращает инокуляцию движущегося по трубчатому реактору элементарного объема жидкости. Этот недостаток можно устранить, например, путем предварительной инокуляции поступающего в реактор потока исходных веществ.

Не представляет затруднений интегрирование уравнений материального баланса по отдельным компонентам в реакторе полного вытеснения; таким образом можно получить выражения, описывающие связь между концентрациями компонентов в продуктах и общим временем пребывания в реакторе L/u для некоторых обычных реакций, катализируемых ферментами. Результаты таких расчетов приведены в табл. 2.

Сравнительные характеристики идеальных ПРПП и ТРПВ зависят от типа осуществляемых в них реакций и их кинетики. При протекании одностадийной реакции с обычной кинетикой (когда скорость реакции снижается при увеличении превращения субстрата; примером могут служить реакции, описываемые уравнением Михаэлиса — Ментен) ТРПВ обеспечивает более высокую степень превращения субстрата и большую концентрацию продукта реакции на выходе из реактора по сравнению с ПРПП равного объема.

Для автокаталитических реакций (когда скорость реакции возрастает при снижении концентрации субстрата) справедливо обратное соотношение характеристик ТРПВ и ПРПП. В микробиологических процессах ТРПВ обычно обеспечивает большую концентрацию продукта в вытекающем из реактора потоке.

В то же время необходимость непрерывного внесения посевного материала и ряд затруднений технического характера при осуществлении газового обмена в ТРПВ часто приводят к тому, что на практике выгоднее применять аналогичные реакторы периодического действия, даже если высокая концентрация продукта в вытекающем из реактора потоке является важным фактором.

В фазе экспоненциального роста ПРПП эффективнее ТРПВ или реакторов периодического действия. Сравнительное изучение идеальных ТРПВ и ПРПП при их использовании для различных простых сочетаний реакций составляет основную тему учебных пособий по химической технологии, перечисленных в списке литературы в конце этой главы. С другими примерами сравнительного изучения различных реакторов мы познакомимся в упражнениях.

Таблица 2. Взаимосвязь между степенью превращения субстрата δ=(s₀-s)/s₀ и важнейшими параметрами ферментативных реакций в ТРПВ^a. Данные относятся к ферментам в растворе или к гранулам иммобилизованных ферментов с пренебрежимо малым сопротивлением массопередаче; для ферментов в растворе выражение (1—ε)/ε равно единице