Поиск по критерию близости к цели

Критерием близости к цели обычно является числовая функция h(b)>=0 , вычисляемая для вершины b и характеризующая близость этой вершины к целевой. При использовании критерия близости к цели, начиная с корневой вершины, просматриваются все соседние ей вершины, выбирается та, для которой h(b) минимальна, и все повторяется вновь для выбранной вершины.

И так до тех пор, пока не будет достигнута целевая вершина, для которой h(b)=0, т.е. выбирается та вершина, которая ближе всего находится к цели. Вид критерия близости к цели зависит от среды (является проблемно зависимым). Чтобы получить достаточно полное представление об этом критерии, вернемся к задаче поиска маршрута из Иванова в Москву. Критерием выбора в этом случае будет минимальное расстояние по прямой (кратчайшее расстояние) от вершины (населенного пункта) до Москвы. Естественно, чтобы значение критерия могло быть вычислено, необходимо иметь карту или какой-либо другой источник информации, содержащий сведения о кратчайших расстояниях от населенных пунктов до Москвы. На рис. 4.5 показана последовательность поиска по критерию близости к цели для примера с поиском маршрута из Иванова в Москву, использованного при рассмотрении монотонного поиска в ширину.

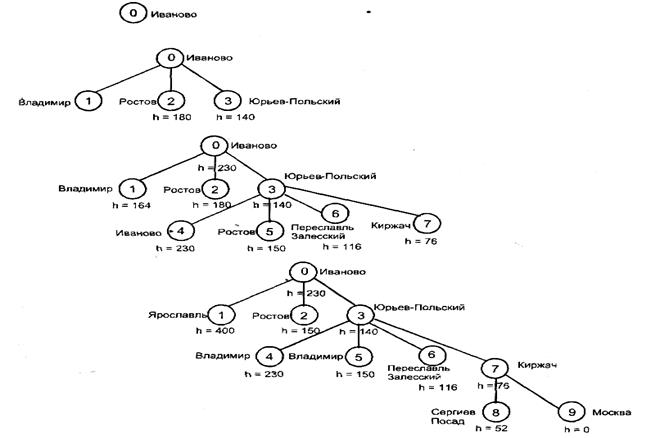Рис. 4.5. Поиск по критерию близости к цели

На первом шаге вычисляется кратчайшее расстояние от корневой вершины (Иваново) до Москвы (h=230). На втором шаге просматриваются все вершины (города), в которые ведет дорога из Иванова и вычисляется кратчайшее расстояние h от этих городов до Москвы. По этому критерию ближайшим по прямой до цели (Москвы) оказывается Юрьев-Польский (h=140). На третьем шаге просматриваются все вершины, в которые ведет дорога из Юрьева- Польского.

Для них снова вычисляется кратчайшее расстояние h до Москвы, кратчайшим оказывается расстояние от Киржача (h=76). Наконец, на последнем шаге вновь просматриваются все вершины, в которые ведет дорога из Киржача, а также вычисляется кратчайшее расстояние до этих городов. Среди этих городов оказывается город с кратчайшим расстоянием h=0, т.е. целевая вершина (Москва).

На этом поиск по критерию близости к цели завершается. Поиск по критерию близости к цели является поиском в глубину, но с выбором на каждом шаге единственной вершины, от которой начинается следующий шаг.

Недостатки этой стратегии те же, что и для слепого поиска в глубину, а именно, она неоптимальная и неполная, поскольку может случиться, что поиск пойдет по бесконечному пути и никогда не вернется назад. Оценка сложности по времени этой стратегии поиска равна 0(l^d), где d – максимальная глубина пространства поиска. При поиске по критерию близости к цели приходится хранить все вершины, рассматриваемые при поиске. Поэтому оценка сложности по памяти для этой стратегии та же, что и оценка сложности по времени. Если критерий близости к цели выбран достаточно удачно, то сложность поиска может быть существенно уменьшена.

4.3.2. Поиск по критерию цены пути (А*-поиск)

С помощью этого критерия можно находить пути с минимальной ценой.

Обозначим g(b) – критерий цены пути из корневой вершины в вершину b, a h(b) – уже рассмотренный критерий близости к цели. Пусть оба критерия имеют одну и ту же размерность. Функцию f(b)=g(b)+h(b) можно считать критерием цены пути из корневой вершины в целевую.

Рассмотрим стратегию поиска на основе этого критерия и покажем, что она будет полна и оптимальна, если ввести небольшие ограничения на критерий h(b).

Идея этого ограничения состоит в том, чтобы выбирать критерий h(b) таким образом, чтобы не переоценивать близость к цели, т.е. не выбирать значение h(b) меньше, чем оно есть на самом деле. Критерий h(b), выбираемый таким образом, называется допустимым. Стратегия поиска, использующая критерий f(b) и допустимый критерий h(b), известна как А*-поиск. Критерий близости цели h(b), использованный в примере с поиском маршрута из Иванова в Москву, является типичным примером допустимого критерия, поскольку не может быть пути из одного населенного пункта в другой короче, чем кратчайший путь. На рис. 4.6 показаны первые четыре шага поиска пути из Иванова в Москву с использованием критерия f(b) в А*-поиске. Заметим, что в результате этого поиска, в отличие от поиска только по критерию близости к цели, рассмотренного в предыдущем разделе, выбран путь к Москве не через Юрьев-Польский, а через Владимир, хотя Юрьев-Польский ближе к Москве, чем Владимир. Такой выбор объясняется тем, что цена пути g(b) от Иванова до Юрьева-Польского выше, чем до Владимира вследствие очень плохой дороги.

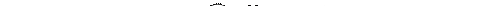
Дальнейший выбор маршрута можно проследить по рисунку, где на любом пути от корневой вершины значение критерия f(b) нигде не уменьшается при переходе к рассмотрению очередной вершины. Это не случайность и справедливо почти для всех допустимых критериев h(b) близости к цели. Критерии f(b), для которых имеет место подобное свойство, называются монотонными. Если монотонность нарушается, то путем незначительной коррекции это нарушение может быть устранено. Рассмотрим, например, пару вершин b, b', где b предшественник, а b' – последователь. Предположим, что g(b)=3, h(b)=4. Тогда f(b)=7, т.е. цена пути через вершину b самое меньшее равна 7. Предположим также, что g(b')=4, h(b’)=2, т.е. f(b')=6. Ясно, что в этом случае критерий f(b) не является монотонным. К счастью, благодаря тому, что любой путь через b’ является также путем через b, цена пути f(b')=6 является бессмысленной. Поэтому каждый раз, как рассматривается какая-либо вершина b' и оказывается, что ее цена пути f(b')<f(b), мы полагаем, что f(b') =f(b), т.е. f(b')=max (f(b), f(b')).

Таким способом немонотонность может быть всегда устранена, и критерий f(b) никогда не будет уменьшаться вдоль одного и того же пути при условии, что h(b) допустимое. Если же f(b) никогда не уменьшается вдоль одного и того же пути, начинающегося от корневой вершины, то на пространство состояний можно наложить контуры, каждый из которых охватывает множество вершин b, для которых значение критерия f(b) меньше определенной величины с. Процесс поиска можно представить как переход от просмотра еще не просмотренных вершин какого-либо внутреннего контура, для всех вершин b₁ которого имеет место f(b₁) < с, к просмотру вершин некоторого внешнего контура, для всех вершин b ₂ которого имеет место f(b₂)<с₂ и с₁<с₂. Это продолжается до тех пор, пока внутри очередного контура не окажется целевая вершина с h(b)=0. При удачном выборе критерия f(b) контуры как бы растягиваются в сторону целевой вершины, фокусируясь вокруг оптимального пути. Обозначим с* цену оптимального пути. Тогда можно утверждать следующее:

А*-поиск просматривает вершины с f(b)<=с*.

А*-поиск осуществляет направленный просмотр вершин, стремясь к просмотру вершин контура, для которых имеет место f(b)=с*.

Решение, получаемое с помощью А*-поиска, является оптимальным, поскольку находится вершина с максимальным значением f(b), a следовательно, и максимальным g(b), так как h(b)=0. А*-поиск является также полным, поскольку, увеличивая постепенно значение критерия f(b), мы должны, в конце концов, найти путь к целевой вершине. Заметим также, что для данного критерия f(b) не существует никакой другой процедуры поиска, которая давала бы более оптимальные решения, чем А*-поиск. Все эти утверждения требуют более строгих доказательств, которые мы здесь не приводим. Оценки сложности по времени и памяти для А*-поиска аналогичны оценкам для поиска по критерию близости цели.

На идее А*-поиска построено много других методов поиска, учитывающих особенности конкретной среды, которые влияют на выбор критериев, и различные ограничения, например по доступным ресурсам (времени выполнения и доступной памяти).