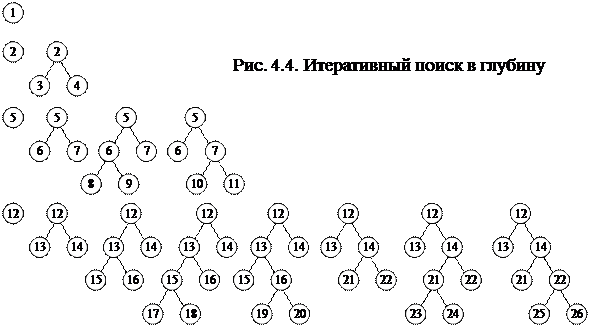
Итеративный поиск в глубину
При ограниченном поиске в глубину сложность поиска зависит от выбора ограничения. Например, при поиске маршрута можно использовать не число всех населенных пунктов в районе поиска подходящего маршрута, а максимальное число населенных пунктов, которые могут встретиться на каждом из возможных маршрутов. Это число называют обычно радиусом поиска. Знание радиуса поиска приводит к более эффективному ограниченному поиску в глубину. Однако в большинстве задач радиус поиска не известен до тех пор, пока задача не будет решена. Итеративный поиск в глубину использует стратегию, основанную на итеративном применении ограниченного поиска в глубину сначала для радиуса поиска, равного 0, затем 2, после этого 3 и т.д. Четыре итерации такого поиска для бинарного дерева иллюстрирует рис. 4. 4. Итеративный поиск в глубину может показаться очень неэффективным, поскольку некоторые вершины просматриваются многократно. Однако для многих задач подавляющая доля вершин находится на низком уровне. Напомним, что оценка сложности по времени при ограниченном поиске в глубину вычисляется по формуле
0(lk)=1+1+l2…+lk-2+lk-1+lk
Например, для l = 10, k = 5 будем иметь 0(l k) = 111111. При итеративном поиске на глубину k вершины глубины k просматриваются один раз, глубины k-1 — два раза, глубины k-2 — три и т.д. Корневая вершина просматривается k + 1 раз.
 |
Таким образом, оценка сложности по времени при итеративном поиске в глубину вычисляется по формуле
0(lk)=(k+1)l0+(k)l1+(k-1)l2+ …+3lk-2+2lk-1+1lk
Для l=10, k=5 будем иметь 0(lk)=123456. По сравнению с оценкой сложности по времени для ограниченного поиска в глубину сложность по времени для итеративного поиска в глубину возросла только на 11%. Из формулы, приведенной выше, видно, что чем выше степень ветвления, тем ниже доля сложности, получающейся за счет повторного просмотра вершин. Но даже для случая, когда l=2, сложность по времени итеративного поиска в глубину только в два раза превосходит сложность по времени простого поиска в глубину. Это означает, что оценка сложности по времени итерационного поиска в глубину по-прежнему равна O(lk), а сложность по памяти – O(lk). Итеративный поиск в глубину достаточно хорошо себя зарекомендовал для задач с большим пространством поиска и неизвестной его глубиной. Если цена данного пути меньше цен всех этих путей, то поиск вершин на этом пути продолжается. В противном случае поиск вершин на этом пути откладывается, а продолжается поиск вершин на путях, цена которых меньше данного. Когда на каком-либо пути будет достигнута целевая вершина, поиск на путях, цена которых.
Дата добавления: 2020-08-31; просмотров: 591;











