Рассуждения в пространстве состояний среды.
В коммунальной квартире две старушки занимают по комнате. Комнаты находятся в общем коридоре, который имеет выход на лестничную клетку. Одна из комнат расположена слева (левая комната) от выхода, а другая – справа (правая комната). В коридоре живет кот, которого обе старушки одинаково любят и балуют, оставляя ему кусочки сыра. Каждая старушка кладет кусочек сыра у двери своей комнаты. Кот отдыхает либо у левой комнаты (слева), либо у правой (справа).
Множество всех состояний этой среды (среды кота) можно представить табл. 3.1, в столбцах которой для каждого состояния среды указаны - местонахождение кота (слева или справа), наличие или отсутствие кусочка сыра (да или нет) у соответствующей комнаты.
| Таблица 3.1 | |||
| Состояние | Местонахождение кота | Наличие сыра | |
| слева | справа | ||
| b1 | Слева | Да | Да |
| b2 | Справа | Да | Да |
| b3 | Слева | Да | Нет |
| b4 | Справа | Да | Нет |
| b5 | Слева | Нет | Да |
| b6 | Справа | Нет | Да |
| b7 | Слева | Нет | Нет |
| B8 | Справа | Нет | Нет |
Состояние b1 означает, что кот находится около левой комнаты и около обеих комнат лежит по кусочку сыра, состояние b2 — кот находится около правой комнаты и около обеих комнат снова лежит по кусочку сыра и т.д.
Кот может совершать в один и тот же момент времени только одно из следующих действий: переходить к дверям левой комнаты, переходить к дверям правой комнаты и съедать кусочек сыра около той комнаты, где он находится.
Эти действия обозначим с1=Идти налево, с2=Идти направо и с3=Съесть, соответственно. Если среда находится в одном из состояний, перечисленных в табл. 3.1, и кот совершает какое-либо из действий, то нетрудно определить в какое состояние после выполнения действия перейдет среда.
Будем полагать, что нам известно состояние, называемое начальным, с которого могут начаться изменения среды при действиях кота.
Пусть, например это будет состояние b1. Будем изображать состояния кружочками с обозначением состояния внутри кружочка.
Переход из одного состояния в другое, происходящий в результате действия, будем изображать стрелкой, ведущей в это другое состояние и помеченной соответствующим действием. Так, на рис.3.1 изображены все переходы из состояния b1 в результате действий с1,с2 , с3 .
На рис. 3.2 показано дерево всех дальнейших переходов, являющееся продолжением элементарного дерева на рис. 3.1. Построение каждой ветви дерева прекращено на том состоянии, которое встречается повторно на пути, ведущем в него из начального состояния.
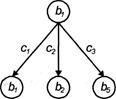 |
Рис. 3.1. Допустимые переходы из начального состояния b1
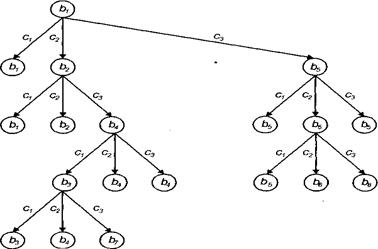
Рис. 3.2. Дерево переходов
Постановка задачи
Цель кота — не оставить ни одного кусочка сыра, где бы он изначально ни находился. В терминах состояний среды целью кота является перевод ее с помощью своих действий (реакций) в одно из состояний b7 или b8. Состояния, в которые с помощью набора допустимых действий необходимо перевести среду, называются целевыми. Процесс определения этих состояний называют формулировкой цели. Будем полагать в рамках нашего примера, что каждое восприятие совпадает с одним из состояний. Задачей агента является нахождение последовательности действий или пар восприятие – действие, ведущих на дереве переходов из начального состояния в целевые. Процесс нахождения этих последовательностей называют поиском, выводом или рассуждением. Постановкой задачи называют задание всех состояний и действий, которые можно использовать для решения задачи, начального состояния и целевых состояний, а также всех допустимых переходов между состояниями при выполнении действий. Для среды кота постановка задачи уже осуществлена. Все состояния, которые могут использоваться при решении задачи, перечислены в табл. 3.1. Целевыми состояниями являются состояния b7, b8. Все допустимые переходы между состояниями показаны на рис. 3.2. Из рисунка ясно, что решениями задачи является последовательность b1/c2, b2/c3,b4/c1,b3/c3, в результате выполнения которой агент (кот) переведет среду в состояние b7, и последовательность b1/c3, b5/c2, b6/c3, в результате выполнения которой среда окажется в состоянии b8.
Дата добавления: 2020-08-31; просмотров: 666;











