Загальні зауваження

Кристалічна гратка твердих тіл представляє самий наочний об'єкт, який природно назвати упорядкованою структурою з осциляторів (коливальних елементів). Найпростішими прикладами моделі впорядкованої структури, в якій тотожні осцилятори пов'язані між собою не будь-яким, а певним чином, є одномірна гратка з однакових частинок, механічна система, що складається з набору маятників, ланцюжок пов'язаних електричних контурів, ряд однакових акустичних резонаторів, ланцюжок, утворений з магнітів і т. п.

Таким чином, ми переходимо до розгляду систем з N ступенями свободи, причому N може бути дуже великим і навіть «нескінченно великим» числом. Кожній ступені свободи відповідає своя власна частота і форма коливань. Часто їх називають модами коливань. Якщо вивести один елемент такої системи з положення рівноваги, то будуть зміщуватися і сусідні - по всій впорядкованій структурі побіжить «хвиля». Іншими словами, при дуже великому числі елементів у системі (у межі нескінченно великому), укладених в обмеженому обсязі, вона веде себе як безперервне середовище. 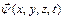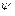Таке твердження має на увазі, що зміщення всіх елементів в околиці точки може бути описано вектором зміщення , де - безперервна функція. Ця функція замінює опис, що задає зміщення 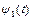, 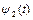і т.п. окремих елементів. У такому випадку говорять про поширення хвилі. Тут слід пам'ятати, що координати x, y, z відповідають рівноважного стану частинок і не залежать від часу.

Як приклад розглянемо моди коливань струни з вантажами. Під «струною» вважаємо невагомі пружини, на яких розташовані точкові маси. Послідовність таких струн показана на рис. 7.1, що дозволяє легко зрозуміти конфігурації і частоти мод.

Рисунок 7.1– Різні конфігурації і частоти мод коливань