Химический потенциал.

Реальный газ. Фактор сжимаемости природных газов. Вириальное уравнение состояния, уравнение Майера - Боголюбова. Уравнение Ван – дер - Ваальса.

Для реальных газов уравнение состояния 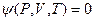в общем виде записывается так

,

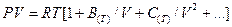где 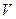– мольный объём газа; 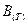, , 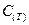… - второй, третий и т.д. вириальные коэффициенты. Само уравнение называется вириальным уравнением состояния(Каммерлинг – Онесс).

Принципиально можно теоретически рассчитать вириальные коэффициенты с той или иной степенью точности. Но это довольно сложная проблема, которая в конце курса ещё будет затронута.

Вычислив 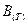, , 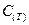…, получим уравнение состояния для конкретного газа.

Лучше было бы получить уравнение состояния, которое описывало поведение всех реальных газов, несмотря на потери в точности.

Впервые эту задачу решил голландский физик Ван-дер-Ваальс в своей диссертации "Непрерывность газообразного и жидкого состояния" (1873 г.). Такое уравнение состояния должно учитывать взаимодействие молекул, т.е. силы притяжения и отталкивания между молекулами.

Простые и не очень строгие рассуждения привели к уравнению вида

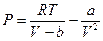или (*)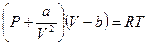

Уравнение называется уравнением состояния Ван-дер-Ваальса.Вывод сделан на основе качественных рассуждений о молекулярном объёме "b" и межмолекулярных силах притяжения, величина которых пропорциональна квадрату плотности газа. Но в этом и сила этого подхода. Не надо точно знать, что происходит между молекулами. К величинам "а" и "b" можно относиться как к подгоночным параметрам. А сходство реальных изотерм в Р, V – диаграмме с изотермами Ван-дер-Ваальса говорит о силе этого уравнения (см. рис.).

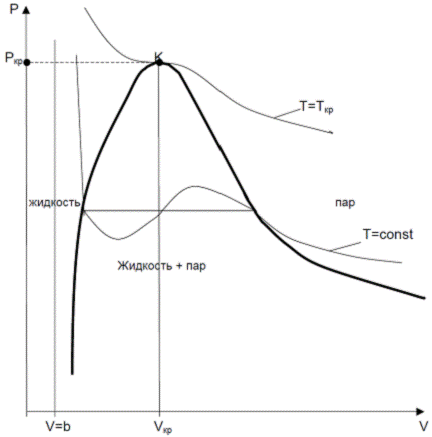
Кривая насыщения и изотермы Ван-дер-Ваальса в Р-V диаграмме.

Когда молекула газа летит к стенке, а затем отражается от неё, то меняется её импульс. Ежесекундное изменение импульса всех молекул, падающих на единицу площади стенки и отражающихся от неё равно . Однако, в отличие от идеальных газов, импульс налетающих молекул изменяется не только под действием сил давления со стороны стенки, но и под действием сил, с которыми их тянут внутрь газа молекулы пристеночного слоя. В частности, под действием этих последних сил молекула может отразиться внутри пристеночного слоя, не долетев до стенки.

(*)

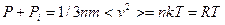Давление на стенку 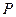не зависит от материала стенки. Роль стенки может выполнять сам газ. Проведём мысленно произвольное сечение, разделяющее газ на две части. Давление одной части на другую будет таким же, как если бы эта другая часть была твёрдой стенкой. Оно равно 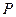, а не 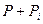или какой-либо другой комбинации этих величин. Именно это давление 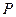входит в уравнение гидродинамики и газодинамики.

Сила 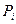называется внутренним или молекулярным давлением. Её можно представить в ви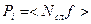де , где 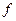- сила, действующая на молекулу пристеночного слоя, а 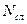- число молекул в нём, отнесённое к единице площади. Можно также написать 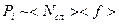. Обе величины 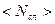и 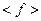пропорциональны плотности или обратно пропорциональны объёму газа. Предполагая, что газ взят в количестве одного моля, можно положить

,

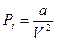где 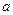- постоянная, характерная для рассматриваемого газа. Тогда (*) переходит в

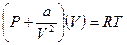
Учтём совместное действие сил притяжения и сил отталкивания. Для неплотных газов поправки на силы притяжения и отталкивания можно вводить независимо. Так как объём, доступный движущимся молекулам, будет равен 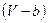, то:

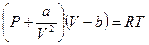
После раскрытия скобок уравнение изотермы примет вид.

(**)

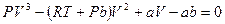Это уравнение третьей степени по 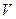, в которое давление 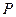входит в качестве параметра. Поскольку его коэффициенты вещественны, уравнение имеет либо один вещественный корень, либо три корня. Каждому корню на плоскости ( 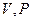) соответствует точка, в которой изобара 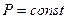пересекает изотерму. В первом случае, когда корень один, и точка пересечения будет одна. Так будет при любых давлениях, если температура достаточно высока. Изотерма имеет вид монотонно опускающейся кривой. При более низких температурах и надлежащих значениях давления уравнение имеет три корня 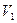, 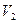и 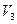. В таких случаях изобара 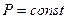пересекает изотерму в трёх точках. Изотерма содержит волнообразный участок. При некоторой промежуточной температуре три корня 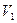, , 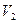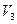становятся равными. Такая температура и соответствующая ей изотерма называются критическими. Критическая изотерма всюду монотонно опускается вниз, за исключением одной точки 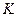, являющейся точкой перегиба изотермы. В ней касательная к изотерме горизонтальна. Точка 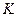называется критической точкой. Соответствую ей давление 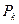, объём 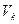и температура 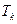называются также критическими, а вещество находится в критическом состоянии.

В критической точке

,

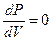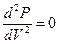
Решая эти уравнения, можно выразить критические параметры через постоянные Ван-дер-Ваальса "а" и "b":

, , . (**)

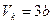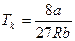Из уравнений (**) следует, что фактор (коэффициент) сжимаемости

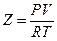
в критической точке согласно уравнению Ван-дер-Ваальса одинаков для всех веществ и равен

.

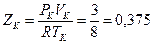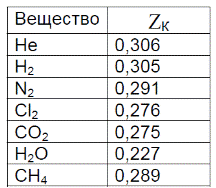
Величина фактора сжимаемости в критической точке некоторых реальных газов приведена в таблице. Как правило эти величины меньше 0,375 и отклонения возрастают для полярных молекул.

Таблица. Значения критического фактора сжимаемости ZK реальных газов.

Ван-дер-Ваальс предложил также ввести приведённые переменные газа:

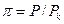– приведённое давление;

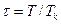– приведённая температура;

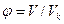– приведённый объём.

Была надежда на то, что при одинаковых приведённых температурах и объёмах различные реальные газы будут оказывать одинаковое приведённое давление. Обратимся к уравнению (*). Если в него вместо 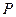подставить 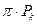, вместо 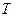– 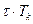τ⋅ТК , вместо 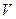– 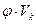, и выразить значения критических параметров из уравнений (**) то получим

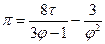или (**)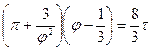

Это уравнение имеет ту же форму, но константы "а" и "b", характеризующие тот или иной газ, в нём исчезли. Таким образом, уравнение (2.47) справедливо для всех реальных газов, подчиняющихся уравнению состояния Ван-дер-Ваальса. Теория соответственных состояний, как часть теории термодинамического подобия, построена на этом уравнении. Термодинамические свойства веществ в соответственных состояниях одинаковы. Это утверждение теории является мощным инструментом для предсказаний неизвестных

свойств.

Пограничные кривые, критические параметры. Метастабильные и лабильные состояния. Фазовая диаграмма давление – температура чистых веществ, фазовые диаграммы плотность - температура, давление - удельный объем чистых жидкостей. Соответственные состояния, критический коэффициент сжимаемости.

Сейчас начнём обсуждать фазовое поведение флюидов в свободном (без пористой среды) объёме.

Фазовые превращения вещества – широко распространённое явление в природе. простейшими их примерами служат превращение перегретой жидкости в пар, кристаллизация жидкости, выпадение растворённого вещества из пересыщенного раствора. Приведенные примеры относятся к фазовым превращениям первого рода.

Фазой называется макроскопическая физически однородная часть вещества, отделённая от остальной части системы границами раздела, так что она может быть извлечена из системы механическим путём.

К концу XIX столетия физико-химикам казалось, что всё многообразие фазовых равновесий исчерпано в следующих типах равновесий: кристалл – кристалл, кристалл – жидкость, кристалл – газ, жидкость – жидкость и жидкость – газ. Теория этих фазовых равновесий была изложена в работах Коновалова, Столетова, Гиббса, Ван-дер-Ваальса, Куэнена и др. Существовало и убедительное подтверждение теоретических представлений.

Сейчас нам кажется странным, почему возможность существования ещё одного типа равновесий – равновесие между двумя газовыми фазами (наличие которого можно было предположить хотя бы по простой аналогии) вообще не обсуждалась до самого конца XIX столетия.

Термодинамические диаграммы, в которых по осям координат откладываются давление, температура, мольный объём и наносятся кривые фазового равновесия называются фазовыми диаграммами. Для многокомпонентных систем по осям координат может откладываться и состав.

Кривой фазового равновесия называется линия на фазовой диаграмме, соответствующая состояниям равновесия сосуществующих фаз.

Что такое равновесие?