Термодинамические потенциалы и характеристические функции.

Фундаментальное уравнение термодинамики для закрытых систем, в которых не идут химические реакции

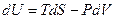
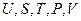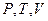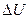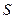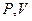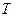В это уравнение входят пять переменных . Три величины можно измерить. Изменение внутренней энергии можно измерить при условии постоянства объёма. Энтропия не может быть непосредственно измерена, но может быть рассчитана, если известны остальные величины. Параметры и связаны между собой термическим уравнением состояниявида

.

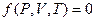поэтому можно выбрать только два независимых параметра.

Внутренняя энергия может быть выражена через термические параметры с помощью калорического уравнения состояниявида

.

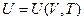Оба уравнения состояния системы выбираются на основании экспериментальных данных или теоретических представлений.

Построениекалорического уравнения состояния на основе измерения теплоёмкости.

Теплоёмкость.

Теплоёмкость тела С называется отношение бесконечно малого количества тепла 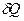, полученного телом, к соответствующему приращению 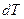его температуры:

.

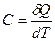Когда масса тела равна единице, теплоёмкость называется удельной. Более удобна молярная теплоёмкость – теплоёмкость одного моля вещества.

Приращение температуры 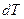не определяет ещё полностью того бесконечно близкого состояния, в которое переходит система из заданного состояния.

Рассмотрим, например, физически однородное тело, состояние которого полностью определяется двумя параметрами, в качестве которых можно взять объём и температуру.

Пусть исходное состояние изображается точкой 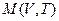(см. рис.). Проведём прямую , параллельную оси объёмов и отстоящую от точки 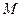на величину 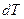. Все точки этой прямой изображают состояния с одной и той же температурой 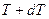, но с различными объёмами. Система из состояния 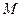может перейти в различные близкие состояния 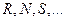, лежащие на этой прямой. Всем этим переходам соответствует одно и то же повышение температуры, но, вообще говоря, различные количества тепла 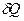. Будут разными и теплоёмкости системы при таких переходах.

Поэтому теплоёмкость есть характеристика не одного какого-либо состояния системы, а двух бесконечно близких состояний её, из которых одно является начальным, а другое конечным.

Вместо двух бесконечно близких состояний можно задать одно из них и направление пути перехода системы в бесконечно близкое состояние.

Таким образом, теплоёмкость не есть функция состояния тела, а является характеристикой бесконечно малого процесса, совершаемого телом.

Придадим этим рассуждениям количественную форму.

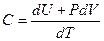
Так как

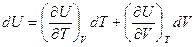
то

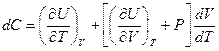
Объём 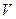зависит не только от температуры 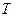, но и от даления 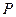. В зависимости от того как меняется давление, отношение 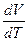может принять любое значение. Чтобы придать этому выражению однозначный смысл, надо фиксировать значение этого отношения. Иными словами, надо указать в плоскости 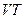направление пути, по которому система переходит в бесконечно близкое состояние.

Так как это направление может быть любым, то теплоёмкость 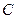, вообще говоря, может принимать любые значения от 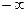до 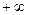. В частности:

для изотермического процесса 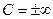, так как в этом случае .

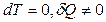для адиабатического процесса .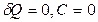

Особое значение имеют теплоёмкости при постоянном объёме (изохорная теплоёмкость 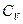) и постоянном давлении (изобарная теплоёмкость ).

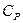Если объём остаётся постоянным, то 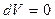, и следовательно,

.

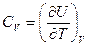Если процесс протекает при постоянном давлении, то на основании определения энтальпии 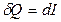. Поэтому

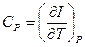
В фундаментальное уравнение термодинамики для закрытых систем 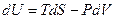входят пять переменных . Три величины можно измерить. Независимыми параметрами могут быть любые два из перечисленных пяти переменных, поэтому возможно записать целый ряд термодинамических функций состояния двух независимых переменных: 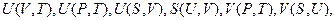и т.д.

Функция состояния системы двух независимых параметров называется характеристической, если посредством этой функции и её производных по этим параметрам могут быть выражены все термодинамические свойства системы.

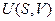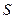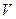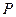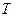Например, функция – характеристическая. и являются независимыми параметрами, а и определятся на основе уравнения (*).

,

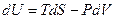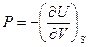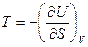
А величина энтальпии определится из соотношения

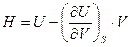
Можно легко убедиться, что такие функции, как 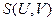и 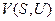также являются характеристическими. Можно записать ещё целый ряд характеристических функций, но обычно в термодинамике чаще всего используются четыре:

,

, (**)

,

.

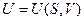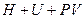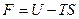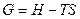Используя формулы (*) и (**) запишем дифференциалы этих функций и определим стандартные переменныесоответствующих характеристических функций:

Энтальпия Н.

,

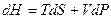Характеристическая функция .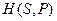

Свободная энергия Гельмгольца F.

.

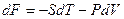Характеристическая функция .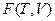

Свободная энергия Гиббса G.

.

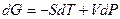Характеристическая функция .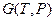

Функции 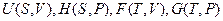называют также термодинамическими потенциалами. Дадим определение термодинамического потенциала.

Термодинамическим потенциалом называется характеристическая функция, убыль которой в обратимом процессе, идущем при постоянстве значений соответствующей пары параметров, равна максимальной полезной работе.

Термодинамические потенциалы стремятся к минимуму при движении системы к равновесию. Перепишем компактно выражения дифференциалов четырёх термодинамических потенциалов:

,

, (***)

,

.

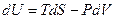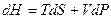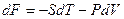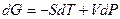Формулы (***) составляют основу для получения термодинамических соотношений, которые связывают термодинамические величины друг с другом и с экспериментально определяемыми параметрами. Такие соотношения можно получать различными способами. Например, имеется выражение для полного дифференциала вида

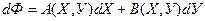
тогда справедливы следующие уравнения:

, ,

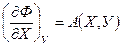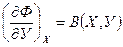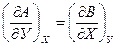
Используя () и () можно получить целый ряд полезных соотношений между термодинамическими величинами.

Энтропию обычно рассматривают как функцию переменных ; 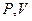или 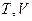. Записав выражение для полного дифференциала, находят соотношения между энтропией и экспериментально определяемыми параметрами системы.