Выбор оптимальных соотношений размеров многорамной стойки.
Одна из проблем, которые решаются при разработке конструкции ЭВМ, – сокращение потерь быстродействия из-за конечной скорости распространения сигналов по линиям межэлементных связей.
Общая задержка сигналов при преобразовании информации складывается из задержек сигналов tз.л.эв логических элементах и времени распространения сигналов tз.л.св линиях связи.
Длина линии связи между наиболее удаленными участками типовой конструкции зависит от ее компоновочной схемы. В связи с этим возникает задача выбора такой пространственной геометрии конструктивного модуля, которая при данном его объеме обеспечивала бы минимальную длину линии связи.
Последовательность решения задачи:1)выбрать критерий оптимизации;2)разработать модель;3)выявить влияющие факторы, т.е. варьируемые параметры;4)определить ограничения;5)найти зависимость целевой функции от варьируемых параметров;6)получить формальную постановку задачи;7)выбрать метод решения и реализовать его, выполняя необходимые преобразования.
Критерий – минимум длины линии связи между двумя наиболее удаленными точками конструктивного модуля.
Возможные методы решения:1)Поиск экстремумов функции.2)Использование методов теории геометрического программирования – совокупность методов решения комбинаторных задач непрерывной оптимизации.
Стандартная формулировка задачи геометрического программирования:
Найти 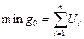 , при
, при 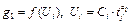 , где
, где 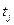 – варьируемые параметры,
– варьируемые параметры, 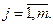
Ограничения: 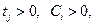
Ui– полином с положительными коэффициентами (позином);
ai,j– произвольные вещественные числа.
На основании теории двойственности минимум суммы g0сводится к максимуму двойственной функции v0.
Например при 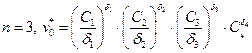 (1), где
(1), где 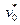 – оптимальное решение.
– оптимальное решение.
Далее составляется система:
| Для ортогональности: | Для нормализации: |
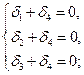
| 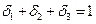
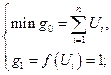
|
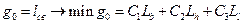 ;
; 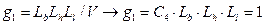
Отсюда следует, что 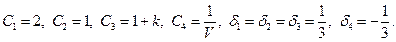
Подставим эти значения в (1) и получим: 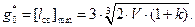
При этом 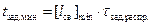
Оптимальное соотношение Lb, Lh, Llпозволяет найти следующее положение теории геометрического программирования: в точке оптимума целевой функции (ЦФ) коэффициенты diпоказывают вклад составляющих ЦФ в её оптимальное значение:
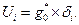 (2)
(2)
тогда 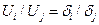 ;при
;при 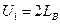 ;
; 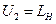 ;
; 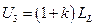 ,
,
имеем:
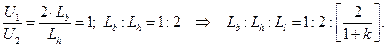
При известном значении 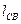 значение
значение 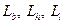 на основании (2) вычисляются как:
на основании (2) вычисляются как:
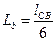 ,
, 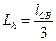 ,
, 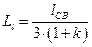
Дата добавления: 2016-07-18; просмотров: 1704;











