Электрический поверхностный эффект в плоской шине. Эффект близости

Рассмотрим явление поверхностного эффекта при прохождении переменного синусоидального тока частотой w вдоль пластины (шины) (рис. 5.7). Предположим, что обратная шина (обратный проводник) находится настолько далеко, что влиянием магнитного потока, вызванного током в ней, на распределение тока в исследуемой шине можно пренебречь.

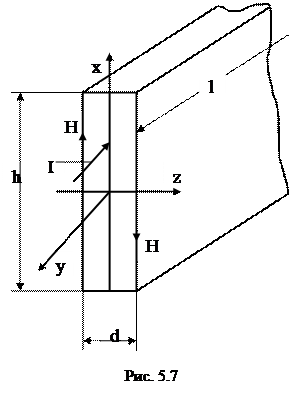
В этом случае поле внутри пластины определяется по формулам:

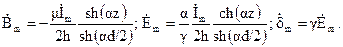
Сопротивление единицы длины шины

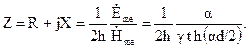(5.8)

Здесь 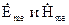- комплексные амплитуды напряженности электрического и магнитного поля на поверхности шины (z = d/2).

На рис. 5.8 приведены кривые B_m/B_me и E_m/E_me в функции от z для следующих параметров: m = 1000m₀; g = 10⁷ См/м; f = 500 Гц; d = 2 мм. Эти зависимости определяются формулами:

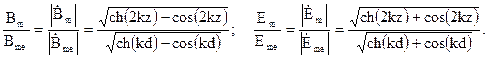
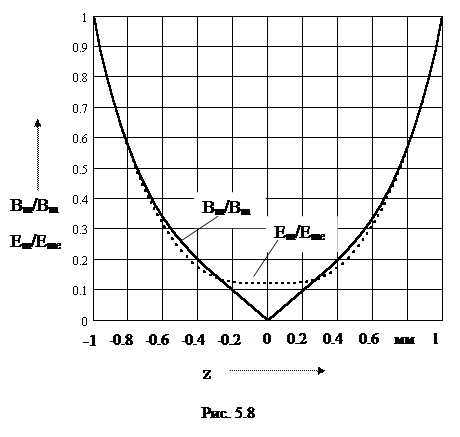
Как видно из рисунка, неравномерность распределения напряженности электрического поля (а значит, и плотности тока) довольно значительная. Так, напряженность поля в середине шины почти в десять раз меньше, чем на поверхности. В этом и заключается электрический поверхностный эффект.

Если в непосредственной близости друг от друга расположено несколько проводников с переменными токами и каждый из них находится не только в собственном переменном магнитном поле, но и в магнитном поле других проводников, то распределение в каждом проводнике будет несколько отличаться от того, которое имело бы место, если бы этот проводник был уединен. Этот эффект носит наименование эффекта близости. Он приводит к дополнительному увеличению активного сопротивления проводников.

В случае двухпроводной линии передачи, в проводах которой токи протекают в противоположных направлениях, эффект близости приводит к тому, что плотность тока на сторонах проводников, обращенных друг к другу, оказывается большей, чем на противоположных сторонах.

В качестве иллюстрации рассмотрим двухпроводную линию в виде двух параллельных близко расположенных плоских шин (рис. 5.9), по которым протекает в противоположных направлениях синусоидальный ток.

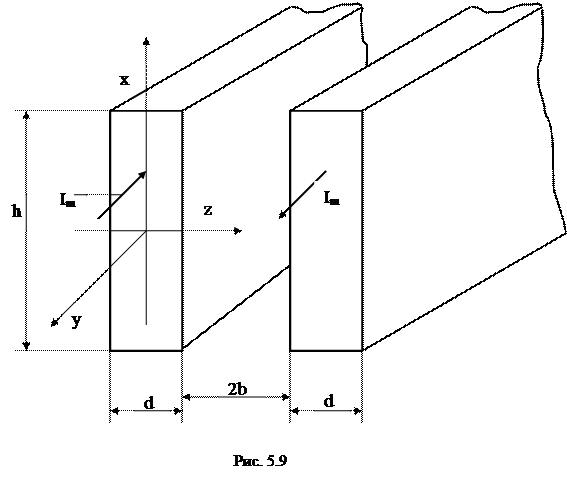
Поместим начало декартовой системы координат в средней плоскости левой шины и примем размеры d << h и 2b << h. В этом случае, с учетом того, что слева от левой шины напряженность магнитного поля Н = 0, а в пространстве между шинами Н = I/h (согласно закону полного тока), получим следующие формулы для определения Н и Е в левой шине:

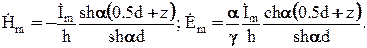
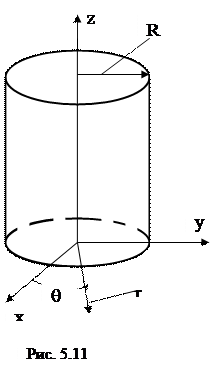
На рис. 5.10 приведены кривые Н_m/Н_me и E_m/E_me в функции от z для тех же параметров, что и в предыдущем примере. Здесь Н_me и E_me – значение наряженности магнитного и электрического поля на правой поверхности левой шины (z = 0.5d).

Как видно из рис. 5.10, в данном случае распределение напряженности электрического поля и напряженности магнитного поля (кривые практически совпадают) существенно отличаются от соответствующего распределения для одиночной шины (рис. 5.9).

Поверхностный эффект и эффект близости широко используют при поверхностной закалке стальных изделий индукционным методом. Так, если поднести плоский контур, по которому протекает ток высокой частоты, к плоской поверхности стального тела, то в этом теле вблизи его поверхности возникнут индуктированные токи. Эти токи и нагревают поверхностный слой тела напротив контура.