Поверхностный эффект в плоском ферромагнитном листе

Переменный электрический ток распределяется неравномерно по сечению проводов. На поверхности проводов плотность тока имеет наибольшее значение и убывает по мере удаления от поверхности. Это явление называется поверхностным эффектом.

Переменный магнитный поток в телах, обладающих конечной проводимостью, вызывает в этих телах вихревые токи, которые ослабляют магнитный поток внутри проводящего тела. Этот эффект иногда называют размагничивающим действием вихревых токов. По существу, и в этом случае мы имеем дело с явлением поверхностного эффекта.

Явление поверхностного эффекта можно объяснить, рассматривая проникновение электромагнитного поля вглубь проводящего тела.

Исследуем поле в стальном листе, вдоль которого проходит переменный синусоидальный поток Ф. Под действием этого потока (согласно закону электромагнитной индукции) индуктируются электродвижущие силы и возникают вихревые токи. Лист имеет толщину d, высоту h и длину l (рис. 5.5). Обычно длина и высота листа значительно превосходят его толщину (h >> d, l >> d). При этом можно пренебречь искривлением линий тока у краев листа и считать, что они направлены параллельно поверхности листа и перпендикулярно линиям магнитной индукции. При данных условиях электромагнитную волну можно считать плоской. Расположим оси координат декартовой системы так, как показано на рис. 5.5. Начало координат поместим в середине сечения листа. Сделаем допущение, что m = const. При этом для исследования поля можно использовать уравнения (5.2) и решение (5.3). Однако для определения постоянных интегрирования здесь необходимо поставить свои граничные условия. Так, поскольку электромагнитные волны проникают в лист с двух его сторон то на обеих поверхностях листа векторы магнитной индукции и напряженности магнитного поля должны быть одинаковыми. Это требование соблюдается при условии: А₁ = А₂ = А. Следовательно,

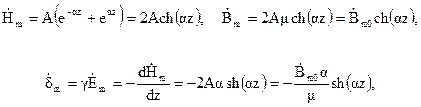
где 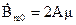представляет собой значение 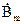в середине листа (z=0).

Отношение магнитной индукции в листе к магнитной индукции в средней плоскости листа:

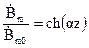
Левая и правая части последней формулы являются комплексами. Модуль ch(az) показывает во сколько раз модуль магнитной индукции в листе больше модуля магнитной индукции в середине листа. Найдем модуль ch(az).

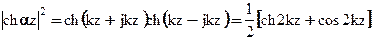
Таким образом,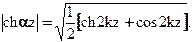

Следовательно,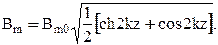

Аналогичным образом определяется величина амплитуды плотности тока:

,

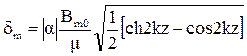здесь .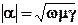

Рассмотрим числовой пример. Пусть m = 1000m₀; g = 10⁷ См/м; f =50 Гц; d = 0.5 мм. Параметр kd имеет при этом значение: 0.7.

На рис. 5.6 приведена кривая B_m/B_m0 в функции от 2kd. Из кривой видно, что при значении kd = 0.7 неравномерность распределения магнитного потока еще практически незаметна.

Однако при частоте f = 2000 Гц получаем kd = 4.4, и, соответственно, отношение амплитуды индукции на поверхности В_me к амплитуде индукции B_m0 в середине листа
оказывается равным В_me/ B_m0 = 4.5. Отсюда видно, что для звуковых частот толщина листа 0.5 мм очень велика. При звуковых частотах она должна быть порядка 0.05-0.1 мм. При радиочастотах уже и при таких малых толщинах листа поток распределяется весьма неравномерно по толщине листа – вихревые токи сильно ослабляют поле в середине листа. Поэтому при высоких частотах находят применение сердечники, спрессованные из тончайшего ферромагнитного порошка и изолирующего материала.

Отметим, что если вдоль листа направлен магнитный поток, то поверхностный эффект часто называют магнитным, а если вдоль плоской шины протекает переменный ток, то поверхностный эффект часто называют электрическим поверхностным эффектом, хотя природа их одна и та же. Таким образом, в данном разделе мы рассмотрели магнитный поверхностный эффект.