Передача с коническими колесами
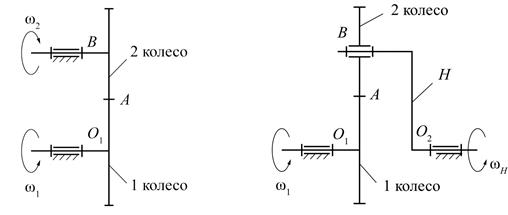
Пример 5. Определить передаточное отношение u 1Н (рис. 10),если числа зубьев колес равны z1 = 60; z2=40; z2’ = 20; z3 = 40
Запишем формулу Виллиса для центральных колес:
u 13(Н) = ( 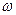 1 -
1 - 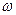 Н)/ (
Н)/ ( 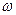 3 -
3 - 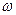 Н) =
Н) =
= - (z2 / z1)  (-z3 / z2’) = - 4/3
(-z3 / z2’) = - 4/3
где знак минус поставлен в соответствии с правилом стрелок (стрелки на первом и третьем колесах направлены противоположно). Делим числитель и знаменатель формулы Виллиса на минус  Н :
Н :
-u 1Н + 1 = u 13(Н) = -4/3;
u 1Н = 1+4/3 = 7/3
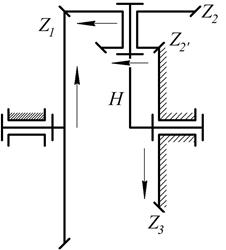
Рис.10. Передача с коническим приводом.
8.6. Метод планов линейных и угловых скоростей
Этот метод позволяет наглядно показать распределение скоростей звеньев непосредственно на схеме механизма, направление угловых скоростей, величину и знак передаточного отношения.
Пример 6.
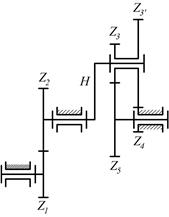
Рассмотрим схему дифференциального механизма (рис. 11).
Определим его подвижность:
W = n-рA=4-2 = 2
Пусть заданы угловые скорости первого колеса и водила. Схема механизма (рис.11-б)выполнена с масштабным коэффициентом L1 (м/мм)
Находим линейные скорости точек А и 02:
VА= r1 
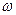 1 ; VО2 (r1 + r2)
1 ; VО2 (r1 + r2) 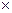
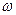 Н (6.1)
Н (6.1)
Изображаем скорость точки А отрезком (Аа). Тогда масштабный коэффициент скорости
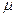 V = VА / (Аа) (м
V = VА / (Аа) (м 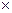 с-1 / мм )
с-1 / мм )
а) б) в)
 |
Рис. 11. Дифференциальный механизм.
а – торцевая плоскость; б – профильная плоскость; в – план угловых плоскостей.
Линейная скорость точки 02 изображается отрезком (О2 h) = VО2 /  V. Из точки В проводим горизонтальную линию, на которой расположена скорость VB, принадлежащая одновременно колесу 3 и сателлиту 2'. Соединяем точки а и h и, продолжая линию (ah) до пересечения с горизонтальной линией, получим точку b. Тогда скорость точки В равна VB = (Bb)
V. Из точки В проводим горизонтальную линию, на которой расположена скорость VB, принадлежащая одновременно колесу 3 и сателлиту 2'. Соединяем точки а и h и, продолжая линию (ah) до пересечения с горизонтальной линией, получим точку b. Тогда скорость точки В равна VB = (Bb) 
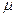 V
V
Угловая скорость колеса 3 равна
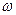 3 = VB / (r1 + r2 + r2’)
3 = VB / (r1 + r2 + r2’)
Угловая скорость сателлита находится из выражения:
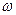 2 = u 21(Н)
2 = u 21(Н) 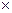
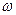 1 + (1- u 21(Н))
1 + (1- u 21(Н)) 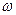 Н
Н
План угловых скоростей строится следующим образом. Из произвольной точки Р (рис.11-в)проводим линии (Р1), (РН), (Р3) параллельно отрезкам (о1а,), (o1,h), (o1,b). Из этой же точки откладываем вертикально произвольный отрезок (РК), через точку К проводим горизонтальную линию, которая ограничивает отрезки (Р1,), (РН), (Р3). Масштабный коэффициент угловых скоростей
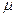 w =
w = 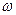 1 / (К1) (с-1 / мм)
1 / (К1) (с-1 / мм)
Отрезок (КН) = 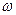 Н /
Н / 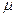 w . Угловая скорость
w . Угловая скорость 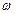 3 = (К3)
3 = (К3) 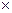
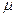 w
w
Найдем тангенсы углов J1, JH, J3 (рис.11-б):
tg 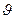 1 = (Аа)/(О1А) = (VА/
1 = (Аа)/(О1А) = (VА/ 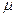 w )
w )  (
( 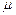 1 / r1) =
1 / r1) = 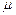 1 /
1 / 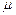 V
V 
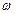 1
1
Аналогично
tg 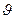 Н =
Н = 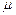 L /
L / 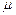 V
V 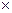
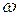 Н; tg
Н; tg 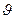 3 =
3 = 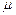 L /
L / 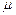 V
V 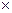
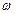 3;
3;
откуда 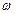 3 = (
3 = ( 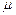 V /
V / 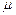 L )
L )  tg
tg 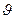 3 - искомая угловая скорость.
3 - искомая угловая скорость.
Проведенные построения показывают направление вращения каждого звена передачи и процесс суммирования скоростей, исходящих от звена 1 и водила Н на сателлите и центральном колесе 3.
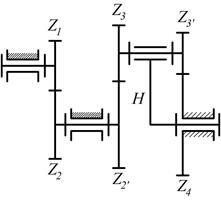
Пример 7. Рассмотрим более сложный случай построения плана угловых скоростей для конического планетарного редуктора (рис.12). Степень подвижности механизма:
W = n-р4 =4-3 = 1;
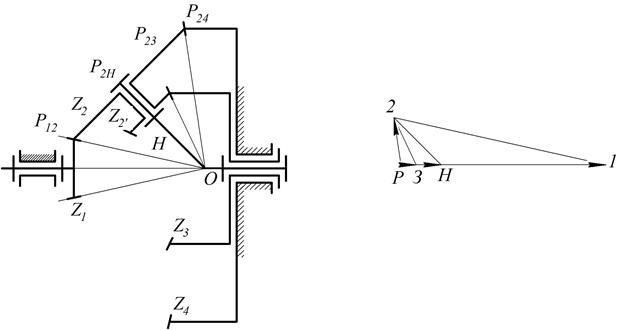 |
Рис. 12. Планетарный конический редуктор
Рис. 12. Планетарный конический редуктор
а – схема механизма;
б – план угловых скоростей.
Угловую скорость колеса 1 считают известной. Оси мгновенного относительного вращения обозначены Р120, Р2нО, Р230, Р240, они все пересекаются в точке О. Заметим, что ось Р240 является осью абсолютного движения, так как колесо 4неподвижно. Поэтому можно записать:
__ __ __ __ __ __
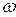 2 =
2 = 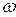 1 =
1 = 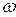 21 и
21 и 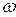 2 =
2 = 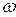 4 +
4 + 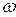 24 (6.2)
24 (6.2)
Из произвольной точки Р (рис. 12-6)откладываем отрезок (Р1), из точки 1 проводим линию, параллельную оси Р120. Так как 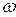 4 = 0, то из точки Р проводим линию, параллельную оси Р240. В пересечении этих линий получим точку 2. На основании уравнения
4 = 0, то из точки Р проводим линию, параллельную оси Р240. В пересечении этих линий получим точку 2. На основании уравнения
__ __ __
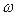 3 =
3 = 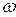 2 +
2 + 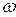 32 (6.3)
32 (6.3)
Из точки 2 проводим линию, параллельную оси Р230, до пересечения с горизонтальной линией в точке 3. Далее записываем уравнение
__ __ ___
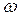 Н =
Н = 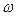 2 +
2 + 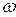 Н2 (6.4)
Н2 (6.4)
то есть через точку 2 надо провести линию, параллельную оси Р2НО. В результате получим точку Н.
Масштабный коэффициент плана угловых скоростей
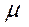
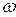 =
= 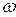 1 / (Р1) (с-1 / мм )
1 / (Р1) (с-1 / мм )
Угловые скорости остальных звеньев:
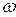 2 = (Р2)
2 = (Р2) 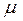
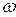 ;
; 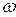 3 = (Р3)
3 = (Р3) 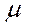
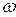 ;
; 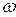 Н = (РН)
Н = (РН) 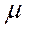
Из плана угловых скоростей хорошо видно направления относительных и абсолютных угловых скоростей, а также просто определяются их значения.
Задания на контрольную работу. Задачи.
 |
8.1. Определить числа оборотов водила и сателлита редуктора Давида, если число оборотов первого колеса n1=500 об/мин, а числа зубьев колес равны: z1=20; z2=40; z2*=20; z3=80; z4=60; z3*=60.
 |
8.2. Определить числа оборотов третьего колеса и сателлита редуктора Давида, если число оборотов первого колеса n1=540 об/мин, а числа зубьев колес равны: z=30; z2=50; z5*=72; z4=45; z3=24; z3*=75.
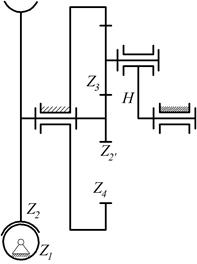 |
8.3. Определить числа оборотов водила и сателлита редуктора Джемса с приводом от червячной передачи, если числа зубьев колес равны: z1=l -число заходов червяка, z2=80 - число зубьев колеса, z2*=20; z3=30; z4=80. Число оборотов червяка n1=800 об/мин.
Примечание: передаточное отношение червячной передачи равно отношению числа зубьев колеса к числу заходов червяка.
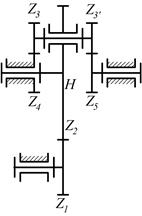 8.4. Определить числа
8.4. Определить числа
оборотов пятого колеса и сателлита планетарного редуктора, если n1=400 об/мин, а числа зубьев колес равны: z1=20; z2=80; z5=60; z3*=30; z=31;z4=60.
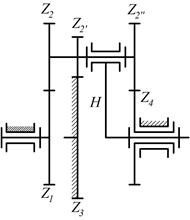 |
8.5. Найти числа оборотов водила, четвертого колеса и сателлита, если п=1500 об/мин, а числа зубьев колес равны: z1=28; z2=28; z2*=20; z2**=38; z3=36;z4=18.
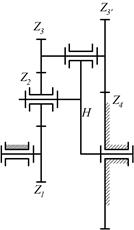 |
8.6. Найти числа оборотов водила и двух сателлитов, если число оборотов первого колеса n1 = 1000 об/мин, а числа зубьев колес равны: z1=30; z2=20; z3=20; z3* =30; z4=70.
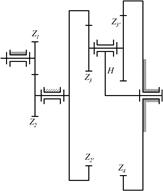 |
8.7. Определить числа оборотов водила и сателлита, если n1=750 об/мин, а числа зубьев колес равны: z,=20; z2=30; z2*=85; z3=40; z3*=58; z4=100.
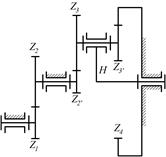 |
8.8. Определить числа оборотов водила и сателлита, если n1=750 об/мин, а числа зубьев колес равны: z1=20; z2=30; z2* = 18; z3=36 z3.=24; z4=85.
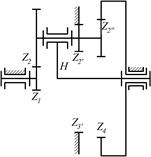 |
8.9. Определить числа оборотов водила, колеса 4 и сателлита, если n1=750 об/мин, а числа зубьев колес равны: z1=24; z2=36; z2*=20; z2**=40; z3=85; z4=104.
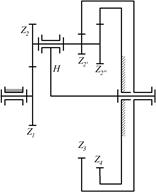 |
8.10. Определить числа оборотов водила, колеса 3 И сателлита, если n1=750 об/мин, а числа зубьев колес равны: z1=24; z2=36; z2*=20; z2** =40; z3=85; z4=104.
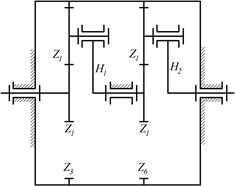 |
8.11. Найти числа оборотов водила Н2 и сателлитов, если n1=1240 об/ мин, а числа зубьев колес равны:z1=15; z2=75; z2*=165; z4=15; z5=75; z6=165
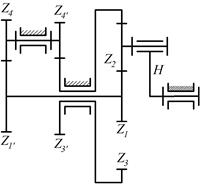 8.12. Найти числа оборотов всех колес, если число оборотов водила
8.12. Найти числа оборотов всех колес, если число оборотов водила  Н=750 об/мин, а числа зубьев колес равны: z1=26; z2=26; z3 =78; z3* =36; z4=18;z4*=34; z1*=20.
Н=750 об/мин, а числа зубьев колес равны: z1=26; z2=26; z3 =78; z3* =36; z4=18;z4*=34; z1*=20.
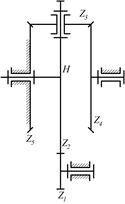 |
8.13. Определить передаточное отношение u|4 редуктора, если числа зубьев колес равны: z1=26; z2=130; z3=12; z4=54; z5=54.
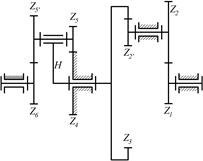 |
8.14. Определить передаточные отношения и16и ul5редуктора, если числа зубьев колес равны: z1 =15; z2*=15; z5=15; z3=75; z2=45; z4=45; z5* = 12; z6=48.
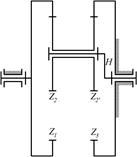 |
8.15.Определить передаточные отношения uH| и uH2 редуктора Давида, если числа зубьев колес равны: z1=65; z2=62; z2*=63; z3=66.
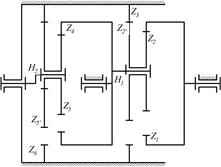 8.16.Определить передаточные отношения u1H2, u12, u15 редуктора Лопухова, если числа зубьев колес равны: z1=84; z2=80; z2*=82; z3=86; z4=84; z5 =80; z5* =82; z6=86.
8.16.Определить передаточные отношения u1H2, u12, u15 редуктора Лопухова, если числа зубьев колес равны: z1=84; z2=80; z2*=82; z3=86; z4=84; z5 =80; z5* =82; z6=86.
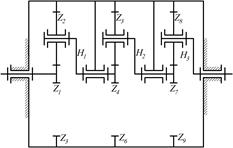 |
8.17. Определить числа оборотов звеньев Н1, Н2, Н3 и сателлитов, если n1=1500 об/мин, а числа зубьев колес равны: z1= z4= z7=15; z2=z5=z8=75;
z3= z6= z9=165
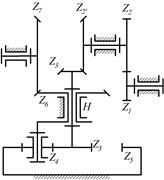 |
8.18. Определить числа оборотов всех колес, если число оборотов n1=1500 об/мин, а числа зубьев колес равны: z1= 18; z2=36; z2*=40; z3= 18; z3* =20; z4=30; z5=80; z6=65; z7=56.
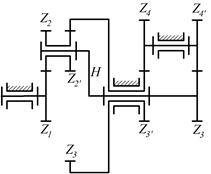 8.19. Определить числа оборотов всех колес, если число оборотов n1=750 об/мин, а числа зубьев колес равны: z1=45; z2 =46; z2*=22; z3=85; z3* =32; z4 =40; z4*=28; z5 =44.
8.19. Определить числа оборотов всех колес, если число оборотов n1=750 об/мин, а числа зубьев колес равны: z1=45; z2 =46; z2*=22; z3=85; z3* =32; z4 =40; z4*=28; z5 =44.
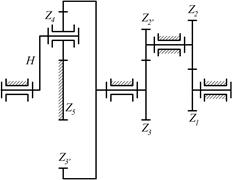 8.20. Определить числа оборотов всех колес и водила, если число оборотов n1 =1500 об/мин, а числа зубьев колес равны: z1=44; z2 =28; z2*=40; z3 =32; z3*=80; z4=30; z5 =20.
8.20. Определить числа оборотов всех колес и водила, если число оборотов n1 =1500 об/мин, а числа зубьев колес равны: z1=44; z2 =28; z2*=40; z3 =32; z3*=80; z4=30; z5 =20.
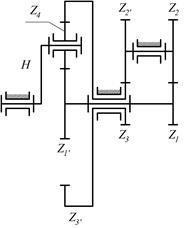 |
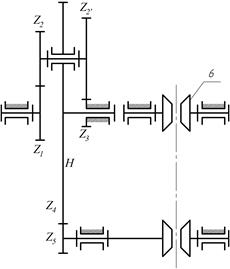
8.21. Определить числа оборотов всех колес, если число оборотов водила n1=750 об/мин, а числа зубьев колес равны: z1=44; z2=28; z2*=40; z3=32; z3*=80; z4=30; z1* =20.
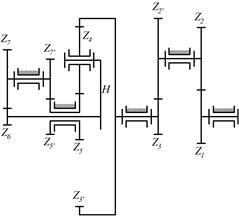 |
8.22. Определить числа оборотов всех колес, если число оборотов n1 =750 об/мин, а числа зубьев колес равны: z1=44; z2=28; z2* = 40; z3=32; z3* =80; z4 =30; z5=20; z5* = 15; z6=12; z7=31; z7*=28.
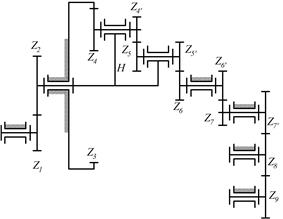 |
8.23. Определить числа оборотов всех колес, если число оборотов n1=1500 об/мин, а числа зубьев колес равны: z1 =20; z2=36; z3=85; z4=25; z4*=20; z5= 18; z5*=30; z6=24; z6*=32; г7=15; z8=15.
 |
8.24. Определить число оборотов ведомого вала 6 мультипликатора. Между валами 5 и 6 включен бесступенчатый клиноременный вариатор, мгновенное передаточное отношение которого зависит от расстояния обеих частей дисков вариатора. Дано: n1 =90 об/мин, z1=z2*=25; z2=z3=20; z4=100: z5=20; мгновенное передаточное отношение вариатора u65=4.
8.25. Определить числа оборотов всех звеньев, если n1=880 об/мин. а числа зубьеи колес равны: z1=24; z2=52; z2*= 21; z3=78; z3*=18; z4=78; z5=30.
8.26. Определить передаточное отношение редуктора Гуляева, если числа зубьев колес равны: z1=z3; z1*=101; z3 = 100; z4=99; z4* = 100. Рассмотреть два случая: а) входным звеном является колесо 1; б) входным звеном является колесо 4.. В обоих случаях выходным звеном является водило Н.
8.27. Найти передаточные отношения от первого колеса ко всем остальным звеньям, если числа зубьев колес равны: z1=30; z 2=20; z3=20; z3* =30; z4 =70; z4*=28; z5 =34; z6 =42; z6* =48.
8.28. Найти передаточные отношения от четвертого колеса ко всем остальным звеньям, если числа зубьев колес равны: z1=30; z2==20; z3=20; z3*=30; z4=70; z1*=40; z5=34; z5*=44; z6=30.
8.7 Специальные передаточные (планетарные) механизмы
Планетарным называется механизм, имеющий в своем составе хотя бы одно звено с подвижной геометрической осью в пространстве.
Звено, имеющее подвижную геометрическую ось в пространстве, называется сателлитом.
Звено, на которое устанавливают ось сателлитов, называется водилом (Н).
Зубчатые колеса, имеющие неподвижную геометрическую ось в пространстве, называются центральными.
Центральное колесо, имеющее внешние зубья, называется солнечным.
Центральное колесо, имеющее внутренние зубья, называется коронной шестерней (опорным колесом).
Достоинства планетарных передач:
1. Малые габариты и вес, обусловленные тем, что поток мощности, подводимый к центральному колесу, распределяется по k сателлитам (k – количество сателлитов). Затем поток мощности собирается на выходном звене. На одной планетарной передаче можно поставить до 24 сателлитов.
2. Очень высокий КПД, в среднем 0,99.
Недостаток планетарных передач – необходимость специального механизма (если число сателлитов не равно 3), который бы выравнивал нагрузку между сателлитами. Этот механизм утяжеляет и удорожает конструкцию.
8.8 Сравнительный анализ передачи
с неподвижными осями и планетарной передачи
Сравнительный анализ передачи с неподвижными осями и планетарной передачи представлен на рис. 8.1.
Через число зубьев 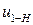 записать нельзя, т.к. ось В – подвижная ось.
записать нельзя, т.к. ось В – подвижная ось.
Чтобы записать передаточное отношение через число зубьев, применим метод обращения движения, т.е. мысленно сообщим всем звеньям
а б
Рис. 8.1. Сравнительный анализ зубчатых передач:
а – ось В неподвижна; б – ось В подвижна
механизма, включая стойку, дополнительное движение с угловой скоростью 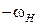 . Получим обращенный планетарный механизм с неподвижными осями зубчатых колес.
. Получим обращенный планетарный механизм с неподвижными осями зубчатых колес.
В обращенном движении звенья этого механизма будут иметь следующие угловые скорости:
 = w1 – wН,
= w1 – wН,
 = w2 + (– wН) = w2 – wН,
= w2 + (– wН) = w2 – wН,
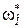 = wН – wН = 0,
= wН – wН = 0,
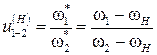 (формула Виллиса).
(формула Виллиса).
8.9 Определение передаточного отношения планетарных
механизмов различных схем
Передаточное отношение можно определить:
1. Графическим способом по чертежу.
2. Аналитическим способом, используя формулу Виллиса.
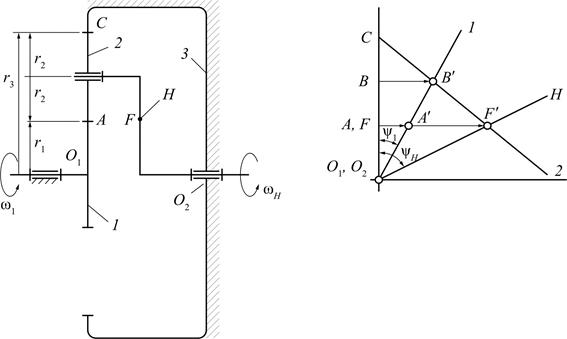
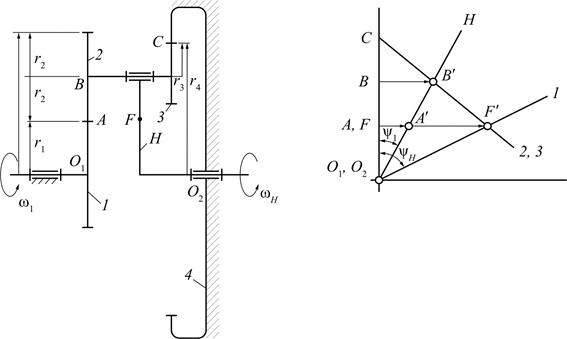
Планетарный однорядный механизм (механизм Джеймса)и графический способ определения передаточного отношения представлены на рис. 8.2.
а б
Рис. 8.2. Планетарный зубчатый механизм (механизм Джеймса):
а – схема механизма; б – графический способ определения
передаточного отношения
Выберем на водиле Н точку F, которая расположена на том же расстоянии от оси О2, что и точка А.
Оси О1 и О2 расположены на одном уровне.
Для данной схемы входное звено – звено 1 (солнечное колесо), выходным является водило Н.
Зададимся отрезком 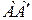 , который изображает линейную скорость колеса 1 в точке А. Так как колесо 1 вращается вокруг О1, то закон распределения линейной скорости по первому звену изображается прямой линией О1А′. Сателлит 2 в т. А имеет такую же линейную скорость, что и колесо 1. В т. С сателлит 2 имеет мгновенный центр скоростей (МЦС) в абсолютном движении, т.к. идет контакт с неподвижным колесом 3. Закон распределения линейной скорости по второму колесу изображается прямой линией СА′. В т. В сателлит имеет линейную скорость, которая изображается отрезком ВВ′, однако т. В является также и осью водила Н, которое вращается вокруг О2. Следовательно, закон распределения линейной скорости по водилу изобразится прямой линией О2В′. Для точки F водила линейная скорость изображается отрезком FF′.
, который изображает линейную скорость колеса 1 в точке А. Так как колесо 1 вращается вокруг О1, то закон распределения линейной скорости по первому звену изображается прямой линией О1А′. Сателлит 2 в т. А имеет такую же линейную скорость, что и колесо 1. В т. С сателлит 2 имеет мгновенный центр скоростей (МЦС) в абсолютном движении, т.к. идет контакт с неподвижным колесом 3. Закон распределения линейной скорости по второму колесу изображается прямой линией СА′. В т. В сателлит имеет линейную скорость, которая изображается отрезком ВВ′, однако т. В является также и осью водила Н, которое вращается вокруг О2. Следовательно, закон распределения линейной скорости по водилу изобразится прямой линией О2В′. Для точки F водила линейная скорость изображается отрезком FF′.
От вертикали до линии распределения скоростей по водилу измеряем угол ψH, а от вертикали до линии распределения скоростей по колесу 1 – угол ψ1. Так как углы ψ1 и ψH отложены от вертикали в одном направлении, то это показывает, что входное звено 1 и выходное звено вращаются в одном направлении.
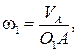
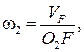
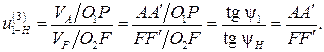
Определим передаточное отношение аналитическим способом. Применим метод инверсии движения, обратив планетарный механизм в непланетарный.
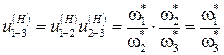 ,
,
где 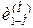 – передаточное отношение от 1-го зубчатого колеса к 3-му при фиксированном поводке.
– передаточное отношение от 1-го зубчатого колеса к 3-му при фиксированном поводке.
w1* = w1 – wН,
w3* = w3 – wН,
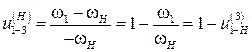 ,
,
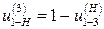 ,
,
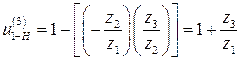 (плюсовой механизм),
(плюсовой механизм),
¨ где  – число зубьев зубчатых колес.
– число зубьев зубчатых колес.
Планетарный механизм со смешанным зацеплением (с одним внешним и одним внутренним зацеплением) показан на рис. 8.3, где
1 – солнечное колесо; 2, 3 – блок сателлитов; 4 – коронная шестерня; Н – водило.
Выберем на выходном звене (на водиле) точку F так, чтобы O1A = O2F (O1 и O2 соосны).
а б
Рис. 8.3. Планетарный механизм со смешанным зацеплением колес:
а – схема механизма; б – графический метод определения
передаточного отношения
Определим передаточное отношение графическим способом:
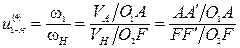 ,
,
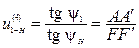 .
.
Отрезок АА′ выбирается произвольно.
Теперь определим передаточное отношение аналитическим способом.
Обратим мысленно планетарный механизм в механизм с неподвижным водилом, для того чтобы использовать формулы для механизма с неподвижными осями зубчатых колес (применим метод обращения движения).
В обращенном движении угловая скорость
1-го звена: 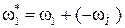 ,
,
2-го звена: 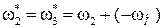 ,
,
3-го звена: 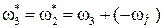 ,
,
4-го звена: 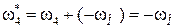 ,
,
5-го звена: 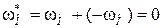 .
.
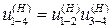 ,
,
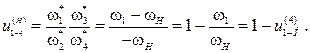
Если переписать последнее уравнение, учитывая количество зубьев, то получим
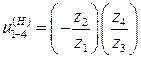 ,
,
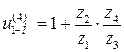 .
.
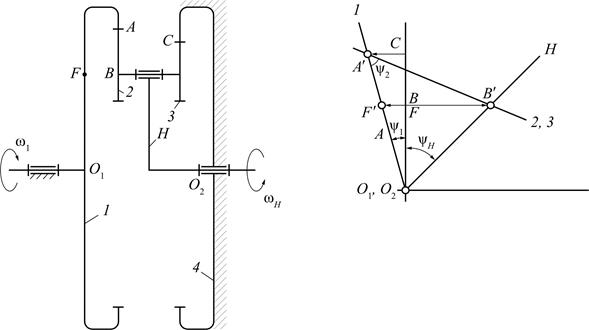
Механизм с двумя внутренними зацеплениями представлен на рис. 8.4.
а б
Рис. 8.4. Планетарный механизм с внутренними зацеплениями:
а – схема механизма; б – графический метод определения
передаточного отношения
Тогда при η = 0,99 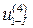 = 20…50. Входное звено – водило, выходное – первое колесо.
= 20…50. Входное звено – водило, выходное – первое колесо.
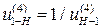 .
.
Например, если 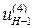 = 20, то
= 20, то 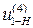 = 1 /20.
= 1 /20.
Используем графический способ.
Выберем точку F на входном звене так, чтобы O1F = O2B.
Точка С для данной схемы может располагаться как выше, так и ниже точки А. В зависимости от положения точки С план скоростей будет разный.
ψ1 и ψН направлены в разные стороны от вертикали. Следовательно, водило и колесо 1 вращаются в разные стороны.
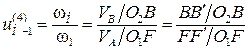 ,
,
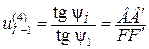 .
.
Определим передаточное отношение аналитическим способом.
Применим метод обращения движения.
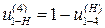 .
.
Запишем передаточное отношение через число зубьев:
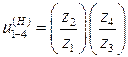 ,
,
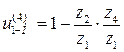 .
.
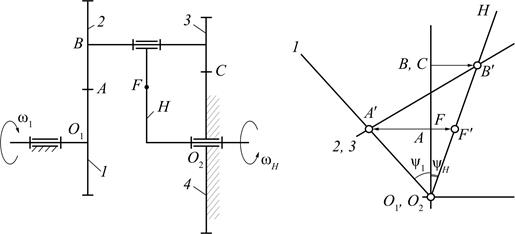
Планетарный механизм с двумя внешними зацеплениями (механизм Давида) представлен на рис. 8.5.
Механизм Давида применяется в приборных устройствах, так как 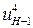 достигает 10 000. Его недостаток – низкий КПД.
достигает 10 000. Его недостаток – низкий КПД.
Определим передаточное отношение графическим способом.
Выберем на водиле Н точку F так, чтобы O2F = O1A (валы O1 и O2 соосны). Точка С может быть выше или ниже точки А. FF′ – произвольный отрезок (линейная скорость точки F). Для колес 2 и 3 точка С – мгновенный центр скоростей.
а б
Рис. 8.5. Планетарный механизм с двумя внешними зацеплениями:
а – схема механизма; б – графический метод определения
передаточного отношения
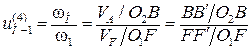 ,
,
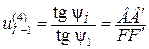 .
.
Запишем результаты определения передаточного отношения аналитическим способом.
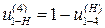 ,
,
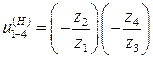 ,
,
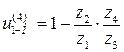 .
.
Дата добавления: 2020-07-18; просмотров: 841;











