Результативности торговли

Для каждой сложной проблемы существует простое, изящное и неверное решение

X./I. Менкен

НЕОБХОДИМОСТЬ НОРМАЛИЗАЦИИ ПРИБЫЛИ*

Слишком многие инвесторы при оценке финансовых управляющих со­вершают ошибку, фокусируясь исключительно на доходности**.

Помимо доходности, совершенно необходимо встраивать в процесс оценки некоторый способ измерения риска. Рассмотрим колебания сто­имости активов на счетах менеджеров А и В на рис. 21.1***.

Хотя доходность менеджера А выше, если рассматривать весь пе­риод как целое, вряд ли можно утверждать, что А торгует лучше, чем В — обратите внимание на большое количество резких падений сто­имости активов.

Следующий раздел представляет собой адаптацию статьи Дж. Швагера «Alternative to Sharpe Ratio Better Measure of Performance», Futures, p. 56-57, March 1985.

Большинство финансовых управляющих, работающих в сфере торговли фьючерсами (зарегистрированных Комиссией по торговле товарными фьючер­сами), называются «советниками по фьючерсной торговле» (commodity trading advisors — СТА). Название, по моему мнению, на редкость неудачное. В этой главе используется более общий термин «финансовый управляющий», который можно рассматривать как взаимозаменяемый с СТА.

Хотя в примерах из этой главы оценивается результативность финансовых управляющих, похожие примеры могли бы быть приведены и в случае торго­вых систем. Там, где это необходимо, в явном виде указано на различия в спо­собах оценки результативности финансового управляющего и системы.

734 ЧАСТЬ 4. торговые системы и измерение эффективности торговли

Рисунок 21.1. НЕОБХОДИМОСТЬ НОРМАЛИЗАЦИИ ПРИБЫЛИ

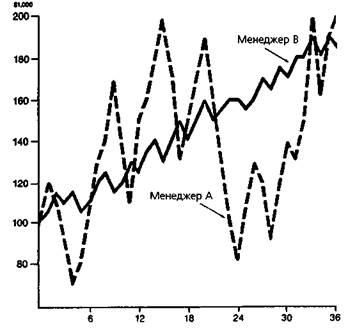
Источник: Дж. Швагер «Alternative to Sharpe Ratio Better Measure of Performance», Futures, p. 56, March 1985.

И эта черта является негативной не просто потому, что инвесторы, работающие с менеджером А, будут переживать много неприятных пе­риодов. Ещё более важно то обстоятельство, что инвесторы, начинаю­щие работать с менеджером А в плохой момент (а это вполне возмож­но), могут понести существенные убытки. Предполагая, что счет закры­вается, когда потеряны 25-50% начальных активов, есть большая ве­роятность того, что инвесторы, работающие с менеджером А, будут вы­биты из игры раньше, чем начнется период высокой результативности.

Кажется разумным предположить, что большинство инвесторов предпочли бы менеджера В менеджеру А, поскольку немного более низкая доходность менеджера В с лихвой компенсируется значительно меньшим риском. Более того, если бы менеджер В использовал немно­го более высокое соотношение «маржа/активы» (маржинальное плечо), его доходность оказалась бы лучше, чем у менеджера А, а падения сто­имости активов по-прежнему были бы сравнительно небольшими. (Ис-

ГЛАВА 21. измерение результативности торговли 735

ходя из требований управления капиталом все управляющие будут ог­раничивать размер открытых позиций таким образом, чтобы отношение «маржа/размер открытых позиций» было равным 0,15-0,35.)

Ясно, что менеджер В имеет лучшую историю деятельности. Как показано на этом примере, любой разумный метод оценки результатив­ности должен включать в себя способ измерения риска.

КОЭФФИЦИЕНТ ШАРПА

Необходимость рассматривать риск при оценке результативности была понята давно. Классическая мера отношения прибыльности к риско­ванности — коэффициент Шарпа — может быть выражена следующим образом:

E-I

SR =

где £ — ожидаемая доходность,

/ — безрисковая процентная ставка, sd — стандартное отклонение прибыли.

£ обычно выражается как процентная доходность. Как правило, ожидаемая доходность предполагается равной средней доходности в прошлом. Поэтому, несмотря на то что £ всегда обозначает ожидаемую будущую доходность, мы будем использовать ее как синоним средней доходности в прошлом.

Введение / в коэффициент Шарпа раскрывает, что инвестор все­гда мог бы заработать определенную безрисковую прибыль — напри­мер, инвестируя в казначейские векселя. Таким образом, доходность, превышающая безрисковую ставку, более значима, чем абсолютный уровень доходности.

Стандартное отклонение — это статистическая величина, предназ­наченная для измерения степени разброса данных. Формула для стан­дартного отклонения такова:

sd =

1=1

N-l

где X— среднее значение,

X. — отдельные значения данных, N — количество сегментов данных.

736 ЧАСТЬ 4. торговые системы и измерение эффективности торговли

В применении к коэффициенту Шарпа N равно количеству времен­ных интервалов. Например, если для исследуемого трехгодичного пе­риода используются месячные временные интервалы, то N = 36.

При вычислении стандартного отклонения всегда необходимо вы­бирать временной интервал для сегментирования всего рассматрива­емого периода имеющихся данных (недельные или месячные интерва­лы). Пусть, к примеру, данные о доходности финансового управляю­щего за данный год разбиты на недельные сегменты. Стандартное от­клонение будет очень высоким, если доходность некоторых недель рез­ко отличается от средней доходности за весь период имеющихся дан­ных. И наоборот, стандартное отклонение будет низким, если доход­ности отдельных недель располагаются близко к средней доходности. Рис. 21.2 иллюстрирует два набора данных с одной и той же средней недельной доходностью, но существенно различными стандартными от­клонениями.

Базовая предпосылка коэффициента Шарпа состоит в том, что стан­дартное отклонение измеряет риск. То есть чем больше отклонение доходности отдельных сегментов от среднего значения доходности, тем более рискованны инвестиции. В сущности, стандартное отклонение измеряет неопределенность прибыли. Должно быть интуитивно понят­но, что при небольшом стандартном отклонении реальная прибыль ско­рее всего будет близка к ожидаемой (если, конечно, ожидаемая при­быль является хорошей оценкой реальной прибыли). С другой сторо­ны, если стандартное отклонение велико, то оно предполагает большую вероятность того, что реальная прибыль будет существенно отличаться от ожидаемой.

Коэффициент Шарпа для финансового управляющего может быть вычислен напрямую, поскольку мы знаем величину активов, по отноше­нию к которым вычисляется доходность. В случае торговой системы это не так. Применяя коэффициент Шарпа к торговой системе, мы можем выбрать один из двух подходов:

1. Оценить активы, которые требуются, чтобы торговать с помо­
щью системы, и использовать эту оценку для вычисления про­
центной доходности.

2. Упростить коэффициент Шарпа, удалив из него безрисковую
процентную ставку /. (Как объясняется далее, если использует­
ся такая форма коэффициента Шарпа, то нет необходимости
оценивать активы, требующиеся для торговли с помощью сис­
темы.) Таким образом, коэффициент Шарпа сократится до

SR = E/scf.

ГЛАВА 21. измерение результативности торговли 737

Рисунок 21.2.