Структурные средние величины (мода, медиана)

К структурным средним величинам относят моду и медиану.

Мода – чаще всего встречающаяся варианта в ряду распределения. Она представляет собой типичное значение признака.

В зависимости от вида ряда распределения мода определяется по-разному.

1). В ранжированном ряду мода – это варианта, которая повторяется наибольшее количество раз.

2). В дискретном ряду мода – это варианта с наибольшей частотой.

3). В интервальном ряду мода – это центральная варианта модального интервала, т.е. того интервала, который имеет наибольшую частоту. Такой расчет будет верным, если сохраняется полная симметричность ряда распределения, т.е. одинакова разность значений в пределах каждого интервала и между интервалами.

,

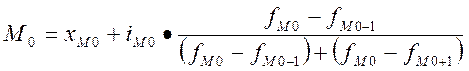где x_М0 – нижняя граница модального интервала,

i_М0 - величина модального интервала,

f_М0 - частота модального интервала,

f_М0-1 – частота интервала, предыдущего модальному,

f_М0+1 – частота интервала, следующего за модальным.

Средняя величина является обобщающей характеристикой совокупности, но в ряде случаев мода наиболее эффективна.

Пример: при оценке качества передачи информации целесообразнее рассчитывать моду. Так, для телеграфной связи один из показателей качества – это процент телеграмм, преданных в контрольные сроки. По разным причинам он может колебаться в пределах от 0 до 100 %, но для большинства предприятий характерен показатель, близкий к 100%, т.е. мода, а не обычная средняя величина.

Графически мода может быть определена по гистограмме.

Медиана – это варианта, которая делит численность ряда распределения пополам, при этом варианты, сосредоточенные в первой половине, имеют значения меньше, чем медиана, а в другой половине - больше медианы.

1) в ранжированном ряду: с нечетным количеством вариант медиана – это центральная варианта, с четным количеством вариант медиана – это результат от деления на 2 суммы смежных центральных вариант;

2) в дискретном ряду, для того чтобы найти медиану, определяют сумму накопленных частот, ее делят на 2 и результат показывает, на каком месте от начала или конца ряда находится медиана;

3) в интервальном ряду распределения:

- определяем сумму накопленных частот.

- по данным о накопленных частотах определяем медианный интервал

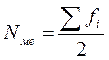
- рассчитываем медиану в найденном интервале

,

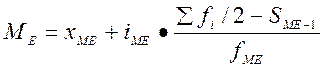где x_МЕ – нижняя граница медианного интервала,

i_МЕ - величина медианного интервала,

åf_i/2 - полусумма частот ряда,

S_МЕ-1 – сумма накопленных частот до медианного интервала,

F_МЕ – частота медианного интервала.

Графически медиану определяют по кумуляте.