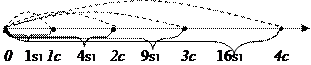Для частных случаев решения задач.
1. Разложение вектора на проекции.
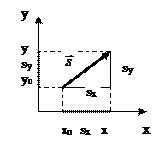 Модуль вектора может быть найден по теореме Пифагора:
S =
Модуль вектора может быть найден по теореме Пифагора:
S = 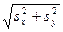 
| 2 . Средняя скорость.
1) по определению 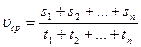 2)
2) 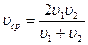 для 2х S; если
3) для 2х S; если
3) 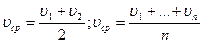 , ,
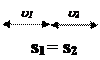 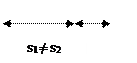 если t1 = t2 = … = tn u1 u2 если t1 = t2 = … = tn u1 u2
| ||||||
3. Метод площадей.
На графике uх(t) площадь фигуры
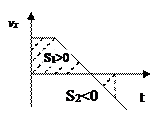 численно равна перемещению или пройденному пути.
S =S1 - S2
ℓ = S1+ S2 численно равна перемещению или пройденному пути.
S =S1 - S2
ℓ = S1+ S2
| 4. Физический смысл производной.
Для уравнений координаты х(t) и y(t) →
ux = x΄, uy = y΄, и
ах = u΄x = x΄΄, аy = u΄y = y΄΄,
 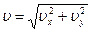
 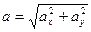
| ||||||
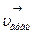 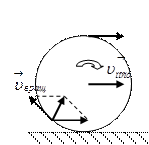 5. Движение колеса без проскальзывания.
uпост = u вращ 5. Движение колеса без проскальзывания.
uпост = u вращ
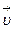 (если нет проскальзывания) (если нет проскальзывания)
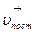 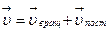 Скорость точки на ободе колеса относительно земли.
Скорость точки на ободе колеса относительно земли.
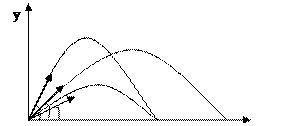
| 6. Дальность полёта.
Дальность полета максимальна при угле бросания 45˚ υ0 = const
| ||||||
7. Свойства перемещения для равноускоренного движения при uo=0.
S1 за t =1с S1= 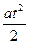 = = 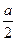 Отношение перемещений сделанных за одну секунду, при uo=0 равно:
Отношение перемещений сделанных за одну секунду, при uo=0 равно:
 1) 1)
S1: S2: S3: …: Sn = 1: 3: 5: 7: ….: (2n-1) Sn = S1(2n – 1) = | 2) Отношение перемещений сделанных за время от начала отсчета, при uo=0 равно:
S1: S2: S3: …: Sn = 12: 22: 32: 42: ….: n2 Sn = S1n2 = |
Обучающие задания.
1(А) Решаются две задачи:
а) рассчитывается маневр стыковки двух космических кораблей;
б) рассчитывается период обращения космических кораблей вокруг Земли.
В каком случае космические корабли можно рассматривать как материальные точки?
1) Только в первом случае.
2) Только во втором случае.
3) В обоих случаях.
4) Ни в первом, ни во втором случае.
2(А)Колесоскатывается с ровной горки по прямой линии. Какую траекторию описывает точка на ободе колеса относительно поверхности дороги?
1) Окружность. 3) Спираль.
2) Циклоиду. 4) Прямую.
3(А)Чему равно перемещение точки движущейся по окружности радиусом R при его повороте на 60º?
1) R/2 2) R 3) 2R 4) R 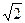
Указание: постройте чертеж, отметьте два положения тела, перемещение будет хордой, проанализируйте каким получится треугольник (все углы по 60º).
4(A) Какой путь проделает катер, делая полный разворот радиусом 2м?
1) 2 м 3) 6,28 м
2) 4 м 4) 12,56 м
Указание: сделайте чертеж, путь здесь это длина полуокружности.
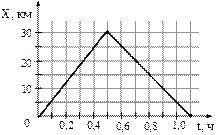 5(А)На рисунке представлен график движения автобуса из пункта А в пункт Б и обратно. Пункт А находится в точке х = 0, а пункт Б – в точке х = 30 км. Чему равна максимальная путевая скорость автобуса на всем пути следования туда и обратно?
5(А)На рисунке представлен график движения автобуса из пункта А в пункт Б и обратно. Пункт А находится в точке х = 0, а пункт Б – в точке х = 30 км. Чему равна максимальная путевая скорость автобуса на всем пути следования туда и обратно?
1) 40 км/ч
2) 50 км/ч
3) 60 км/ ч
4) 75 км/ч
6(А) Тело начинает движение прямолинейно равноускоренно вдоль оси Ох. Укажите правильное расположение векторов скорости, и ускорения в момент времени t.
|
|

 1) х 3) х
1) х 3) х
 |  |  |  |
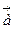
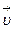
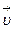
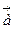
2) х 4) х
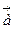
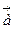
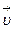
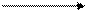
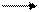
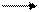
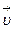
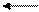
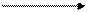
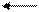
Указание: при прямолинейном движении векторы v и а направлены вдоль одной прямой, при увеличении скорости – сонаправлены.
7(А)Автомобиль половину пути проходит со скоростью u1, а вторую половину пути со скоростью u2, двигаясь в том же направлении. Чему равна средняя скорость автомобиля?
1) 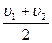 3)
3) 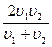
2) 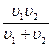 4)
4) 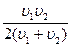
Указание: данная задача является частным случаем нахождения средней скорости. Вывод формулы исходит из определения
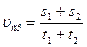 , где s1=s2, а t1 =
, где s1=s2, а t1 = 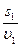 и t2=
и t2= 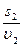
8(А)Уравнение зависимости проекции скорости движущегося тела от времени имеет вид: ux= 3-2t(м/с).Каково уравнение проекции перемещения тела?
1) sx=2t2 (м) 3) sx=2t-3t2 (м)
2) sx=3t-2t2 (м) 4) sx=3t-t2 (м)
Указание: запишите уравнение скорости равноускоренного движения в общем виде и, сравнив его с данным в задаче, найдите чему равны u0 и а, вставьте эти данные в уравнение перемещения, записанное в общем виде.
9(А)Какой путь пройдет свободно падающее из состояния покоя тело за пятую секунду? Ускорение свободного падения принять за 10м/с2.
1) 45 м 2) 55 м 3) 125 м 4) 250 м
Указание: запишите выражение h для случая uo =0, искомое h= h5- h4, где соответственно h за 5 с и 4 с.
10(А) Если тело, начавшее двигаться равноускоренно из состояния покоя, за первую секунду проходит путь S, то за первые три секунды оно пройдет путь
1) 3S 2) 4S 3) 8S 4) 9S
Указание: используйте свойства перемещения равноускоренного движения для u0=0
11(А)Два автомобиля движутся на встречу друг другу со скоростями 20 м/с и 90 км/ч, соответственно. Какова по модулю скорость первого относительно второго?
1) 110 м/с 2) 60 м/с 3) 45 м/с 4) 5м/с
Указание: Относительная скорость - это разность векторов, т.к. векторы скоростей направлены противоположно, она равна сумме их модулей.
12(А) Наблюдатель с берега видит, что пловец пересекает реку шириной h=189 м перпендикулярно берегу. При этом скорость течения реки u=1,2 м/с, а скорость пловца относительно воды u=1,5м/с. Пловец пересечет реку за ….
1) 70 с 2) 98 с 3) 126 с 4) 210 с
Указание: постройте треугольник скоростей исходя из 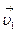 =
= 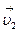 +
+ 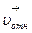 , перейдите к теореме Пифагора, выразите из неё скорость пловца относительно берега, и с ней найдите время.
, перейдите к теореме Пифагора, выразите из неё скорость пловца относительно берега, и с ней найдите время.
13(А)Прискорости 10 м/с время торможения грузового автомобиля равно 3с. Если при торможении ускорение автомобиля постоянно и не зависит от начальной скорости, то при торможении автомобиль снизит свою скорость от 16м/с до 9 м/с за …
1) 1,5 с 2) 2,1 с 3) 3,5 с 4) 4,5 с
Указание: из рассмотрения первой ситуации найдите ускорение и подставьте его в уравнение скорости для второй ситуации, из него и можно выразить искомое время.
14(А) От пристани отходит теплоход, движущийся с постоянной скоростью 18км/ч, через 40 с от той же пристани вдогонку отправляется катер с ускорением 0,5 м/с2. Через какое время он догонит теплоход, двигаясь с постоянным ускорением?
1) 20 с 2) 30 с 3) 40 с 4) 50 с
Указание: примите время движения катера за t, тогда время движения теплохода t+40, запишите выражения перемещения теплохода (движение равномерное) и катера (движение равноускоренное) и приравняйте их. Решите квадратное получившееся квадратное уравнение относительно t. Не забудьте сделать перевод единиц 18 км/ч = 5 м/с.
15(А) Двое играют в мяч, бросая его под углом α=60º к горизонту. Мяч находится в полете t =2 с. При этом расстояние, на котором находятся играющие, равно
1) 9,5 м 2) 10 м 3) 10,5 м 4) 11,5 м
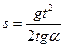 Указание: сделайте рисунок – в осях х,у – траектория парабола, точка пересечения параболы с осью х соответствует дальности полета, в этой точке уравнение x(t) имеет вид s=uocos60ºt. Для нахождения u0 используйте уравнение y(t), которое в той же точке имеет вид 0=uosin60ºt-
Указание: сделайте рисунок – в осях х,у – траектория парабола, точка пересечения параболы с осью х соответствует дальности полета, в этой точке уравнение x(t) имеет вид s=uocos60ºt. Для нахождения u0 используйте уравнение y(t), которое в той же точке имеет вид 0=uosin60ºt- 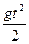 . Из этого уравнения выразить uo и подставить в первое уравнение. Расчетная формула имеет вид
. Из этого уравнения выразить uo и подставить в первое уравнение. Расчетная формула имеет вид 
16(А)Самолет летит с грузом к месту назначения на высоте 405м над песчаной местностью с горизонтальным профилем со скоростью 130 м/с. Чтобы груз попал в намеченное место на земле (силой сопротивления движения пренебречь), летчик должен освободить его от крепежа, не долетев до цели
1) 0,53 км 3) 0,95 км
2) 0,81 км 4) 1,17 км
Указание: рассмотрите в теории пример «Движение тела брошенного горизонтально». Из выражения высоты полета выразите время падения и подставьте его в формулу дальности полета.
17(В)Материальная точка движется с постоянной скоростью по окружности радиуса R, совершая один оборот за время Т. Как изменятся перечисленные в первом столбце физические величины, если радиус окружности увеличится, а период обращения останется прежним
Физические величины. Их изменение.
А) Скорость 1) увеличится
Б) Угловая скорость 2)уменьшится
В) Центростремительное 3)не изменится
ускорение
| А | Б | В |
Указание: запишите определяющие формулы предложенных величин через R и проанализируйте их математическую зависимость с учетом постоянства периода, Цифры правого столбца могут повторяться.
18(В)Чему равна линейная скорость точки поверхности земного шара, соответствующей 60º северной широты? Радиус Земли 6400 км. Ответ дать в м/с, округлить до целых.
Указание: сделайте чертеж и обратите внимание, что точка на указанной широте вращается относительно земной оси по окружности с радиусом r = Rземcos60º.
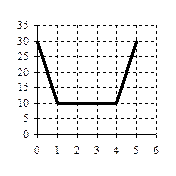
 19(В)По графику зависимости скорости тела от времени определить путь, пройденный за 5 с. υ, м/с
19(В)По графику зависимости скорости тела от времени определить путь, пройденный за 5 с. υ, м/с
T, с

Указание: наиболее простой способ нахождения пути через площадь фигуры под графиком. Сложную фигуру можно представить как сумму двух трапеций и одного прямоугольника.
20(С) Наклонная плоскость пересекается с горизонтальной плоскостью по прямой АВ. Угол между плоскостями α=30º. Маленькая шайба начинает движение вверх по наклонной плоскости из точки А с начальной скоростью u0= 2 м/спод углом β=60º к прямой АВ. В ходе движения шайба съезжает на прямую АВ в точке В. Пренебрегая трением между шайбой и наклонной плоскостью найдите расстояние АВ.
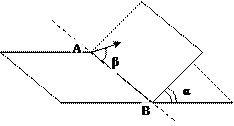
Указание: для решения задачи следует рассмотреть траекторию движения шайбы –параболу лежащую на наклонной плоскости и выбрать оси координат см. рис.
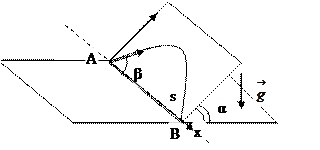
|
В т.В х=s и уравнение х(t) имеет вид s=uocos60ºt
Найти t можно из уравнения у(t), в этой точке оно будет иметь вид 0=uosin60ºt – 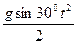 . Решая совместно эту систему уравнений найдите s.
. Решая совместно эту систему уравнений найдите s.
Ответы к обучающим заданиям.
| 1А | 2А | 3А | 4А | 5А | 6А | 7А | 8А | 9А | 10А |
| 11А | 12А | 13А | 14А | 15А | 16А | 17В | 18В | 19В | 20С |
| 69 см |
Дата добавления: 2016-07-18; просмотров: 4587;