Электрические и магнитные мультипольные гамма-переходы

Образование γ-квантов происходит под действием электромагнитных сил и обусловлено взаимодействием отдельных нуклонов ядра с электромагнитным полем, создаваемым движением всех нуклонов ядра. Поэтому γ-излучение, в отличие от β-распада, явление внутриядерное, а не внутринуклонное. Испускание или поглощение g-квантов свободным нуклоном запрещено совместным действием законов сохранения энергии и импульса.

Собственный механический момент g-кванта равен единице s=1. Это обусловлено тем, что электромагнитные колебания происходят в плоскости, перпендикулярной вектору перемещения волны (поперечные колебания) и поэтому не может быть сферической симметрии, которая в квантовой механике характеризуется нулевым механическим моментом. В этой связи g-кванты, испускаемые ядрами, должны уносить из ядра момент импульса не меньше единицы. Для фотона вообще, имеющего нулевую массу покоя, в отличие от других микрочастиц, не существует понятия орбитального момента, и у фотона нет s-, p-, d- и других состояний с определенными значениями орбитального момента l. Фотон может обладать только полным моментом J = 1, 2, 3… J ≠ 0. Состояние свободно распространяющегося электромагнитного поля с определенным полным моментом J и четностью P называется мультиполем. J - мультипольность. Излучение, уносящее момент J = 1, называется дипольным, J= 2 – квадрупольным J = 3 - октупольным и т.д. Монопольных g-квантов J = 0 не существует. Для радиационных переходов определенной мультипольности используются следующие обозначения. Радиационные переходы, вызванные перераспределением электрических зарядов в ядре, называют электрическими и обозначают буквой E (E1 - дипольные (J = 1), Е2 - квадрупольные (J = 1), и т.д.), переходы, вызванные перераспределением магнитных моментов нуклонов называют магнитными переходами (дипольные - M1, квадрупольные - М2 и т.д.). Для большинства ядер время жизни дипольных переходов τ = 10^-12 до 10^-17с.

В соответствии с законом сохранения полного момента количества двидения ( 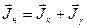) существует следующие соотношение между спином J_н начального и спином J_к конечного ядра и моментом J, уносимым g‑квантом:

.

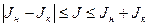(16.5)

Это соотношение называется правилом отбора по спину. Согласно этому соотношению дипольные γ‑кванты (J = 1) могут быть испущены при переходах между состояниями с ΔJ= 0, ±1, кроме (0-0)-переходов; квадрупольные γ‑кванты (J= 2) – при переходах с ΔJ= 0, ±1, ±2, кроме (0-0)-, (0-1)- и(1-0)-переходов; октупольные γ‑кванты (J= 3) – при переходах с ΔI = 0, ±1, ±2, ±3, кроме (0-0)-, (0-2)- и(2-0)- и т.д.

Еще одно правило отбора по четности связано с выполнением закона сохранения четности ( 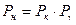). Разрешенное изменение четности Р ядра, испускающего электрический γ-квант, описывается формулой

а для ядра, испускающего магнитный γ-квант, - формулой

где Р_н иР_к – четности начального и конечного состояний ядра. Совокупность соотношений (16.5) - (16.7) обычно называют правилами отбора для γ-излучения.

Теория электромагнитного излучения дает следующие зависимости вероятности λ (постоянная распада 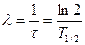) испускания g-кванта в единицу времени от мультипольности J перехода и длины волны 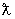(а, следовательно, и энергии g-кванта; см. (16.4)):

для электрических EJ переходов

,

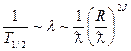(16.8)

а для магнитных HJ переходов

,

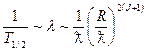(16.9)

где R – радиус ядра. Так как обычно 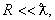то из (16.8) и (16.9) следует, что падение вероятности излучения от энергии тем резче, чем выше мультипольность, а переходы высокой мультипольности маловероятны (сильно запрещены). В основном происходит всегда излучение γ-кванта с наинизшей мультипольностью. Это связано с тем, что увеличение порядка мультипольности на единицу приводит к уменьшению вероятности излучения, т.е. вероятности γ-перехода в 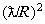раз. Кроме того, при одинаковых мультипольностях вероятность магнитного излучения тоже в 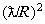раз меньше. Таким образом, в порядке уменьшения вероятности излучения переходы располагаются следующим образом: Е1, Е2 и М1, Е3 и М2 и т.д.