Function integral_1(x)

integral_1 = x ^ 2 + 1

End Function

С помощью модуля VBA, в данном случае с именем integral_1, в ячейках C6:C16 формируется спектр значений подынтегральной функции от аргумента X, и строится график этой функции.

В ячейках A6:A16, начиная с 0, указываются номера пар значений подынтегральной функции и аргумента X. В рассматриваемом примере, в соответствии с результатом вычисления арифметического выражения ячейки H4, нумерация оканчивается числом 10.

В ячейку D6 записывается арифметическое выражение =C6*$F$4, соответствующее формуле вычисления площади первого прямоугольника y₀H в площади искомой фигуры.

Содержимое ячейки D6 копируется до ячейки D15 включительно, формируя вычисление, площадей, в данном случае 10, прямоугольников, образующих площадь искомой фигуры.

Прямоугольник с последней y_N ординатой не образуется, так как это будет одиннадцатый прямоугольник.

В ячейку D18 записывается арифметическое выражение, соответствующее формуле 1.1.3, =СУММ(D6:D15).

Результатом вычисления этого арифметическое выражения является число

1,28500000, это и есть значение определённого интеграла, соответствующего варианту задания и найденного по формуле левых прямоугольников в среде Excel.

Для нахождения значения определённого интеграла, соответствующего варианту задания и вычисленного по формуле левых прямоугольников в среде VBA,необходимо предварительно создать модуль VBA, реализующий алгоритм, соответствующий формуле 1.1.3.

Function Prym(a As Double, b As Double, n As Integer)

h = (b - a) / n

Prym = 0

For i = 0 To n - 1

Prym = Prym + integral_1(a + i * h)

Next i

Prym = Prym * h

End Function

При вызове модуля Prym(a, b, n) из ячейки D19 появляется окно Аргументы функции, рис. 1.1.3.

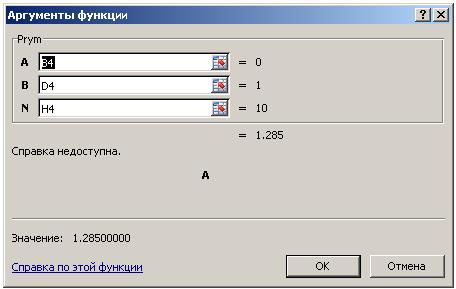
Рис. 1.1.3

После подстановки в качестве аргументов значений ячеек B4, D4 и H4 и нажатии кнопки ОКв ячейке D19 отображается число 1,28500000, это и есть значение определённого интеграла, соответствующего варианту задания и найденного по формуле левых прямоугольников в среде VBA.

Совпадение результатов вычислений в ячейках D18 иD19подтверждает правильность вычислений.

Метод трапеций

Вычисление определённого интеграла

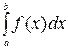(1.2.1)

в геометрической интерпретации адекватно вычислению площади фигуры, ограниченной осью абсцисс, ординатами, восстановленными из точек оси абсцисс соответствующих пределам интегрирования и отрезком подынтегральной функции, рис. 1.2.1.

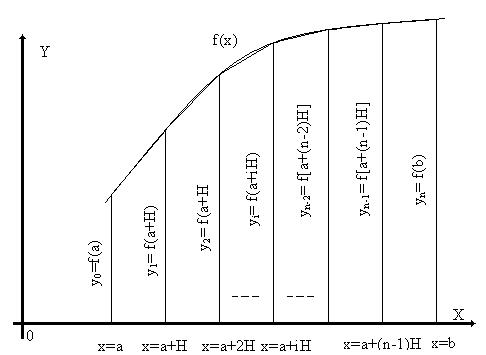
Рис. 1.2.1

Вычисление определённого интеграла методом трапеций заключается в разбиении промежутка [a;b] на n равных частей, длина каждой части H определяется по формуле

, (1.2.2)

построении трапеций, как показано на рис. 1.2.1, и замене площади искомой фигуры суммой площадей трапеций.

При этом реализуется формула

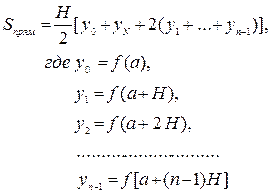(1.2.3)

Результат решения задачи представлен на рис. 1.1.2.

В дополнение к операциям, выполненным в разделе 1.1, в ячейку E6 записывается арифметическое выражение =(C6+C7)/2*$F$4, соответствующее формуле вычисления площади первой трапеции (y₀ + y1)/2*H в площади искомой фигуры.

Содержимое ячейки E6 копируется до ячейки E15 включительно, формируя вычисление площадей, в данном случае 10, трапеций, образующих площадь искомой фигуры.

Трапеция с последней y_N ординатой и ординатой y_N+1 не образуется, так как это будет одиннадцатая трапеция.

В ячейку E18 записывается арифметическое выражение, соответствующее формуле 1.2.3, =СУММ(E6:E15).

Результатом вычисления этого арифметическое выражения является число

1,33500000, это и есть значение определённого интеграла соответствующего варианту задания и найденного по формуле трапеций в среде Excel.

Для нахождения значения определённого интеграла, соответствующего варианту задания и вычисленного по формуле трапеций в среде VBA,необходимо предварительно создать модуль VBA, реализующий алгоритм, соответствующий формуле 1.2.3.