Теплообмен излучением между двумя телами, произвольно расположенными в пространстве. Угловые коэффициенты излучения

Рассмотрим два черных тела, которые имеют изотермические поверхности с температурами Т₁ и Т_2. Самооблучение их отсутствует. Теплообмен этих тел с другими телами тоже отсутствует. Тела являются однородными, изотропными. Требуется определить поток результирующего излучения.

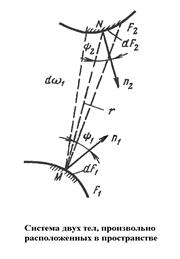Для этого на каждом из рассматриваемых тел выделяются элементарные площадки dF₁ и dF₂. Введем понятие элементарного углового коэффициента излучения

,

.

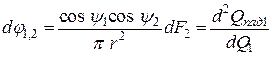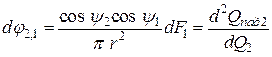Эта величина характеризует долю энергии излучения, которая попадает с элементарной площадки одного тела на элементарную площадку другого тела по отношению к полному потоку, испускаемому элементарной площадкой первого тела.

Произведение элементарного углового коэффициента излучения на площадь соответствующей элементарной площадки носит название элементарной взаимной поверхности излучения

; .

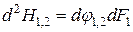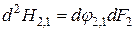Найдем местные значения потоков излучения элементарных площадок dF₁ и dF₂ на конечные поверхности, соответственно F₂ и F₁. Для этого производится интегрирование

,

.

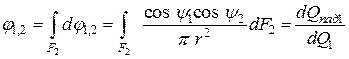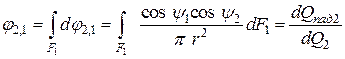Согласно записанных выражений местный угловой коэффициент излучения характеризует долю энергии, испускаемой элементарной площадкой dF₁ одного тела на конечную поверхность F₂ другого тела по отношению к полной энергии излучения, испускаемой элементарной площадкой первого тела.

Для определения средних угловых коэффициентов излучения интегрируем второй раз

; .

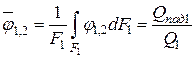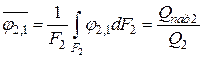Средний угловой коэффициент излучения характеризует долю энергии, которая попадает с тела, имеющего конечную площадь поверхности F₁ на другое тело с конечной площадью поверхности F₂ по отношению к полному потоку собственного излучения первого тела.

Средние взаимные поверхности излучения

; .

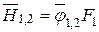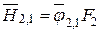По закону Стефана-Больцмана

.

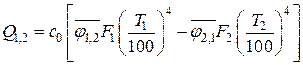Результирующий поток излучения для системы, состоящей из двух серых тел

.

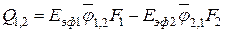Используя соотношение для эффективных потоков и свойство взаимности, получаем окончательное выражение потока результирующего излучения

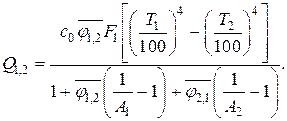
При определении потока результирующего излучения величины 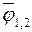, 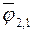рассматриваются как заданные.