Теплообмен излучением между телом и его оболочкой
Изучающая система без экранов.Рассмотрим два тела, из которых одно находится внутри другого. Первое – выпуклое, второе – вогнутое. Размеры тела заданы F1 и F2, поглощательные способности A1 и A2, а также температуры поверхностей T1 и T2, причем T1 >T2. Используя уравнение для результирующей плотности теплового потока, при наличии диатермичной среды
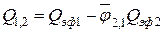 ,
,
где 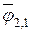 - средний угловой коэффициент излучения.
- средний угловой коэффициент излучения.
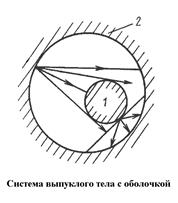 Он характеризует часть потока эффективного излучения, который попадает со второго тела на первое по отношению к полному потоку эффективного излучения второго тела. Угловой коэффициент
Он характеризует часть потока эффективного излучения, который попадает со второго тела на первое по отношению к полному потоку эффективного излучения второго тела. Угловой коэффициент 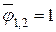 , так как вся излучаемая энергия первого тела попадает на второе тело. Угловой коэффициент
, так как вся излучаемая энергия первого тела попадает на второе тело. Угловой коэффициент 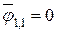 , так как тело выпуклое. Величина
, так как тело выпуклое. Величина 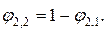
Для определения потока результирующего излучения используем метод сальдо
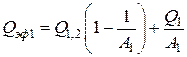 ,
,
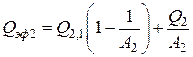 .
.
Учитывая, что при стационарном режиме результирующие потоки равны
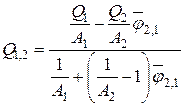 .
.
Потоки собственного излучения могут быть выражены по закону Стефана-Больцмана через заданные температуры
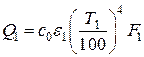 ;
; 
 .
.
С учетом вышеуказанного, получаем
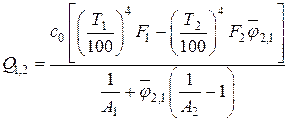 .
.
Для определения неизвестных значений 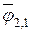 положим временно, что температуры тел 1 и 2 одинаковы. В этом случае
положим временно, что температуры тел 1 и 2 одинаковы. В этом случае 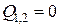 . Знаменатель не может быть равен нулю,
. Знаменатель не может быть равен нулю, 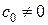 , Т1≠0, Т2≠0. Тогда,
, Т1≠0, Т2≠0. Тогда, 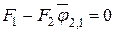 . Откуда
. Откуда
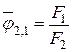 .
.
Средний угловой коэффициент превращается в чисто геометрическую характеристику.
Выражение для результирующего потока излучения примет вид
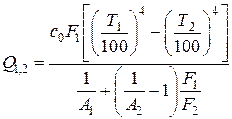 .
.
Введем понятие приведённой излучательной способности системы, Вт/(м2К4)
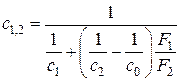 .
.
Тогда, выражение для результирующего потока излучения
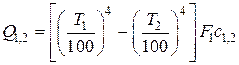 .
.
Дата добавления: 2016-07-11; просмотров: 2661;











