Кинетостатическое исследование механизма
Задача кинетостатики сводится к определению внутренних сил механизма, возникающих в его кинематических парах, и движущего момента, приложенного к ведущему звену и необходимого для привода в движение механизма рабочей машины или момента сопротивления, приложенного к ведомому валу и преодолеваемого исследуемым механизмом двигателя. Необходимость определения усилий в кинематических парах связана с задачами расчета звеньев и элементов кинематических пар на прочность, создания оптимального варианта конструкции механизма, определения коэффициента полезного действия машины, ее уравновешивания на фундаменте и т.п. Движение всякого механизма происходит под действием внешних сил, к которым относятся движущие силы; силы полезного (производственного) сопротивления, силы вредного сопротивления (трения, сопротивления среды и т.п.), силы веса звеньев и силы инерции их.
В быстроходных машинах ускорения звеньев могут достигать значительных величин и динамические усилия в кинематических парах механизма могут многократно превышать усилия от статического нагружения. В подобных случаях пренебрегать влиянием динамических нагрузок недопустимо. Одним из распространенных методов силового исследования механизма с учетом сил инерции является метод кинетостатики, основанный на использовании принципа Даламбера, сущность которого заключается в том, что каждое звено может рассматриваться в условном статическом равновесии, если к нему будут добавлены силы инерции.
В общем случае инерционная нагрузка на звено может быть сведена к силе инерции, результирующий вектор которой равен произведению массы звена 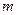 на ускорение центра масс звена
на ускорение центра масс звена 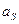
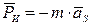 ,
,
и направлен противоположно ускорению центра масс звена, и паре сил инерции с моментом, равным по модулю произведению момента инерции звена относительно оси, проходящей через центр его масс 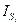 на угловое ускорение звена
на угловое ускорение звена 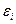
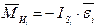 ,
,
направленным противоположно угловому ускорению звена.
В итоге расчетные уравнения кинетостатики будут иметь вид
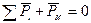 ,
,
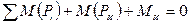 .
.
Порядок кинетостатического исследования механизма заключается в последовательном рассмотрении условий равновесия групп Ассура, начиная с наиболее удаленной от входного звена, в результате которого определяются реакции связей, являющихся усилиями во внешних кинематических парах, возникающих вследствие освобождения группы от примыкающих звеньев механизма. Эта задача всегда разрешима в силу статической определимости групп Ассура. Действительно, считая, что для каждого звена можно составить 3 уравнения равновесия, а для 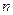 звеньев
звеньев 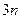 уравнений и учитывая, что реакция каждой кинематической пары 5 класса содержит 2 неизвестных (модуль и направление), то условие статической определимости получит вид
уравнений и учитывая, что реакция каждой кинематической пары 5 класса содержит 2 неизвестных (модуль и направление), то условие статической определимости получит вид
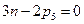 .
.
Последнее выражение совпадает с известным условием существования групп Ассура.
Силовой расчет механизма проводится с учетом всех действующих внешних сил, за исключением сил трения, влиянием которых ввиду малости можно пренебречь. Наряду с заданной силой сопротивления или движущей силой (для ДВС) и силами веса звеньев к известным внешним силам относятся силы инерции и моменты пар сил инерции.
Значения движущих сил 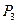 и
и 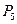 , берём с индикаторной диаграммы, не забывая о том, какой такт происходит в цилиндре, для заданного положения механизма
, берём с индикаторной диаграммы, не забывая о том, какой такт происходит в цилиндре, для заданного положения механизма  Н;
Н; 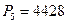 Н.
Н.
Определим модули сил инерции звеньев и моментов пар сил инерции.
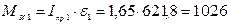 ,
,
где 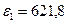
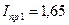 [кг∙м2] (
[кг∙м2] ( 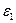 и
и 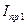 определяются при выполнении динамического синтеза механизма)
определяются при выполнении динамического синтеза механизма)
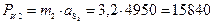 Н,
Н,
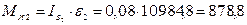 Н∙м,
Н∙м,
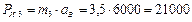 Н,
Н,
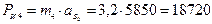 Н,
Н,
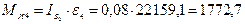 Н∙м,
Н∙м,
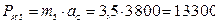 Н.
Н.
Приложены результирующие векторы сил инерции в центрах масс соответствующих звеньев и направлены противоположно вектору ускорения центра масс звена. Направление моментов пар сил инерции звеньев противоположно угловым ускорениям звеньев.
Силы веса звеньев определим
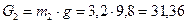 H,
H, 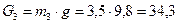 H,
H,
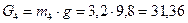 H,
H, 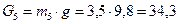 H.
H.
Вследствие того, что силы веса звеньев очень малы по сравнению с другими силами, то можно ими пренебречь.
Силовой (кинетостатический) расчет начинаем с последней присоединенной группы Ассура (4,5). Отсоединяем ее от механизма и вычерчиваем в масштабе 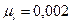 м/мм. Покажем действующие на нее внешние силы и силы реакций, возникающих в разорванных кинематических парах. Действие отброшенной стойки заменим реакцией
м/мм. Покажем действующие на нее внешние силы и силы реакций, возникающих в разорванных кинематических парах. Действие отброшенной стойки заменим реакцией 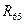 , которая направлена по перпендикуляру к направляющей и приложена в точке
, которая направлена по перпендикуляру к направляющей и приложена в точке 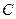 , т.к. линии действия всех сил, действующих на звено 5, проходят через ось шарнира
, т.к. линии действия всех сил, действующих на звено 5, проходят через ось шарнира 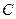 . Реакцию в шарнире
. Реакцию в шарнире  –
– 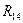 разложим на составляющие:
разложим на составляющие: 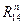 – нормальная составляющая, направленная вдоль звена
– нормальная составляющая, направленная вдоль звена 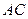 и
и 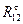 – тангенциальная – по перпендикуляру к звену
– тангенциальная – по перпендикуляру к звену 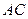 .
.
Составляем уравнение равновесия для группы (4,5).
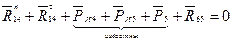
В уравнении 3 неизвестных. Составляющую 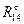 определим из уравнения моментов всех сил, действующих на звено 4 относительно точки
определим из уравнения моментов всех сил, действующих на звено 4 относительно точки 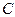 .
.
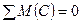 ;
; 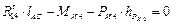 .
.
Для определения плеча силы опускаем перпендикуляр из точки 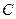 на линию действия силы, замеряем его и умножаем на масштабный коэффициент
на линию действия силы, замеряем его и умножаем на масштабный коэффициент 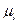 .
.
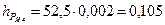 м;
м;
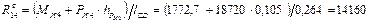 Н.
Н.
Если в результате расчета реакция 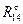 получается со знаком минус, то выбранное направление следует изменить на противоположное.
получается со знаком минус, то выбранное направление следует изменить на противоположное.
После определения 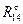 в уравнении остаются неизвестными величины сил
в уравнении остаются неизвестными величины сил 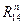 и
и 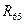 , и по векторному уравнению можно построить векторный многоугольник сил. Выбираем для построения масштабный коэффициент сил
, и по векторному уравнению можно построить векторный многоугольник сил. Выбираем для построения масштабный коэффициент сил 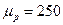 Н/мм. Тогда отрезки изображающие силы на чертеже определятся делением величины силы на
Н/мм. Тогда отрезки изображающие силы на чертеже определятся делением величины силы на 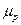 .
.
Например: 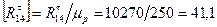 мм.
мм.
Из произвольно выбранной точки 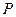 последовательно откладываем вектора сил в соответствии с уравнением, начиная с
последовательно откладываем вектора сил в соответствии с уравнением, начиная с 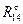 . Отложив все известные силы, из точки
. Отложив все известные силы, из точки 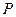 проводим направление
проводим направление 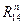 параллельно звену
параллельно звену 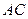 , а из конца вектора силы
, а из конца вектора силы 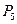 – линию действия
– линию действия 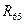 перпендикулярную направляющей
перпендикулярную направляющей 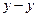 . Точка пересечения этих направлений отмерит искомые реакции. Замерив полученные отрезки и умножив на
. Точка пересечения этих направлений отмерит искомые реакции. Замерив полученные отрезки и умножив на 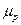 , получим реальные величины реакций.
, получим реальные величины реакций.
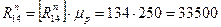 H,
H,
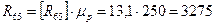 H.
H.
Просуммировав векторы сил 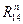 и
и 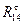 определяем полную реакцию
определяем полную реакцию 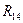 .
.
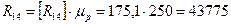 Н.
Н.
Для определения реакции 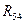 во внутренней кинематической паре рассмотрим равновесие четвертого звена:
во внутренней кинематической паре рассмотрим равновесие четвертого звена:
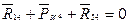
На построенном векторном многоугольнике сил соединяем начало вектора 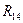 с концом вектора
с концом вектора 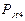 . Полученный отрезок определит величину
. Полученный отрезок определит величину 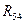 .
.
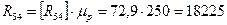 Н.
Н.
Отсоединяем от механизма группу Ассура (2,3) и вычерчиваем в масштабе 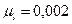 м/мм. Покажем действующие на нее внешние силы и силы реакций, возникающих в разорванных звеньях. Действие отброшенной стойки заменим реакцией
м/мм. Покажем действующие на нее внешние силы и силы реакций, возникающих в разорванных звеньях. Действие отброшенной стойки заменим реакцией 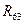 , которая направлена по перпендикуляру к направляющей и приложена в точке
, которая направлена по перпендикуляру к направляющей и приложена в точке 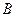 , так как линии действия всех сил действующих на звено 3 проходят через ось шарнира
, так как линии действия всех сил действующих на звено 3 проходят через ось шарнира 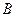 . Реакцию в шарнире
. Реакцию в шарнире 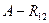 разложим на составляющие:
разложим на составляющие: 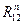 – нормальная составляющая, направленная вдоль звена
– нормальная составляющая, направленная вдоль звена 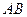 и
и 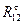 – тангенциальная составляющая – по перпендикуляру к звену
– тангенциальная составляющая – по перпендикуляру к звену 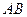 .
.
Составляем уравнение равновесия для группы (2,3):
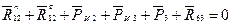
В уравнении 3 неизвестных. Составляющую 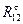 определим из уравнения моментов всех сил, действующих на звено 2 относительно точки
определим из уравнения моментов всех сил, действующих на звено 2 относительно точки 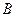 .
.
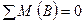 ,
, 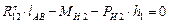 .
.
Для определения плеча силы опускаем перпендикуляр из точки 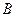 на линию действия силы, замеряем его и умножаем на масштабный коэффициент
на линию действия силы, замеряем его и умножаем на масштабный коэффициент 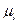 .
.
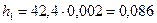 м.
м.
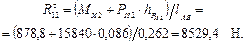
Если в результате расчета реакция 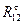 получается со знаком минус, то выбранное направление следует изменить на противоположное.
получается со знаком минус, то выбранное направление следует изменить на противоположное.
После определения 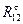 в уравнении остаются неизвестными величины
в уравнении остаются неизвестными величины 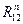 и
и 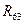 , и по векторному уравнению можно построить векторный многоугольник сил. Начинаем с
, и по векторному уравнению можно построить векторный многоугольник сил. Начинаем с 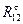 , отложив все известные силы из точки
, отложив все известные силы из точки 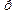 проводим направление
проводим направление 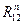 параллельно звену
параллельно звену 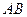 , а из конца вектора силы
, а из конца вектора силы 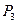 линию действия
линию действия 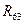 перпендикулярную направляющей
перпендикулярную направляющей 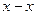 . Точка пересечений этих направлений отмерит искомые реакции, замерив полученные отрезки и умножив на
. Точка пересечений этих направлений отмерит искомые реакции, замерив полученные отрезки и умножив на 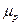 , получим реальные величины реакций:
, получим реальные величины реакций:
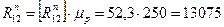 H,
H,
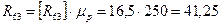 H.
H.
Просуммировав векторы сил 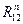 и
и 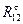 , определяем полную реакцию
, определяем полную реакцию 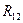
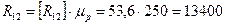 Н.
Н.
Для определения реакции 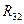 во внутренней кинематической паре рассмотрим равновесие второго звена:
во внутренней кинематической паре рассмотрим равновесие второго звена:
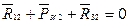
На построенном векторном многоугольнике сил соединяем начало вектора 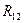 с концом вектора
с концом вектора 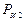 . Полученный отрезок определит величину
. Полученный отрезок определит величину 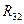 .
.
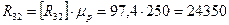 Н.
Н.
Заканчивается силовой анализ рассмотрением механизма первого класса состоящего из начального звена и стойки, которые образуют между собой вращательную кинематическую пару пятого класса.
Из условия статической определимости кинематической цепи следует, что под действием приложенных сил механизм 1 класса не находится в равновесии, т.к. при числе подвижных звеньев, равном единице, и числе кинематических пар 5 класса равном единице, число уравнений равновесия, которое мы можем составить, на единицу больше числа неизвестных.
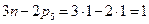
Чтобы имело место равновесие, необходимо дополнительно ввести силу или пару сил, уравновешивающую все силы, приложенные к входному звену. Эта сила или момент пары сил носят название уравновешивающей силы 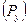 или уравновешивающего момента
или уравновешивающего момента 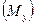 . Если вращение на кривошип в рабочей машине передается через зубчатую передачу, то для выполнения равновесия необходимо приложить уравновешивающую силу
. Если вращение на кривошип в рабочей машине передается через зубчатую передачу, то для выполнения равновесия необходимо приложить уравновешивающую силу 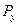 , которая будет приложена в полюсе зацепления, и линия действия ее будет совпадать с линией зацепления.
, которая будет приложена в полюсе зацепления, и линия действия ее будет совпадать с линией зацепления.
Если вращение на кривошип передается через муфту, то к ведущему звену необходимо приложить уравновешивающий момент.
Считаем, что в заданном механизме вращение с кривошипа передается через муфту, и определим уравновешивающий момент.
Вычерчиваем в масштабе 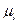 механизм 1 класса и составляем уравнение моментов относительно точки
механизм 1 класса и составляем уравнение моментов относительно точки 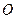 .
.
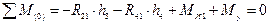
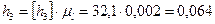 м
м
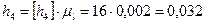 м
м
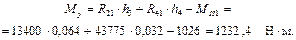
Для определения реакции в кинематической паре стойка – кривошип, отбросим стойку и рассмотрим равновесие первого звена
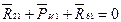
Построим векторный многоугольник сил в масштабе 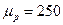 Н/мм.
Н/мм. 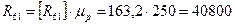 Н.
Н.
Дата добавления: 2020-07-18; просмотров: 608;











