Количественные характеристики надежности
Для количественной оценки надежности устройства используют следующие основные критерии:
- вероятность безотказной работы в течение заданного промежутка времени, P(t);
- частота отказов, a(t);
- интенсивность отказов, λ(t);
- средняя наработка до первого отказа, Tср;
- наработка на отказ, tср.
Между перечисленными критериями надежности существуют аналитические зависимости.
Вероятность безотказной работы является убывающей функцией времени и обладает следующими свойствами
0≤P(t)≤1; P(0)=1; P(∞)=0.
Величина, равная 1− P(t)=Q(t), (386)
называется вероятностью отказаи означает вероятность того, что в заданном интервале времени и определенных условиях эксплуатации произойдет хотя бы один отказ.
P(t)+Q(t)=1. При этом Q(∞)=1, а Q(0)=0.
Частотой отказов, a(t),называют число отказов в единицу времени, отнесенное к первоначальному числу образцов устройств, установленных на испытания.
a(t)=∆n(t)/(n∙∆t), (387)
где ∆n(t) - число отказавших образцов устройств в интервале времени ∆t;
n - число образцов устройств, установленных на испытания.
Частота отказов a(t) является плотностью вероятности отказов, равным
dQ(t)/dtили, согласно выражения (386), является производной от надежности, взятой с обратным знаком
a(t)=f(t)= dQ(t)/dt=−dP(t)/dt. (388)
Отсюда вероятность отказа устройства
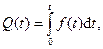 (389)
(389)
а вероятность безотказной работы устройства
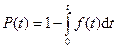 (390)
(390)

Рис.230. Зависимость вероятности безотказной работы во времени
Отметим, что частота отказовa(t)или плотность вероятности их f(t)характеризует надежность устройства до первого его отказа (ремонтируемого устройства) и надежность устройства в целом (в случае неремонтируемого устройства, которое после отказа не ремонтируется и не эксплуатируется).
Напомним, что интенсивностью отказов в работе устройства называется отношение числа отказавших образцов в единицу времени к среднему числу их, исправно работающих в данном отрезке времени:
λ(t)=∆n(t)/(nср∙∆t), (391)
где nср=(ni+ni+1)/2 - среднее число исправно работающих образцов устройств в интервале времени ∆t;
ni - число исправно работающих образцов в начале интервала времени ∆t;
ni+1 - то же, но в конце интервала времени ∆t.
Отметим, что nср<n, поэтому формула (387) не равна формуле (391),т.е.
a(t) < λ(t).
С другой стороны интенсивностью отказов λ(t)называется также и отношение плотности вероятности отказов f(t)к надежности P(t),что с учетом уравнения (4) дает
λ(t)=f(t)/P(t)=−[dP(t)/dt]/P(t). (392)
Откуда после интегрирования получим
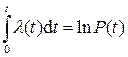 .
.
Тогда надежность устройства определим по формуле
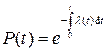 (393)
(393)
На основании (388),(392) и (393) частота отказов a(t) или плотность вероятности этих отказов f(t)могут быть представлены в виде
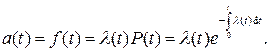 (394)
(394)
Как показывает уравнение (392) в общем случае интенсивность отказов λ(t) за период работы устройства является переменной величиной и, следовательно, надежность ее согласно уравнению (393) в этом случае будет убывать с течением времени не по экспоненциальной кривой.
Уравнение (392) является наиболее общим выражением для определения интенсивности отказов λ(t).
Оно справедливо для всех возможных распределений отказов как экспоненциальных, так и неэкспоненциальных. В нем интенсивность отказов является функцией времени t работы устройства т.к. надежность ее P(t)и степень убывания надежности [dP(t)/dt]являются также функцией времени.
Только в одном случае – при экспоненциальном характере убывания надежности во времени – величина λ(t) в уравнении (392) оказывается постоянной величиной
P(t)=℮-λ*t , (395)
где λ - средняя постоянная времени интенсивности внезапных отказов устройства в долях единицы на один час работы,
t - произвольное время работы устройства в часах, для которого определяется его надежность.
Степень убывания надежности во времени согласно уравнению (388) представляет собой плотность вероятности отказов f(t).
В частности, когда интенсивность отказов λ- величина постоянная, плотность вероятности отказов f(t)согласно уравнению (388) и с учетом формулы (395) будет
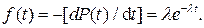 (396)
(396)
На рис. 231 представлена экспоненциальная кривая плотности вероятности отказов f(t) по уравнению (396) в зависимости от времени работы устройства.
Так как в этом случае, с учетом (396) интеграл
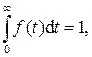
то вероятностьбезотказной работы согласно (390) можно представить в виде
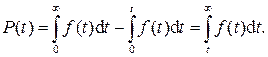 (397)
(397)
Таким образом, заштрихованная часть площади под кривой f(t) в интервале от t до ∞ представляет собой значение вероятности безотказной работыP(t),
а незаштрихованная часть площади от 0 до t представляет согласно (389) -
вероятность отказа устройства Q(t).
Отметим особо, что уравнение (395) справедливо для устройств, прошедших приработку и уже не обнаруживают «приработочных» отказов, но также и не испытывающих еще влияние износа. Этот период принято называть периодом нормальной эксплуатации устройства.
Прервем на некоторое время рассмотрение вопросов надежности и рассмотрим более подробно периоды работы устройства.
Принято выделять три периода «жизни» устройства (электрической машины, полупроводникового преобразователя и т.п.).:
1 - период приработки;
2 - период нормальной эксплуатации;
3 - период старения (износа).
Понятно, что главным периодом жизни устройства является период нормальной эксплуатации.
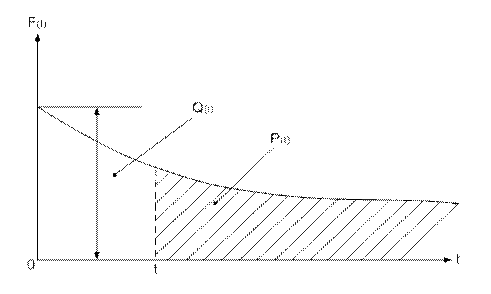
Рис. 231.Зависимость плотности вероятности отказов во времени
Период нормальной эксплуатации. В этот период происходят внезапные отказы, которые носят случайный характер. Физическая природа этих отказов обусловлена внезапной концентрацией нагрузок, действующих внутри и вне устройства (ЭП). Случайность возникновения внезапных отказов проявляется в том, что события происходят неожиданно и нерегулярно. Однако в достаточно большие и приблизительно равные промежутки времени они повторяются
примерно с одинаковой интенсивностью.
Устранить внезапные отказы в работе устройства практически не представляется возможным, но предупредить их и принять меры к уменьшению их во время основной работы устройства - можно.
Период старения.В этот период отказы вызываются износом отдельных частей (узлов) устройства (машины). Они возникают главным образом в устройствах, которые длительно работают без ремонта или неправильно эксплуатируются. Отказы из-за износа деталей машины являются признаком старения ее. Во многих случаях отказы в работе машины за счет износа ее деталей могут быть ограничены путем своевременной замены их новыми во время ремонта машины, а также правильными режимами работы, мерами ухода за машиной.
Следовательно, если на практике налажено систематическое профилактическое обслуживание устройства, то надежная работа его возможна в течение очень длительного времени. Устройства с правильно выбранными периодами профилактического ремонта очень длительное время не стареют и поэтому не будут отказывать в работе из-за износа.
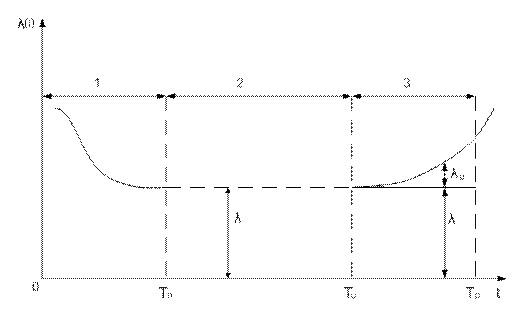
Рис.232. Кривая интенсивности отказов для трех периодов работы устройства
Период приработки.В этот период при испытании устройства (ЭП) происходит отбраковка конструктивных, технологических и производственных дефектов. Отказы в период времени приработки от 0 до Тп в дальнейшем не оказывают влияния на надежность устройства в период нормальной эксплуатации его с момента от t =Tп до t=Tи. Приработочные отказы устраняются в течение первого периода работы устройства обычно путем замены дефективных деталей исправными или их приработки.
Среднее условное время исправной работы устройства от начала периода нормальной эксплуатации (от Тп) до первого отказа в работе при условии отсутствия износа носит название средняя наработка до первого отказа устройства, Тср.
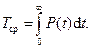 (398)
(398)
Cледовательно, средняя наработка до первого отказа, или среднее время
безотказной работы, называемое в теории вероятности математическим ожиданием времени безотказной работы, численно характеризуются площадью под кривой надежности P(t) (рис.230).
Для случая интенсивности внезапных отказов λ=const средняя наработка до первого отказа устройства по уравнению (398) с учетом (395), получается
Тср=1/λ, час. (399)
Эта величина в общем случае может характеризовать также среднее значение времени tср между соседними отказами в работе устройства. Такое время принято называть наработкой на отказ.Эта величина определяется из статистических данных об отказах устройств следующим образом:
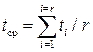 час. (400) где r - число отказов устройства за время t;
час. (400) где r - число отказов устройства за время t;
ti - время исправной работы устройства между (i-1) и (i) отказами.
Как показывает уравнение (400) наработка на отказ tср является средним временем между двумя соседними отказами устройства и при λ=const эта величина равна средней наработке до первого отказа Тср.
Отметим, что Тср не имеет ничего общего с фактическим сроком службы ЭП. При λ=const надежность ЭП:
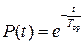 (401)
(401)
Кривая надежности устройства, построенная по формуле (401), носит название стандартная кривая надежности - приведена на рис.234, а ее верхняя часть на рис. 235 (для времени t<(Тср/10).
При t<(Тср/10) Вероятность безотказной работы Р(t)=0,90, при t=(Тср/10)→Р(t)=0,99. При t=Тср/1000 →P(t)=0,999. Надежность устройства с P(t)=0,999 означает, что из 1000 одинаковых образцов, проработавших
t= Тср/1000 часов, приблизительно 999 образцов будут исправными, а один образец откажет.
Вывод: Таким образом, вероятность безотказной работы Р(t), частота отказов a(t), интенсивность отказов λ(t), средняя наработка до первого отказа Тср и наработка на отказ tср являются основными техническими характеристиками надежности любых устройств.
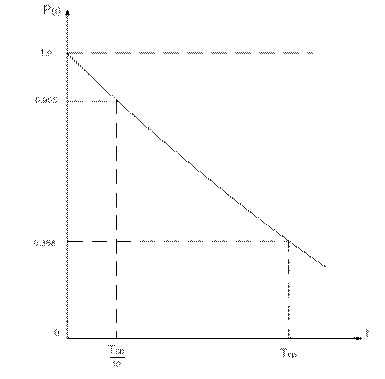
Рис.234. Стандартная кривая надежности
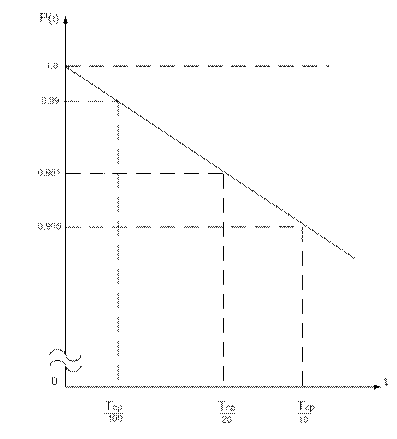
Рис.235. Верхняя часть стандартной кривой надежности
Дата добавления: 2019-02-08; просмотров: 967;











