Надежность систем из последовательно и параллельно соединенных элементов
Современные электрические приводы являются сложными техническими устройствами, состоящими из следующих основных элементов (узлов), определяющих ее работоспособность:
- электрической машины;
- полупроводникового преобразователя;
- системы управления;
- механизма передачи (редуктора);
- системы защиты и диагностики.
Совершенно очевидно, что при отказе какого- либо элементов (узлов) из перечисленных выше частей ЭП выходит из строя. Причем каждый из этих элементов (узлов) имеет свой уровень надежности. Для расчета вероятности безотказной работы ЭП, как целого устройства, в течение заданного промежутка времени нужно знать к какому типу соединения (с точки зрения теории надежности) принадлежит комбинация этих элементов – к последовательному или параллельному типу.
Отметим, что ЭП обычно рассматривают как устройство из последовательного соединения названных выше элементов, поскольку отказ в работе любого из них всегда приводит к остановке ЭП.
При последовательном соединении n элементов или блоков в системе, а также составных частей в устройстве надежность системы или устройства определяется по следующей формуле:
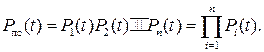 (401)
(401)
где Pi(t)-надежность i-го элемента или блока в последовательном соединении. Здесь надежность Pi(t) может быть как экспоненциальной, так и неэкспоненциальной функцией.
Вероятность отказа системы или устройства, состоящих из n последовательно соединенных элементов или блоков, Qпс(t):
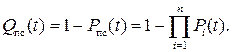 (402)
(402)
В том случае, когда надежность всех элементов в системе или устройстве изменяется во времени по экспоненциальному закону, уравнение (18) приобретает вид:
Pпс(t)= ℮-λ1t ∙ ℮-λ2t ∙ ℮-λnt ∙…= ℮-(λ1+ λ2+.. λn)t (403)
где λ1, λ2,…,λn - средние постоянные величины интенсивностей отказов отдельных элементов или составных частей устройства в долях единицы на один час работы;
t - время работы элемента или части устройства в часах.
При параллельном соединении одновременно работающих элементов или блоков в системе вероятность отказа системы Qпр(t):
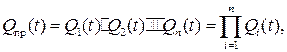 (404)
(404)
где Qi(t) =1-Pi(t) - вероятность отказа i-го элемента или блока в параллельном соединении.
Надежность системы из n параллельно работающих в ней элементов или блоков
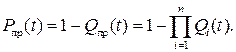 (405)
(405)
Если параллельно работающие элементы в системе одинаковы, то
Qпр(t)= Qn (t) ; (406)
Pпр(t)=1- Qn (t). (407)
Расчет надежности устройства можно проводить двумя методами.
Первый метод основан на использовании абсолютных значений интенсивности отказов всех элементов устройства. Значения интенсивности отказов отдельных элементов электроприводов приведены в табл.19.
Рассмотрим пример расчета конструкционной надежности электрической машины по первому методу расчета, воспользовавшись известными абсолютными значениями интенсивности отказов всех элементов устройства.
Таблица 19. Интенсивность отказов элементов λ·10-6 час.-1
| Наименование элемента | Верхний предел | Среднее значение | Нижний предел |
| Электродвигатели | |||
| Асинхронные | 11,2 | 8,6 | 4,49 |
| Синхронные | 6,25 | 0,36 | 0,16 |
| Постоянного тока | - | 9/36 | |
| Исполнительные | 0,35 | 0,23 | 0,11 |
| Шаговые | 0,71 | 0,37 | 0,22 |
| Вентиляторов | 5,5 | 0,2 | 0,05 |
| Трансформаторы | |||
| Силовые | 2,08 | 1,09 | 0,12 |
| Силовые высоковольтные | 1,88 | 0,94 | 0,40 |
| Импульсные | 0,235 | 0,17 | 0,03 |
| Входные | 2,08 | 1,09 | 0,12 |
| Выходные | 0,20 | 0,09 | 0,04 |
| Средних частот | 0,31 | 0,10 | 0,035 |
| Звуковой частоты | 0,04 | 0,02 | 0,01 |
| Анодные | 0,052 | 0,025 | 0,012 |
| Сельсины | |||
| Синхронных передач | 0,61 | 0,35 | 0,09 |
| Решающих устройств | 1,14 | 1,11 | 0,89 |
| Дроссели | |||
| Низкочастотные | 0,28 | 0,175 | 0,07 |
| насыщения | 0,32 | 0,14 | 0,12 |
| Конденсаторы | |||
| Слюдяные | 0,132 | 0,075 | 0,005 |
| Электролитические | 0,29 | 0,05 | 0,003 |
| Реостаты | 0,19 | 0,13 | 0,07 |
| Сопротивления проволочные | 0,126 | 0.068 | 0,038 |
| Соединения паянные | 0,005 | 0,004 | 0,0002 |
| Магниты | 7,11 | 5,65 | 2,02 |
| Магнитные усилители | 0,485 | 0,152 | 0,052 |
| Вращающиеся преобразователи | 5,46 | 2,8 | 1,15 |
| Измерительные приборы электрические | 5,77 | 0,036 | 0,005 |
| Коллекторы электрических машин | 4,85 | 2,9 | 0,97 |
| Подшипники скольжения | 0,42 | 0,22 | 0,008 |
| Подшипники шариковые | 1,72 | 0,875 | 0,035 |
| Передачи зубчатые цилиндрические | 4,3 | 2,18 | 0,087 |
| Передачи зубчатые винтовые | 0,098 | 0,05 | 0,002 |
| Передачи зубчатые редукторные | 0,36 | 0,2 | 0,11 |
| Шиты подшипниковые | 0,14 | 0,087 | 0,035 |
Таблица 20. Интенсивность отказов электродвигателей
| Тип электродвигателя | Интенсивность отказов, λ·10-4 час.-1 |
| ДПМ-20-Н3-01 | 2,0 |
| ДПМ-20-Н1-17, ДПМ-20-Н1-20 | 1,3 |
| ДПМ-20-Н1-17 | 1,4 |
| ДПМ-25-Н3-01, ДПМ-25-Н3-02, ДПМ-25-Н3-04, | 7,0 |
| ДПМ-25-Н1Т-01, ДПМ-25-Н1-02А, | 6,0 |
| ДПМ-25-Н1-01 | 3,8 |
| ДПМ-25-Н3-01, ДПМ-25-Н3-03 | 1,6 |
| ДПМ-25-Н1-02,ДПМ-25-Н1-05, ДПМ-25-Н1-07 | 2,0 |
| ДПМ-30-Н1-01 | 2,8 |
| ДПМ-35-Н1-01 | 8,0 |
| ДС-1 | 0,15 |
| ДСД-2, ДСД-60 | |
| ДПР с регулятором скорости | 0,24 |
| АПН-012/2 | 0,24 |
| АПН-11/2 | 0,4 |
| ШД-1 | 1,0 |
| ШД-300/300 | 0,75 |
ДПМ - двухполюсные ЭД постоянного тока с обычным зубчатым якорем и внешним кольцевым магнитом;
ДПР - с бескаркасным полым якорем и внутренним цилиндрическим магнитом;
ДС и ДСД - синхронный реактивно-гистерезисный двигатель;
АПН - асинхронные двигатели повышенной надежности;
ШД - шаговые двигатели.
Таблица 21. Интенсивность отказов переключателей
| Наименование элементов | λ·10-6 час-1 |
| Переключатели галетные | 0,1 |
| Выключатель ВДМ1 | 0,1 |
| Переключатель движковый ПД13 | 0,1 |
| Переключатель движковый ПД17 | 0,1 |
| Переключатель бесконтактный ПКБ9 | 0,1 |
| Держатель вставок плавких ДВП4 | 0,03 |
| Вставки плавкие ВП1 | 2,0 |
| Резисторы переменные непроволочные | 0,03 |
Задача 43:
Определить конструкционную надежность ЭМ постоянного тока для трех промежутков времени ее работы t=1000, t=3000, t=5000 часов, если средние статистические данные об интенсивности отказов основных ее частей в долях единицы на один час работы:
-индуктора λ1=0,01∙10-6 1/час ;
- якоря λ2=0,05∙10-6 1/час;
- подшипников λ3=0,4∙10-6 1/час;
- коллектора λ4=3∙10-6 1/час;
- щеточного устройства- λ5=1∙10-6 1/час.
Решение:
Средняя результирующая интенсивность отказов всех частей ЭМ
λ= λ1+ λ2+ λ3+ λ4+ λ5=(0,01+0,05+0,4+3+1) ∙ 10-6 =4,46∙10-6 1/час.
Средняя наработка до первого отказа
Тср=1/ λ=106/4,46=2,24∙105 1/час.
Вероятность безотказной работы или конструкционной надежности этой машины для трех промежутков времени
P (1000) =℮-1000/ (2,24·100000) =℮-0, 00446=0,995;
P (3000)=℮-3000/(2,24·100000) =℮-0,0144=0,988;
P(5000)=℮-5000/(2,24·100000) =℮-0,0223=0,975;
Анализ результата:
Выход из строя на каждые 1000 машин для трех промежутков времени:
- в первом случае 5 машин (0,5%);
- во втором случае 12 машин (1,2%);
- в третьем случае 25 машин (2,5%).
Как видно из приведенного примера расчет надежности электрической машины при известных абсолютных значениях интенсивности отказов всех элементов электрической машины достаточно прост и не требует существенных затрат времени.
Второй метод, называемый коэффициентным методом, основан на использовании коэффициентов надежности ki, которые связывают абсолютные значения интенсивности отказов λi с интенсивностью отказов λб какого-либо базового элемента.
Рассмотрим далее применение коэффициентного метода для расчета надежности устройства. Как уже говорилось выше, коэффициентный метод, основан на использовании коэффициентов надежности ki каждого элемента, которые связывают абсолютные значения интенсивности отказов λi с интенсивностью отказов λб какого-либо базового элемента, ki=λi/λб.
Отметим при этом, что коэффициенты надежности ki каждого элемента практически не зависят от условий эксплуатации и для данного конкретного элемента является константой, а различие условий эксплуатации учитывается посредством введения коэффициента К, который равен относительному значению интенсивности отказов базового элемента К= λ′б/ λб.
Параметр λ′б - это значение интенсивности отказов базового элемента с учетом условий эксплуатации, λ′б =К λб. Обычно в качестве базового элемента выбирается металлопленочный резистор, интенсивность отказа которого λб =0,3∙10-7 1/час.
Влияние на надежность элементов основных дестабилизирующих факторов - электрических нагрузок и температуры окружающей среды- учитываются путем введения поправочных коэффициентов. Зависимость этих коэффициентов в функции температуры окружающей среды и коэффициента нагрузки элемента по току kнi=Iраб/Iдоп, или напряжения kнu=Uраб/Uдоп,
или мощности kнр=Рраб/Рдоп в виде соответствующих графиков приведены в [5]. Учет влияния других факторов (задымленности, влажности и т.п.) выполняется путем коррекции интенсивности отказа базового элемента с помощью коэффициентов, приведенных в этом же справочнике.
Результирующий коэффициент надежности устройства k′i с учетом электрических нагрузок и температуры окружающей среды, исключая релейно-контакторную аппаратуру, определяется по формуле (408):
k′i =а1∙а2∙а3∙а4∙ki, (408)
где ki - номинальное значение коэффициента надежности;
а1 - коэффициент, учитывающий отклонение температуры окружающей среды и электрической нагрузки от номинальной;
а2 - коэффициент, учитывающий отклонение температуры окружающей среды от номинальной;
а3 - коэффициент, учитывающий снижение электрической нагрузки относительно номинальной;
а4 - коэффициент использования элемента, определяемый отношением времени работы элемента к времени работы устройства в целом.
Для релейно-контакторной аппаратуры коэффициент надежности определяется по формуле (409):
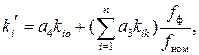 (409)
(409)
где ki,kik - коэффициенты надежности воспринимающей (цепи нагрузки) и исполнительной (контактной системы) частей аппаратуры, соответственно;
а4 - коэффициент, учитывающий время нахождения катушки аппарата под напряжением в течение одного цикла «включено-выключено» и учитывающий температуру окружающей среды;
а3 -коэффициент, учитывающий уровень электрической нагрузки контакта;
n- число контактов;
fф и fном- фактическая и номинальная частота срабатывания аппарата в час.
После определения коэффициентов надежности отдельных элементов рассчитывают показатели надежности устройства в целом.
Приведем в табл. 22 относительные значения интенсивности отказов базового элемента К= λ′б/ λб при различных условиях эксплуатации.
Таблица 22. Относительные значения интенсивности отказов базового элемента
| Условия эксплуатации системы | К= λ′б/ λб |
| Лабораторные условия эксплуатации - закрытое, отапливаемое помещение, комнатная температура, влажность не выше 65%, нормальное атмосферное давление, отсутствие запыленности, вибраций и т.п. | |
| Эксплуатация в закрытом отапливаемом помещении с повышенной влажностью, запыленностью и т.д. (например, заводские цеха, помещения подстанций и т.п.) | 2,5 |
| Тяжелые условия работы на и открытых местах, в полевых условиях на буровых установках, на летательных аппаратах т.п. |
Дата добавления: 2019-02-08; просмотров: 1173;











