Конфігурації і комплекси із точкових дефектів.
Неважко бачити, що утворення комплексів із точкових дефектів, зокрема – вакансій виявляється енергетично вигідним. Проілюструємо це наступним якісним міркуванням. Для утворення вакансії необхідно розірвати i атомних зв'язків усередині кристала та сформувати i/m зв'язків на поверхні. Припустимо тепер, що віддаляється другий атом, що є найближчим сусідом вакансії. Один зі зв'язків цього атома вже розірваний. Тому при видаленні його на поверхню повинне бути розірване i - 1 зв'язків. Отже, енергія утворення другої вакансії повинна бути
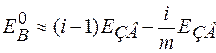 ,
,
енергія утворення дивакансій
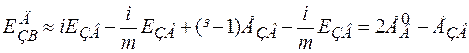 .
.
Отже, енергія утворення дивакансій рівна подвоєній енергії утворення моновакансії - мінус енергія зв'язку, що у загальному випадку називається енергією зв'язку дивакансій. Енергія зв'язку дивакансій у металевих системах має порядок 0,3 еВ, зокрема для Cu EЗВ =3.52 еВ, а значить 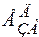
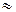 0.6 еВ (
0.6 еВ ( 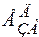 = 0.6 еВ - для благородних металів).
= 0.6 еВ - для благородних металів).
Розрахунки Вейцера і Жирифалько, показують, що дві вакансії притягуються одна до одної на відстанях менших ~7 анстрем, а на більших відстанях не взаємодіють. Тобто, дивакансії є стійкими утвореннями, хоча енергія їх зв’язку ще не досить точно розрахована. Отже, утворення вакансійних комплексів виявляється енергетично вигідним.
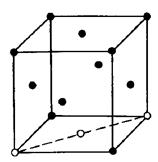
Можливі і більш великі вакансійні асоціації. На рис.2.3 показані лінійна (а) і плоска (б) конфігурації тривакансій в ГЦК- гратках.
Комп’ютерні розрахунки показують, що конфігурації тривакансій рис.2.3а) та рис.2.3б) не стійкі. Очевидно, вигідніше утворення четвертої вакансії за рахунок зсуву атомів у центр вакансійного тетраедра (тетраедрична форма тривакансій), як це показало на рис.2.3в.
Аналогічні розрахунки були проведені для тетра- та пентавакансій (рис.2.4- рис.2.6). Було встановлено, що тетраедрична форма тетравакансії є не стійкою, хоча, як було зазначено вище, у випадку тривакансій вона стійка. Релаксація одного чи більш атомів у комплексі вакансій стабілізує конфігурацію. Подібна ситуація має місце при октаедричній формі тетравакансії, за рахунок двох сильно релаксуючих атомів у центрі. Аналогічна ситуація має місце і для пентавакансії.
 а)
а) 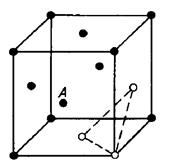 б)
б) 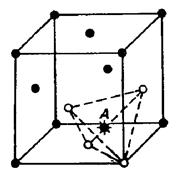 в)
в)
Рис. 2.3. Можливі конфігурації тривакансій у ГЦК - ґратках: лінійне (а), плоске (б) розташування, тетраедрична (в) конфігурації
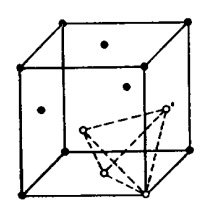
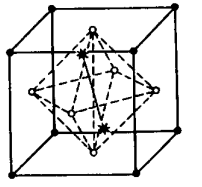
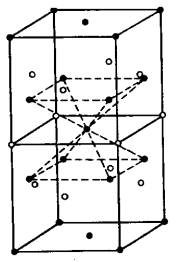
а) В = -0.1 еВ; б) В = 0.6 еВ; в) В = 0.7 еВ
Рис. 2.4. Три конфігурації тетравакансій. В- енергія зв’язку вакансій в комплексі. Конфігурація (а) є не стійкою. а - лінійне розміщення; плоска конфігурація; в - тетраедрична конфігурація, в якій атом релаксує в центр тетраедра і яка є найбільш стійкою.
Оцінимо концентрацію дивакансій, тривакансій і т.д. після, встановлення термодинамічної рівноваги. Як приклад, розглянемо однокомпонентну систему, що складається з N вузлів. Розглянемо, скількома способами можна створити в цій системі вакансійні пари. Якщо i - перше координаційне число, то на базі даного вузла в кристалічних ґратках можна створити i вакансійних пар. Якщо розглянути сусідній вузол, розташований на першій координаційній сфері стосовно першого вузла, то навколо цього вузла можливе формування також i вакансійних пар.
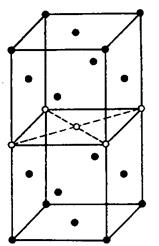
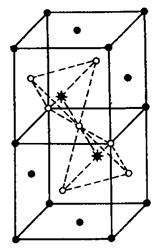
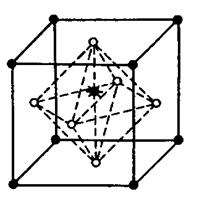
а) В = 0.7еВ; б) В = 0.9 еВ; в) В = 1.5 еВ.
Рис.2.5. Три конфігурації із пентавакансій
Віннерд, Джонсон, Браун досліджували конфігурації і стійкість комплексу із двох міжвузольних атомів, конфігурації яких представлені на рис.2.6.
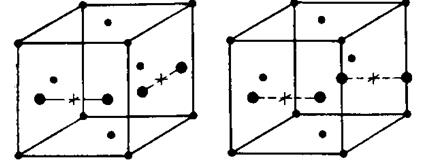
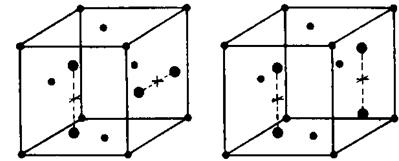
Рис.2.6. Конфігурація комплексу із двох міжвузольних атомів.
Однак із усієї сукупності отриманих у такий спосіб вакансійних пар одна буде повторюватися.
Тому якщо знехтувати азимутальним розходженням вакансійних пар, те загальне число створених вакансійних пар буде 2і-1. Якщо 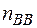 число парних вакансій, то число можливих станів
число парних вакансій, то число можливих станів
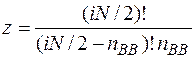 . (2.7.1)
. (2.7.1)
Застосовуючи формулу Стірлінга та процедуру, аналогічну описаній у §1 даного розділу, отримаємо
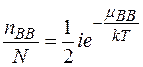 , (2.7.2)
, (2.7.2)
де ( 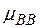 - хімічний потенціал дивакансій. Відповідно до вище сказаного
- хімічний потенціал дивакансій. Відповідно до вище сказаного 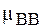 може бути представлений у виді
може бути представлений у виді
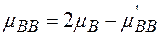 ,
,
де 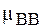 - хімічний потенціал, що характеризує зв'язок двох вакансій у комплексі. Підставляючи
- хімічний потенціал, що характеризує зв'язок двох вакансій у комплексі. Підставляючи 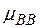 в (2.7.2), отримаємо
в (2.7.2), отримаємо
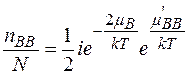 або
або 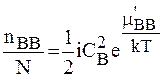 , (2.7.3)
, (2.7.3)
де 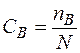 - концентрація моновакансій.
- концентрація моновакансій.
Отже, кількість дивакансій виявляється пропорційною квадрату концентрації моновакансій. Пропорційність концентрації дивакансій 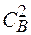 відображає наявність у системі бінарних зіткнень. З погляду кінетики це означає, що процес утворення дивакансій з моновакансій повинен описуватися реакціями другого порядку. З останнього співвідношення можна визначити частку вакансій, що з'єдналися в комплекси:
відображає наявність у системі бінарних зіткнень. З погляду кінетики це означає, що процес утворення дивакансій з моновакансій повинен описуватися реакціями другого порядку. З останнього співвідношення можна визначити частку вакансій, що з'єдналися в комплекси:
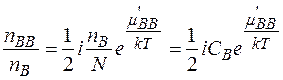 . (2.7.4)
. (2.7.4)
Зі сказаного слідує, що концентрація дивакансій з температурою росте швидше, тобто в міру підвищення температури зростає частка дефектів, об'єднаних у комплекси. Тому якщо в результаті загартування потрібно одержати головним чином ізольовані дефекти, температура загартування не повинна бути занадто великою.
Аналогічне співвідношення можна одержати для тривакансій:
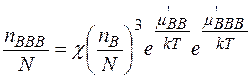 , (2.7.5)
, (2.7.5)
де 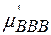 - хімічний потенціал зв'язку тривакансій; c - комбінаторний множник, що відповідає числу незалежних орієнтувань комплексу тривакансій.
- хімічний потенціал зв'язку тривакансій; c - комбінаторний множник, що відповідає числу незалежних орієнтувань комплексу тривакансій.
Що стосується концентрації більш складних комплексів, то ними можна знехтувати навіть незважаючи на велику енергію зв'язку, тому що їхня концентрація ~ 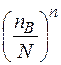 , де п — число асоційованих вакансій. Тому чим складніше комплекс, тим менше його концентрація. Фізично це означає, що чим складніше комплекс, тим менше імовірність одночасної зустрічі п вакансій, що складають даний комплекс.
, де п — число асоційованих вакансій. Тому чим складніше комплекс, тим менше його концентрація. Фізично це означає, що чим складніше комплекс, тим менше імовірність одночасної зустрічі п вакансій, що складають даний комплекс.
Контрольні питання
1. Які значення енергії утворення вакансій і дивакансій в міді?
2. Які комплекси із три-, тетра- і пентавакансій є найбільш ймовірними і стійкими?
3. Зобразити комплекси із міжвузольних атомів.
4. Від яких умов залежить утворення складних комплексів із точкових дефектів.
5. Записати співвідношення, які визначають концентрацію дивакансій, тривакансій і т.д. після встановлення термодинамічної рівноваги.
Дата добавления: 2020-07-18; просмотров: 613;











