Розупорядкування в однокомпонентних системах.

В якості прикладу розглянемо однокомпонентну систему в якій, допустимо, що в ній можуть бути тільки дефекти за Шоткі.

Будемо вважати, що хоча атом і забирається із вузла, але залишається в системі, так що сумарне число часток, які складають нормально побудовану гратку не міняється, а тому не змінюється і енергія системи, яка відповідає нормальній гратці. Тоді

,

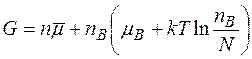де n - число часток із яких складається система; 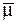- хімічний потенціал ідеальної системи в розрахунку на одну частку. Найдемо варіацію dG.

.

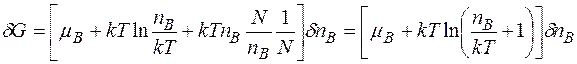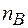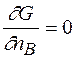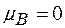Оскільки - єдина незалежна змінна, то умова рівноваги або , тобто

.

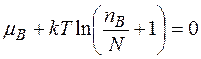Оскільки N дуже велике, т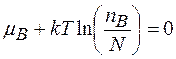о - , або

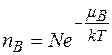(2.15)

Отримана формула дещо різниться від отриманої нами раніше, де замість E_F стоїть 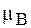. Нагадаємо, що

.

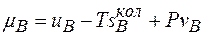В цілому 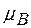залежить не тільки від об’єму, тобто коливної ентропії, але і від тиску. Отже, в загальному випадку концентрація точкових дефектів в напруженому і ненапруженому кристалах буде різною.

Розглянемо тепер випадок, коли частинка при утворенні дефекту за Шоткі не залишається в системі а віддаляється на безмежність. В цьому випадку число елементів з яких складається система змінюється. Тому потенціал G повинен бути записаний у вигляді :

.

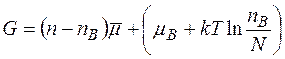Складемо варіацію

.

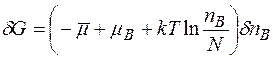Рівновага буде при умові, якщо dG=0.

Тоді для рівноважної концентрації дефектів за Шоткі

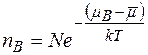. (2.16)

Зауважимо, що хімічний потенціал 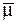ідеальної гратки від’ємний. Тому 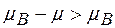, тобто концентрація точкових дефектів буде меншою.

З точки зору фізичної коректності (2.16) є більш точною, чим співвідношення (1.7) . Іншими словами процес утворення дефекту за Шоткі зводиться до переміщення структурного елементу із одного вузла гратки в інший. В такому випадку в системі нічого не зміняється. Потрібно врахувати, що при утворенні дефекту за Шоткі частка може не віддаляється зовсім і не просто повертається в систему, а приєднується на стоки. Тому тут деяка частина енергії повертається. Отже більш точна формула для підрахунку дефектів за Шоткі має вид

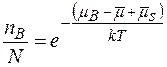, (2.16а)

де 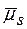- від’ємна і відповідає хімічному потенціалу елемента на стоках. Оскільки 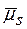< 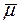, то як правило 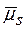опускають і виходять із (2.16).

Розглянемо систему, в якій можуть бути тільки дефекти за Френкелем. У цьому випадку

.

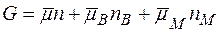
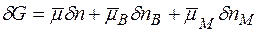По-скільки 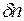, , 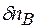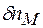не є незалежними, то не можна вважати, що

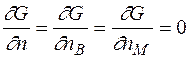
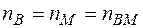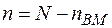У випадку дефектів Френкеля число міжвузольних атомів рівне числу вакансій і , де 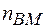- число пар вакансія - міжвузольний атом. Тому

,

.

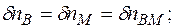
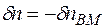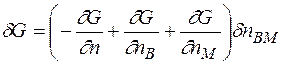Тут 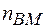- вже незалежна змінна. Тоді умову рівноваги можна записати

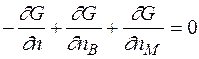
Підставивши відповідні значення похідних отримаємо

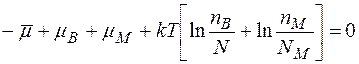
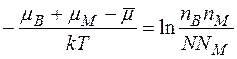
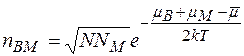(2.17)

Отже, для виникнення дефекту за Френкелем потрібно здійснити роботу для утворення вакансії плюс роботу необхідну для втілення атома.

Контрольні питання

1. Записати вираз, за допомогою якого можна оцінити зміну концентрації точкових дефектів – вакансій з температурою в кристалах

2. Від яких параметрів залежить концентрація утворення точкових дефектів за Шоткі?

3. Від яких параметрів залежить концентрація утворення точкових дефектів за Френкелем?

4. Пояснити різницю в механізмах утворення точкових дефектів за Френкелем та за Шоткі.

5. Оцінити концентрацію точкових дефектів за Шоткі і Френкелем при Т=500 ⁰С і 1000 ⁰ С у кремнії.