Практические работы
16.1 Эмиссионный оптический анализ
Задача: в стали состава 4Х5Н2Т определить содержание хрома и никеля в феррите и аустените после закалки от t = 850оС с охлаждением в масло и низкотемпературного отпуска при t = 220оС.
По данным металлографического анализа структура стали - ≈30% феррита и 70% аустенита.
После травления в 5% реактиве азотной и серной кислоты на поверхности шлифа выявлен рельеф. Реактив растворяет аустенит, и поверхность обогащается ферритом.
Таким образом, следует методом оптического эмиссионного анализа определить содержание хрома и никеля в феррите и последующим расчётом определить содержание легирующих компонентов в аустените.
Расчёт содержание хрома в феррите и аустените:
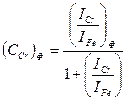 ·100% (1)
·100% (1)
ICr = 0,01; IFe = 0,6
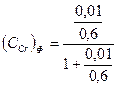 ·100 = 0,02·100 = 2%
·100 = 0,02·100 = 2%
Содержание хрома в феррите равно 2%.
Учитывая содержание феррита и аустенита в составе стали примем, что масса феррита равна 0,3, аустенита 0,7 условных единиц массы.
Обозначим условную. Единицу массы феррита 0.3 – α.

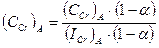 . (2)
. (2)
(ICr)A = 0,8; (1 – α) = 1 – 0,3 = 0,7
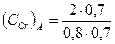 = 2,5%
= 2,5%
Содержание хрома в аустените равно 2,5%
Общее содержание хрома в феррите и аустените составляет 4,55%.
Расчёт содержания никеля в феррите и аустените.
Используем формулы (1) и (2).
(INi)Ф =0,02; IFe = 0,8
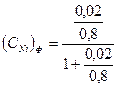 ·100 = 0,02·100 = 2%
·100 = 0,02·100 = 2%
Содержание никеля в феррите 2%.
(INi)A = 1,8
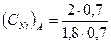 ·100 = 1,11%
·100 = 1,11%
Таким образом, общее содержание никеля в феррите и аустените составляет 3,11%.
16.2 Рентгеноспектральный флуоресцентный анализ
1. Расчёт необходимого количества образца для анализа.
При толщине излучающего слоя d, см, площадь образца, в котором вторичное излучение попадает на кристалл-анализатор равна S, см2, плотность анализируемого образца ρ, г/см3. Необходимое количество образца «Р» для элементного анализа, участвующего в формировании регистрируемой интенсивности аналитической линии рассчитывается по формуле:
P = dSρ.
Примем следующие значения:
S = 7,85 см; d1 =10-4 см; d2 = 10-2 см; ρFe = 7,88 г/см3
Р1 = 10-4·7,85·7,88 = 61,86·10-4 =618,6·10-3 г
Р2 = 10-2·7,85·7,88 = 61,86·10-2 г
2. Расчёт содержания никеля в стали
Расчёт проводится по наиболее сильной линии никеля λ1 К-серии.
Используется рентгеновская трубка с вольфрамовым зеркалом анода со сплошным первичным спектром.
Расчёт проводится по формуле:

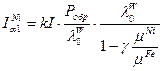 , (1)
, (1)
где 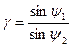 .
.
ψ1 = 73о – угол падения первичного рентгеновского излучения на образец;
ψ2 = 17о – угол выхода вторичного излучения.
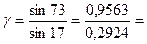 3,27
3,27
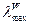 = 0,02138 нм - длина волны излучения рентгеновской трубки,
= 0,02138 нм - длина волны излучения рентгеновской трубки,
соответствующего максимальной интенсивности;
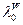 = 0,01178 – край спектра поглощения;
= 0,01178 – край спектра поглощения;
μNi = 1990 см3/г – массовый коэффициент ослабления первичного рентгеновского излучения в определённом элементе;
μFe = 2065 см3/г – массовый коэффициент ослабления в основном компоненте сплава.
Расчёт коэффициента k проводится по формуле:
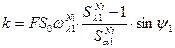 (2)
(2)
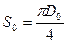 , D = 20 мм - диаметр образца.
, D = 20 мм - диаметр образца. 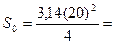 314 мм2
314 мм2
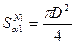 , D = 12 мм - площадь образца, на которую воздействует первичное рентгеновское излучение.
, D = 12 мм - площадь образца, на которую воздействует первичное рентгеновское излучение.
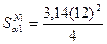 = 113,04 мм2
= 113,04 мм2
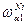 = кантовый выход для К-серии рассчитывается по формуле Стефенсона.
= кантовый выход для К-серии рассчитывается по формуле Стефенсона.
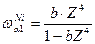 . (3)
. (3)
где b = 1,127·10-6 для рентгеновской трубки с W анодом;
Z = 74 – атомный вес вольфрама.
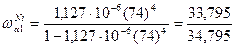 = 0,97
= 0,97
Iλ – полная интенсивность рентгеновской трубки со сплошным спектром рассчитывается по формуле:
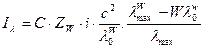 , (4)
, (4)
где С = 5·10-25 Дж/сек-2 - энергия импульса рентгеновского кванта;
i = 0,48 А/см2 - плотность тока рентгеновской трубки при напряжении
30 кВ;
с = 3·108 м/с - скорость квантов электромагнитного излучения.
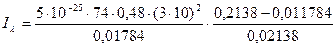 = 1523139·10-3 имп/с
= 1523139·10-3 имп/с
F - коэффициент, определяющий отражательную способность атомов никеля, рассчитывается по формуле:
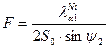 , (5)
, (5)
где 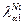 = 0,16579 нм - длина волны аналитической линии λα1 К-серии
= 0,16579 нм - длина волны аналитической линии λα1 К-серии
при определении содержания никеля.
S0 = ρ·d – поверхностная плотность образца: ρ = 7,86 г/см3 – плотность
материала образца;
d = 5 мм = 0,5 см – толщина образца.
S0 = 7,86·0,5 = 3,93 г/см3
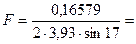 0,07
0,07
По формуле (2) рассчитаем коэффициент k.
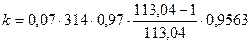 = 20,2
= 20,2
По формуле (1) рассчитаем интенсивность аналитической линии никеля:
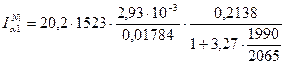 = 67683·10-3 имп/с
= 67683·10-3 имп/с
Таким образом, содержание никеля можно оценить из отношения:
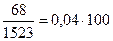 =4%
=4%
16.3 Дифракционная электронная микроскопия
Задача 1
16.3.1 Определение габитусной плоскости мартенситного кристалла
Фольги стали 25НЗЗ, деформирована при температуре -196°С (температура жидкого азота). Образец развернули в микроскопе так, что направление границы аустенитного и мартенситного кристаллов стало параллельным проекции оси наклона гониометрического столика на изображении, при данном увеличении.
Увеличения на двух снимках, снятых при разных наклонах образца (Δβ = 22°3'), различаются не более чем на 2% и этим различием можно пренебречь.
Ширина изображения границы на первом снимке оказалась равной 3,2 мм, на втором - 8 мм.
Применяя формулу:
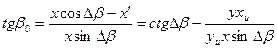 , (1)
, (1)
где β0 - начальный угол, который образует с плоскостью (001) радиус вращения точки с координатами хуz вокруг оси [010]. Рисунок 1.
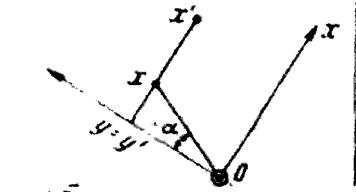
Рисунок 1. Расположение взаимного расположения
точек на изображении в результате наклона образца
при неизменном напряжении
Учитывая, что у - у' получим:
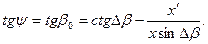
2,414- 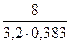 = -4,1
= -4,1
Знак тангенса показывает, что угол β0 отсчитывается от направления +х, больше 90°, а полюс габитусной плоскости отстоит от оси z на угол 180 – β0 = 76°20' с направлением + х. Рисунок 2.
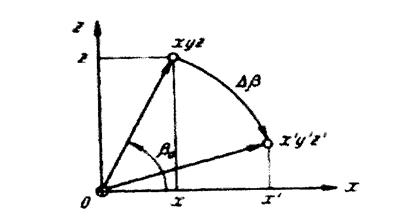
Рисунок 2. Изменение координат х и у точки xyz
при наклоне образца на угол Δβ
Измерениями на полученном изображении с использованием стереографической проекции, уточнены ориентировки аустениного и мартенситного кристаллов, а их ориентационные соотношения и определены атомных плоскостей. Индексы искомой габитусной плоскости мартенситного кристалла получаются:
h : k: l = 0,242 : 0,749 : 0,616 ≈ 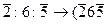 )
)
На рисунке 3 показана область, в пределах которой может в действительности находиться полюс «Г».
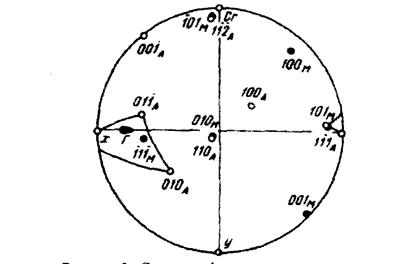
Рисунок 3. Стереографическая проекция
Ось зоны проекции антипараллена первичному электронному пучку. Оси х и y вспомогательной системы координат, направление следа габитусной плоскости мартенситного кристалла СГ и найденный полюс габитусной плоскости «Г».
Задача 2
16.3.2 Определение плоскости дефекта упаковки,
наклона и толщины фольги
Получены снимки участка образца аустенитной стали с низкой энергией дефекта упаковки. Второй снимок сделан при наклоне гонеометрического столика с образцом на угол Δβ = +26°48 . С учётом взаимного разворота дифракционных картин при данном увеличении (13000) найдено направление на снимках проекции оси наклона.
Начало вспомогательной системы координат выбрано в вершине угла дефекта упаковки. Перпендикулярно оси у проведена ось х , отстоящая от оси «х» на 18 мм. Линия 1 и восьми (включая нулевую) точках пересекают следы двух дефектов упаковки. Координаты этих точек хi, у i, х’I, у’i
измеренные на снимках при увеличении 130000, а также zi, вычисленные по формуле (1), приведены на рисунке 3 и в таблице 1.
По полученным координатам построены сечения фольги в проекции на плоскость (010) и (001). На рисунке 3 приводится графическое построение для определения следа дефекта упаковки на плоскости (001) и измерения угла β0 наклона дефекта к этой плоскости. Измерение угла даёт значение β0 = 28,5о.
На стереографической проекции для оси зоны, близкой к [110] и с уточнением по сильным рефлексам на электроннограмме положением полюса (110). Показаны направления осей x и y следа дефекта упаковки СГ и полюс «Г» искомой плоскости дефекта.
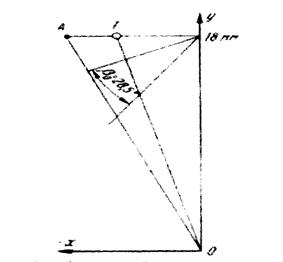
Рисунок 3. Графическое изображение определения
положения дефекта упаковки в проекции на плоскость
(001): ОА - след дефекта упаковки на плоскость
(001); 01-проекция следа на верхней поверхности фольги
Таблица 1.
| Номер точки | На снимке «а» | На снимке «б» | Расчёт для снимка «а» | ||
| х | y | x’ | y’ | Z | |
| -5,0 | -4,6 | +1,5 | |||
| -20,4 | -13,6 | -6,5 | |||
| -22,1 | -20,5 | +7,2 | |||
| -37,0 | -29,5 | ||||
| -15,6 | -9,3 | -7,8 | |||
| -17,5 | -16,2 | +5,7 | |||
| -33,1 | -25,9 | -1,1 |
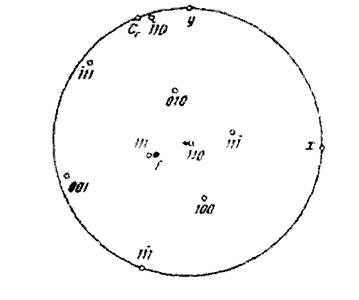
Рисунок 4. Стереографическая проекция.
Ось зоны антипараллена направлению первичного пучка и отклонена от направления [110] примерно на 4°.
Найденная плоскость на 3,5° отстоит от (111), в которой лежат дефекты упаковки в г. ц. к. кристаллах.
Поскольку фольга не изогнута вокруг оси «х» можно прямо измерять (с учётом увеличения на снимке и на чертеже) толщину фольги и угол наклона
фольги к (001).
Измерения и расчёт дают t = 93,0 нм и угол ν = 18°. Несложными графическими построениями можно найти и истинное расстояние между дефектами.
Таким образом, после аналитического определения координат точек практически все дальнейшие операции кристаллографической привязки структурных особенностей и различные пространственные измерения можно провести не только аналитически, но и графически.
16.4 Микрорентгеноспектральный анализ
Анализ с использованием гиперболического метода
Гиперболический, или эмпирический метод, используется для содержания элементов в бинарной системе. Используется уравнение:
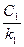 = a1.2 + (1 – a1.2)·C1, (1)
= a1.2 + (1 – a1.2)·C1, (1)
где С1 - концентрация первого элемента (1) в бинарной системе, состоящей из элементов 1 и 2;
k1 - отношение интенсивностей излучения от элемента (1) в образце и эталоне после введения поправок на фон и мёртвое время регистрации рентгеновского излучения;
а1.2 - коэффициент а1.2 для определения элемента (1) в бинарной состоящей из элементов 1 и 2.
Из выражения (1) следует, что коэффициент а1.2 может быть определён при условии, что С1 стремится к нулю.
Поправочный коэффициент для многокомпонентной системы элементов может быть выражен для n-го элемента уравнениями:
Cn = knβn (2)
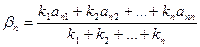 . (3)
. (3)
В уравнении (3): аn1 - значение коэффициента «а» для определения элемента n в бинарной системе, состоящей из элементов n и 1;
nn2 – значение «а» для определения элемента n в бинарной системе, состоящей из элементов n и 2 и т.д. до ann, который равен 1.
Таким образом, обозначение a1n представляет значение «а» для определения элемента 1 в бинарной системе, состоящей из элементов n и 1.
k1, k2 … kn - представляют отношение измеренных рентгеновских интенсивностей излучения от элемента 1, 2,.... п в образце к соответствующим интенсивностям от эталонов для этих же элементов.
Для вычисления конечного значения Сn рассчитывается совокупность значений βn до тех пор, пока разности результатов последовательных расчётов не станут произвольно малыми. Обычно необходимо не более трёх- четырёх вычислений. Основное условие применения гиперболического метода - это располагать соответствующую совокупность значений «а», которая определена для многих элементов и приводится в справочных таблицах.
Для расчёта содержания элементов в образцах составляется матрица. Для четырёхкомпонентной системы необходимая матрица значений имеет вид:
а11 = 1 а12 а13 а14
а21 а22 = 1 а23 а24
а31 а32 а33 = 1 а34
а41 а42 а43 а44 = 1
Для вычисления необходимых значений β выбирается соответствующая совокупность значений «а» и вычисление производится по выражению:
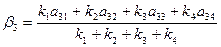


В вычислительной схеме задаются значением «С» и вычисляют соответствующие значения k и а. Преимущество методики состоит в том, что в случае, когда известен качественный состав образца и производится его количественный анализ, матрицу значений «а» можно получить расчётным путём. При этом необходимо выполнения следующих условий:
- получать и хранить поступающие от счётчиков данные интенсивности
излучения от анализируемого объекта, эталонов и фона, а также время анализа;
- подставить полученную от счётчиков информацию в имп/с;
- ввести поправку на мёртвое время в полученные данные по скорости
счёта импульсов;
- соответственно вычесть величину фона;
- обработать статистические данные по выбранной методике.
- вычислить значения k1, k2,… kn;
- найти соответствующие значения «а» по матрице;
- вычислить β1, β2 … βn по уравнению (3);
- определить С1, С2 … Сn по уравнению (2);
- повторить процесс вычислений до получения сходимости результатов вычислений β и С.
Эти расчёты можно выполнить на калькуляторе с программным управлением, при этом время, необходимое для обработки результатов одного измерения, в случае шестикомпонентной системы составляет около 3 минут.
Соответствующую а-матрицу вручную, если не требуется введения поправки на эффект вторичной флуоресценции, или с большими затратами времени, когда такие поправки необходимы. Для этой цели используется выражения:
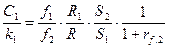 . (4)
. (4)
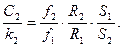 (5)
(5)
Значения r могут быть сгруппированы попарно следующим образом:
R’f.1 = 0 R’f.2 = 0
R’f.1 > 0 R’f.2 = 0 (6)
R’f.1 = 0 R’f3 > 0
Необходимые значения R могут вычислены по выражению U = 10 кВ:
R = R’1 – R’2 lg(R3’Z + 25) (7)
R’1 = 8,73·10-3 U3 – 0,1669U2 +0,9662U + 0,4523 = 2,15
R’2 = 2,703·10-3U3 – 5,182·10-2U2 + 0,302U +0,1836 = 0,357
R’3 = (0,88U3 – 3,44U2 +9,33U -6,43)U3 = 0,629
Значения тормозной способности S могут быть получены из соотношения:
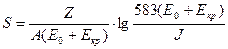 . (8)
. (8)
В справочной таблице приведены значения величины отношения 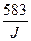 . В выражении (8) значения Е0 и Екр выражаются в киловольтах, J – в электрон-вольтах.
. В выражении (8) значения Е0 и Екр выражаются в киловольтах, J – в электрон-вольтах.
Фактор поглощения f вычисляется при условии, что U или χ, либо то и другое, малы, удовлетворительный результат даёт выражение:
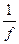 = 1 + 3·10-6 (Е01,65 – Екр1,56). (9)
= 1 + 3·10-6 (Е01,65 – Екр1,56). (9)
Для изучаемого объекта из n элементов необходимо получить n(n – 1) значений для «а», n, значений для U, для Екр и по n2 значений для R, S, f и 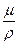 .
.
Расчёт содержания Mo и W в образце по данным микрозондового анализа. Используются справочные и экспериментальные данные, необходимые для расчёта. Таблица 1.
Операции вычисления.
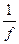 = 1 + 3·10-6 (Е01,65 – Eкр1,65)χ + 4,5·10-13 (E01,65 – Eкр1,65)2χ2
= 1 + 3·10-6 (Е01,65 – Eкр1,65)χ + 4,5·10-13 (E01,65 – Eкр1,65)2χ2
Таблица 1. Значения параметров для определения Mo и W
| Mo | W |
Екр = 2,525 кэВ
U = 7,92 кВ
M(W, MoLα) = 728
M(W, MoLα) = 3145
χ1 = 918
χ2 = 3964
Z = 42
A = 95,94
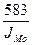 = 1,329 = 1,329
| Екр = 10,2 кэВ
U = 1,96 кВ
M(W, WLα = 151
M(Mo, WLα) = 140
χ1 = 176,5
χ2 = 190,3
Z = 74
A = 183,85
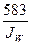 = 0,779 = 0,779
|
Расчёт для определения содержания Mo.
Расчёт поправки на поглощение рентгеновского излучения.
Е01.65 – Екр1.65 = 135,6
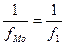 = 1,318, f1 =0,724
= 1,318, f1 =0,724
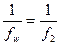 = 2,743, f2 = 0,365
= 2,743, f2 = 0,365
Расчёт тормозной способности.
Е0 – Екр = 22,525
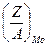 = 0,4377,
= 0,4377, 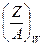 = 0,4025
= 0,4025
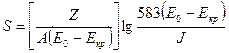
S1 = SMo = 0,00660
S2 = SW = 0.0512
Фактор обратного рассеяния при U = 7,92, по табличным данным.
R’1 = 1,97, R’2 = 0,30, R’3 = 0,585
R1 = RMo = 0,798
R2 = RW = 0,702
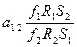 = 1,749
= 1,749
Расчёт для W
Расчёт поправки на поглощение.
Е01,65 – Екр1.65 = 140,2 - 46,2 = 94
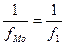 = 1,050, f1 = 0,952
= 1,050, f1 = 0,952
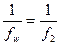 = 1,054, f2 = 0,949
= 1,054, f2 = 0,949
Тормозная способность.
Е0 - Екр = 30,2
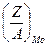 = 0,4377;
= 0,4377; 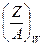 = 0.4025
= 0.4025
S1 = SMo = 0,0535
S2 = SW = 0,421
Фактор обратного рассеяния при U = 1,96 по табличным данным.
R’1 = 1,76
R’2 = 0,228
R’3 = 0,706
R1 = RMo = 0,848; R2 = RW = 0,769.
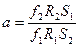 = 1,149
= 1,149
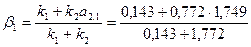 = 1,632
= 1,632
C’1 =C’W = 0,772·1,023 = 0,790
Расчёт содержания Mo и W.
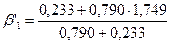 = 1,578
= 1,578
C’’1 = 1,578·0,143 = 0,226
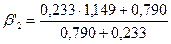 = 1,034
= 1,034
C’’2 = 0,798
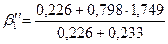 = 1,584
= 1,584
CMo = 1,584·0,143 = 0,226%
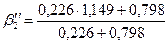 = 1,033
= 1,033
CW = 0,797%
16.5 Рентгеноструктурный анализ
16.5.1.Фазовый анализ по данным о межплоскостных расстояниях
Основой расчёта является уравнение Брега:
nλ = 2sinθ, (1)
которое преобразуется к виду:
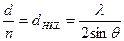 , (2)
, (2)
где λ – длина волны рентгеновского характеристического излучения, которая определяется типом используемой рентгеновской трубки;
dHKL – межплоскостные расстояния кристаллической решётки поликристаллического материала.
θ – дифракционный угол рентгеновского отражения зафиксированного на дифрактограмме во всём диапазоне дифракционных углов, где могут находится отражения от фаз входящих в состав сталей.
Поликристаллические материалы: металлы, сплавы, интерметаллиды, соединения металлов с азотом, углеродом и другие соединения и сложные металлические и неметаллические соединения, каждое из которых имеет свою кристаллическую решётку со строго определёнными межплоскостными расстояниями. Это является основой проведения рентгеноструктурного фазового анализа.
Таким образом, (2) для определения межплоскостных расстояний dHKL необходимо определить дифракционный угол θ. Длина волны рентгеновского характеристического излучения известна для каждой трубки.
Практическая часть
1. По дифрактограмме выписать дифракционные углы 2θ (по отметчику углов)
2. По справочным таблицам определить значение dHKL по углу θ.
3. Построить штрих диаграммы в единицах dHKL
4. В таком же масштабе построить штрих-диаграммы от предполагаемых фаз, входящих в состав материала.
5. Индексы (HKL) проставить используя справочные таблицы
Данные для расчёта.
Использовалась рентгеновская трубка с железным зеркалом анода.
Длина волны λКα1 = 1,93597Ǻ
λКα2 = 1,93991 Ǻ
Средне взвешанная длина волны 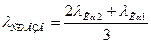 = 1,93728 Ǻ
= 1,93728 Ǻ
На рисунке 1 приводится построенная штрих диаграмма в единицах d (HKL). На рисунках 2 и 3 приводится штрих-диаграмма от предполагаемых фаз, входящих в состав стали.

Рисунок 1. Штрих-диаграмма, построенная
по записанной на дифрактометре
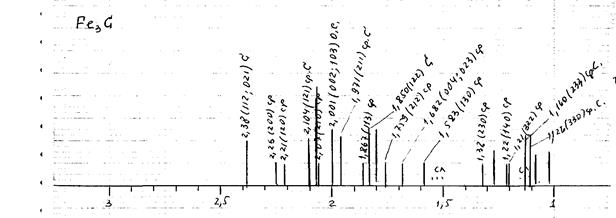
Рисунок 2. Штрих-диаграмма цементита
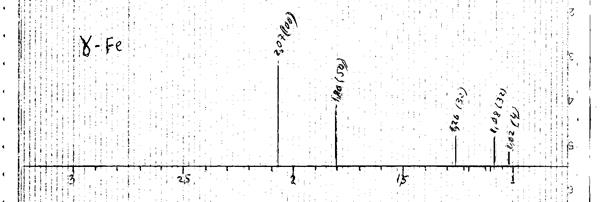
Рисунок 3. Штрих-диаграмма аустента
Таким образом, в состав стали входят две фазы - цементит Fe3C и аустенит γ-Fe.
16.5.2. Расчёт параметра кристаллической решётки для
кубической сингонии
Первый метод расчёта
Расчёт проводится по формуле:
а = dHKL 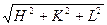 (1)
(1)
Первый метод расчёта.
1. Используются дифракционные отражения под углом отражения
θ > 60о
2. Использовать отражения от феррита с индексами интерференции, которые определяются по справочной таблице и соответствующие этим линиям индексы интерференции – операция индицирования.
3. Рассчитать ошибку в определении параметра кристаллической решётки по формуле:
∆а = аctgθ∆θ (2)
Используется дифракционное отражение от феррита с индексами интерференции (220) с межплоскостным расстоянием dHKL = 1,03 и дифракционным углом отражения θ = 70,12о.
а = 1,03· 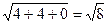 = 1,03·2,828 = 3,68 = 0,368 нм
= 1,03·2,828 = 3,68 = 0,368 нм
Табличное значение параметра кристаллической решётки феррита а = 0,287 нм. Увеличенный параметр связан с растворением легирующих элементов в феррите. Использовалась сталь 45ХМ после нормализации.
Δa = 0,368·ctg70,12·0,14 = 0,368·1/tg70,12·(0,14) = 0,368·0,36·0,14 = 0,02
Второй метод расчёта.
1. Используется дифракционное отражение под углом θ > 70о.
2. Разбиваем большеугловое отражение на n равных частей.
3. Определяем дифракционные углы для двух крайних значений n.
4. Определяется центр тяжести одного дифракционного отражения по формуле, рисунок 4:
2θц.т = 2θх=0 + хц.т. 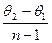
5. Расчёт проводится по формуле: а = 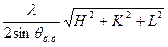
6. Ошибка рассчитывается по формуле (2)
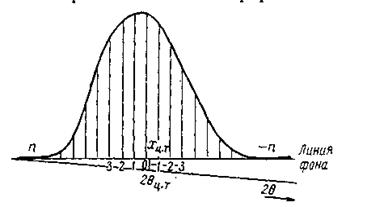
Рисунок 4. К определению центра тяжести дифракционной линии
2θЦ.Т. = 2·70,12 + 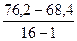 = 140,24 + 0,52 = 141,28
= 140,24 + 0,52 = 141,28
θЦ.Т = 70,64о
а = 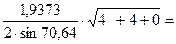 2,983·1,03 = 3,06 Ǻ = 0,306 нм
2,983·1,03 = 3,06 Ǻ = 0,306 нм
Таким образом, по второму методу расчёта параметр элементарной ячейки определяется более точно и равен 0.306 нм. При этом параметр остаются увеличенным по сравнению с табличным значением.
Третий метод расчёта.
1. Используется три-четыре дифракционных отражения под углом
θ > 40о.
2. Проводится расчёт параметра кристаллической решётки по формуле (1) для всех дифракционных отражений.
3. Строится график зависимости в координатах а - 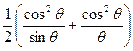 .
.
4. Проводится экстраполяция до пересечения с ординатой, которая принимается за значение параметра кристаллической решётки. Рисунок 5.
Расчёт параметра кристаллической решётки феррита проводится по формуле:
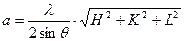
a1 = 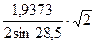 = 2,91 Ǻ; a2 =
= 2,91 Ǻ; a2 = 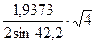 = 2,89 Ǻ;
= 2,89 Ǻ;
a3 = 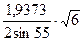 = 2,89 Ǻ; a4 =
= 2,89 Ǻ; a4 =  = 3,11 Ǻ
= 3,11 Ǻ 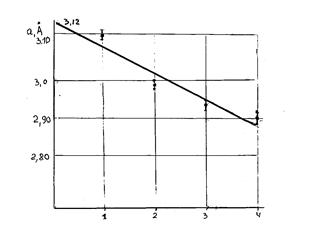
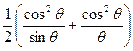
Таким образом, по расчётам параметра кристаллической решётки феррита получены значения:
первый метод а = 0,368 нм
второй метод а = 0,306 нм
третий метод а = 0,312 нм
16.5.3 Определение микродеформаций и областей когерентного
рассеяния методом аппроксимации
Под микронапряжениями понимают напряжения, которые уравновешиваются в объёме отдельных кристаллитов металлов, расчёт основан на представлении о том, что они связаны с неоднородной упругой деформацией кристаллитов и, вследствие этого, с изменением межплоскостных расстояний в кристаллической решётке.
При наличии микронапряжений каждая система атомных плоскостей с одинаковыми индексами интерференции (hkl) имеет вместо строго определённого межплоскостного расстояний dhkl межплоскостное расстояние d + Δd.
Величина микронапряжений оценивается по величине относительной деформации кристаллической решётки металлов: 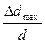 . Для кристаллов кубической сингонии:
. Для кристаллов кубической сингонии:
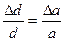 . (1)
. (1)
Значения d + dmax и дифракционные углы θ для каждой системы атомных плоскостей будут находиться в интервале значений θ + Δθmax , что приводит к расширению рентгеновских отражений и тем большему, чем больше будут значения ±d и Δθ.
Эффект расширения линий на дифрактограмме вызывают также дисперсность кристаллических блоков (ОКР). На ширину линий влияет расходимость первичного рентгеновского характеристического излучения, поглощение материалом образца, расположение и размеры осветительных и аналитических диафрагм - геометрический фактор, наложение или неполное разделение α1-α2 дуплета.
Для последующего расчёта структурных характеристик металлов примем следующие обозначения:
В'- экспериментальная общая ширина максимума от изучаемого образца;
в'- тоже для эталона;
В - истинная ширина отражения от образца;
в - истинное геометрическое уширение линии эталона;
β - истинное физическое уширение линии от образца;
n - часть истинного физического уширения линии, вызванной наличием микронапряжений в образце;
m - часть истинного уширения линии, вызванной дисперсностью кристаллических блоков;
Δа/а - относительная микродеформация кристаллической решётки;
Dhkl - величина блоков когерентного рассеяния.
Если известно физическое состояние образца, из которого можно заключить, что физическое уширение линии (hkl) вызвано исключительно наличием микронапряжений или только дисперсностью блоков когерентного рассеяние (меньше 0,1 мкм), то величина искажений решётки в направлении перпендикулярном плоскости отражения (hkl) и размер кристаллических блоков, рассчитываются по простым формулам:
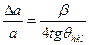 - величина кристаллических блоков. (2)
- величина кристаллических блоков. (2)
Dhkl = 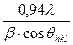 - величина кристаллических блоков. (3)
- величина кристаллических блоков. (3)
В большинстве случаев в изучаемых металлических сплавах уширение дифракционных отражений вызвано, кроме геометрических факторов наличием микронапряжений и дисперсностью кристаллических блоков. В этом случае расчет по формулам (2) и (3) возможен только после выделения факторов m и n в физическом уширении каждого выбранного дифракционного максимума.
Анализ распределения интенсивности в рентгеновском отражении даёт возможность установить, что величина В - истинное уширение линии, свободное от наложения дуплета α1-α2 связана с физическим уширением линии и b - истинное геометрическое уширение эталона свободное от наложения дуплета, определяются выражением:
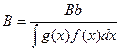 . (3)
. (3)
Функции g(х) и f(х) определяют угловое распределение интенсивности дифракционного отражения из-за одновременного воздействия геометрии съёмки, наличия микронапряжений и дисперсности областей когерентного рассеяния. Эти функции аппроксимируются различными выражениями, которые с различной степенью точности описывают распределение интенсивности в рентгеновских отражениях. Для металлов с кубическими решётками Бравэ результаты достаточно большой точности даёт аппроксимация по выражению:
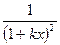 . (4)
. (4)
При известной аппроксимирующей функции истинное физическое уширение определяется при съёмке на дифрактометре двух максимумов от изучаемого образца и эталона. Одна из линий имеет небольшой угол отражения с небольшой суммой квадратов индексов интерференции, второй максимум записывается с максимально возможным углом отражения с большой суммой квадратов индексов Миллера, аналогичные максимумы записываются от образца-эталона.
Выбор отражений под малыми и большими углами связан преимущественным влияниям размеров кристаллических блоков на линии с небольшими дифракционными углами. Наличие микронапряжений оказывает основное влияние на линии с большими углами отражения. Образцы, которые используются в качестве эталонов, не должны иметь микронапряжений, которые оцениваются по степени разрешения α1-α2-дуплета. Величина кристаллических блоков, не должна оказывать влияния на ширину отражений, которые должны определяться только геометрическим фактором.
Использование метода аппроксимации при расчёте величины микронапряжений и размеров кристаллических блоков, в большинстве случаев используются данные о полуширине рентгеновских отражений, за которую принимают расстояние между двумя точками, в которых интенсивность равна половине максимального значения. .
Находит применение измерение интегральной ширины - это ширина дифракционного профиля, выпрямленного до прямоугольника, причём его общая площадь и максимальная высота такие же, как у профиля экспериментального максимума, рисунок 1. Такой профиль получают, разделив общую площадь максимума на его максимальную ординату.
Определив полуширину дифракционных отражений, получают экспериментальное уширение изучаемого образца «В» и эталона b. Уширение выражают в радианах с учётом масштаба записи отражений, который определяется скоростью движения диаграммной ленты и регистрирующего потенциометра.
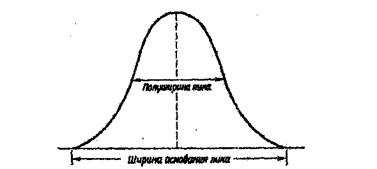
Рисунок 1. Метод измерения полуширины максимума
Экспериментальные общие уширения В и b, полученные при съёмке в характеристическом рентгеновском излучении, являются наложением дуплета α1–а2. Поэтому необходимо ввести поправку на дуплетность, которая рассчитывается по уравнению:
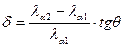 . (5)
. (5)
Схематически метод выделения из экспериментальной ширины рентгеновского максимума компоненты α1 приводится на рисунке 2 (метод Решингера).
Для получения значений ширины отражений от изучаемого образца и эталона используется поправочный график, на котором приводятся значение 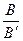 взависимости от
взависимости от 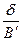 . Рисунок 2.
. Рисунок 2.
Экстропаляционная функция выбирается в зависимости от формы профиля дифракционных отражений. Рисунок 3.
По исправленным на дублетность максимумов находят физическое уширение β  . Аппроксимация уравнения (3) через функции:
. Аппроксимация уравнения (3) через функции:
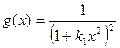 ;
; 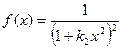 , (6)
, (6)
приводит к уравнению:
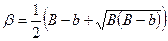 (7)
(7)
Уравнение (7) графически представляют в виде зависимости 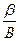 от
от 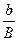 , которая приводится на рисунке 4. По этим графикам определяют значение физического фактора уширения дифракционных отражений под небольшим углом и максимально большим дифракционным углом.
, которая приводится на рисунке 4. По этим графикам определяют значение физического фактора уширения дифракционных отражений под небольшим углом и максимально большим дифракционным углом.
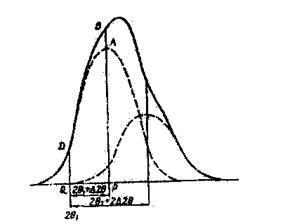
Рисунок 2. Схема введения поправки на
дублетность дифракционного отражения
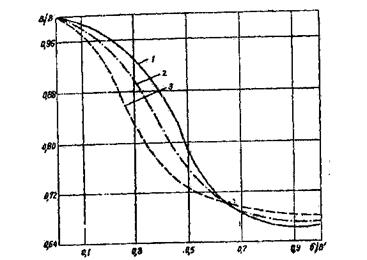
Рисунок 3. График поправок на α1-α2 дублет
1 - 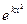 ; 2 -
; 2 - 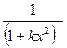 ; 3 -
; 3 - 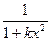
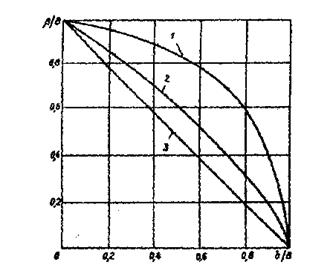
Рисунок 4. График поправок для выделения физического
фактора уширения: 1 - 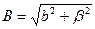 ; 2 -
; 2 - 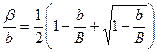 ;
;
3 - B = b + β
После выделения физического фактора уширения рентгеновских максимумов следует провести оценку доли влияния дисперсности кристаллических блоков и наличия микронапряжений.
В случае, если ОКР крупнее 0,1 мкм, то физическое уширение вызвано только микронапряжениями, тогда из формулы (2):
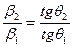 , (8)
, (8)
из которой следует, что уширение пропорционально tgθ_.
В случае, если в образце нет микронапряжений, но ОКР меньше 0,1 мкм, то физическое уширение вызвано только дисперсносностью кристаллических блоков (ОКР), тогда из формулы (3) следует:
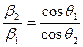 , (9)
, (9)
из которой следует, что уширение обратно пропорционально cosθ.
В большинстве случаев, в металлических сплавах уширение рентгеновских максимумов вызвано обоими факторами: микронапряжениями и дисперсностью кристаллических блоков. В этом случае из физического фактора уширения нужно выделить m - уширение вызванное малостью ОКР и n - уширение, вызванное наличием микронапряжений. Для этой цели используется выражение:
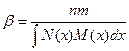 , (10)
, (10)
где М(х) - функция наличия микронапряжений; N(х) - функция, определяющая дисперсность кристаллических блоков. Аппроксимация выражения (10) через функции:
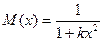 и
и 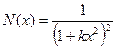 , (11)
, (11)
приводят к отношению:
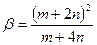 . (12)
. (12)
Уравнение (12) с двумя неизвестными неразрешимо, поэтому необходимо использовать две линии дифрактограммы, для которых физические факторы уширения будут равны:
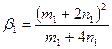 ;
; 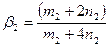 . (13)
. (13)
В соответствие с формулами (2) и (3) получим уравнения:
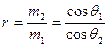 и
и 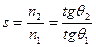 . (14)
. (14)
Решая уравнения (2) и (3) совместно, находим отношения: 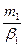 и
и 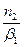 .
.
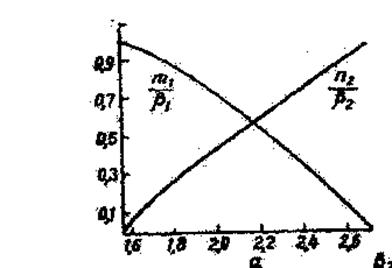
Строим трафики зависимости: 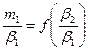 и
и 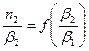 . Рисунок 5.
. Рисунок 5.
Дата добавления: 2020-07-18; просмотров: 625;











