Схема реализации оптимального некогерентного приёма

;

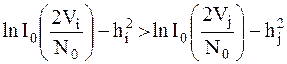(2.1)

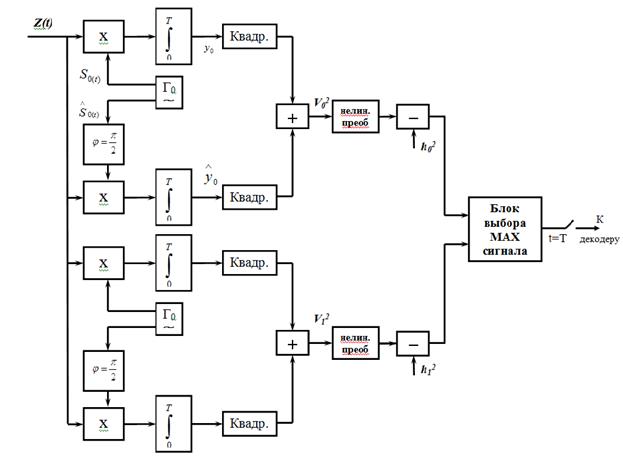
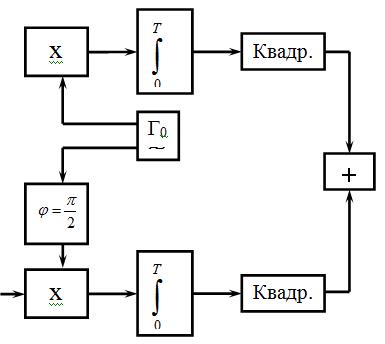
Схема, реализующая данную процедуру, получила название квадратурная. В ней выполняются практически все указанные выше операции в процессе приема сигналов. Ее вид для двоичной системы ЧМ сигналов представлен на рис.1

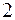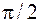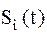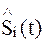
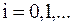Приемник содержащий ветви (по числу реализующей сигнала). С помощью генераторов и фазовращателей на (преобразователи Гильберта) формируются синфазные и квадратурные компоненты и которые поступают на перемножители, на другие входы которых подается колебание 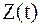. После перемножения и интегрирования формируются величины 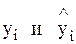. Далее из них получается значение 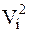, которые после нелинейного безынерционного преобразования с характеристикой

;

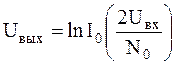(2.2)

подаются на пороговые устройства, где у них вычисляется .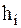

Рис.1 Оптимальный некогерентный приемник при неизвестной фазе сигнала

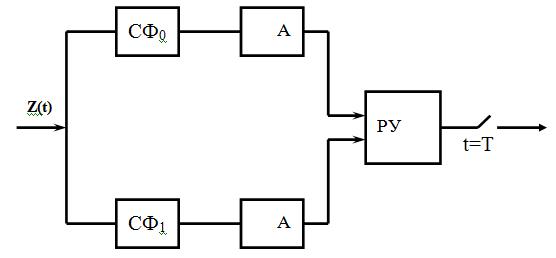
Схема оптимального приёмника (некогерентного) на СФ приведена на рис. 2. Эта схема содержит 2 СФ (для двоичных систем).

На выходе каждого СФ получается напряжение, пропорциональное функции взаимной корреляции:

;

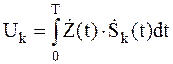(2.3)

Амплитудный детектор (АД) выделяет огибающую (модуль) этой функции. Затем производиться отсчёт и принимается решение.

Рис. 2. Структурная схема некогерентного приёмника двоичных сигналов на СФ.

;

;

;

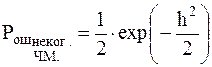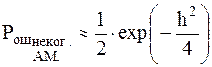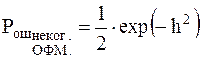При переходе от когерентного приёма к некогерентному проигрыш оказывается незначительным, причём с увеличением требований к верности приёма (с уменьшением 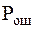) он уменьшается. В связи с этим, а также ввиду значительных сложностей получения опорных колебаний, синфазных с принимаемым сигналом, как правило, приходит к некогерентному приёму даже в тех случаях, когда фаза сигнала изменяется очень медленно.