Основные определения. Способы изображения деревьев

Определение: Деревом будем называть конечное множество T, состоящее из одного или более узлов, таких что:
а) Имеется один специальный узел, называемый корнем данного дерева.
б) Остальные узлы (исключая корень) содержатся в 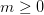попарно непересекающихся подмножествах , каждое из которых в свою очередь является деревом. Деревья называются поддеревьями данного дерева.

Это определение является рекурсивным. Если коротко, то дерево это множество, состоящее из корня и присоединенных к нему поддеревьев, которые тоже являются деревьями. Дерево определяется через само себя. Однако данное определение осмысленно, так как рекурсия конечна. Каждое поддерево содержит меньше узлов, чем содержащее его дерево. В конце концов, мы приходим к поддеревьям, содержащим всего один узел, а это уже понятно, что такое.

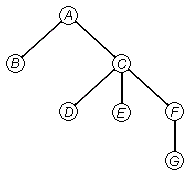
Рис. 3. Дерево.

На рис. 3 показано дерево с семью узлами. Хотя обычные деревья растут снизу вверх, рисовать их принято наоборот. При рисовании схемы от руки такой способ, очевидно, удобнее. Из-за данной несогласованности иногда возникает путаница, когда говорят о том, что один из узлов находится над или под другим. По этой причине удобнее пользоваться терминологией, употребляемой при описании генеалогических деревьев, называя более близкие к корню узлы предками, а более далекие потомками.

Узлы, не содержащие поддеревьев, называются концевыми узлами или листьями. Множество не пересекающихся деревьев называется лесом. Например, лес образуют поддеревья, исходящие из одного узла.

Графически дерево можно изобразить и некоторыми другими способами. Некоторые из них представлены на рис. 4. Согласно определению дерево представляет собой систему вложенных множеств, где эти множества или не пересекаются или полностью содержатся одно в другом. Такие множества можно изобразить как области на плоскости (рис. 4а). На рис. 4б вложенные множества располагаются не на плоскости, а вытянуты в одну линию. Рис. 4б также можно рассматривать как схему некоторой алгебраической формулы, содержащей вложенные скобки. Рис. 4в дает еще один популярный способ изображения древовидной структуры в виде уступчатого списка.

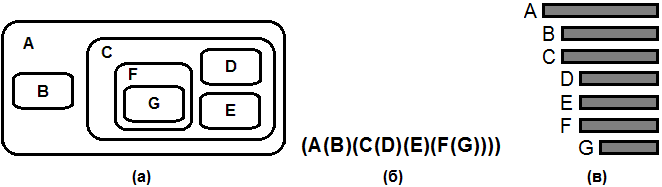
Рис. 4. Другие способы изображения древовидных структур: (а) вложенные множества; (б) вложенные скобки; (в) уступчатый список.

Уступчатый список имеет очевидное сходство со способом форматирования программного кода. Действительно, программа, написанная в рамках парадигмы структурного программирования, может быть представлена как дерево, состоящее из вложенных друг в друга конструкций.

Также можно провести аналогию между уступчатым списком и внешним видом оглавлений в книгах, где разделы содержат подразделы, те в свою очередь поподразделы и т.д. Традиционный способ нумерации таких разделов (раздел 1, подразделы 1.1 и 1.2, подподраздел 1.1.2 и т.п.) называется десятичной системой Дьюи. В применении к дереву на рис. 3 и 4 эта система даст:

1. A; 1.1 B; 1.2 C; 1.2.1 D; 1.2.2 E; 1.2.3 F; 1.2.3.1 G;