Синтаксический анализ арифметических выражений

Задача синтаксического анализа заключается в том, чтобы по имеющейся строке, содержащей арифметическое выражение, и известным значениям, входящих в нее переменных, вычислить значение выражения.

Процесс вычисления арифметических выражений можно представить в виде бинарного дерева. Действительно, каждый из арифметических операторов (+, –, *, /) требует двух операндов, которые также будут являться арифметическими выражениями и, соответственно могут рассматриваться как поддеревья. Рис. 8 показывает пример дерева, соответствующего выражению:

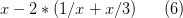
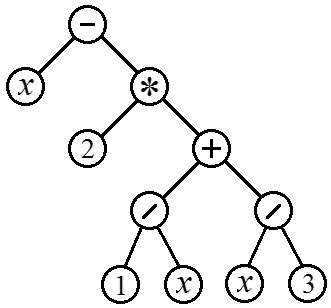
Рис. 8. Синтаксическое дерево, соответствующее арифметическому выражению (6).

В таком дереве концевыми узлами всегда будут переменные (здесь x) или числовые константы, а все внутренние узлы будут содержать арифметические операторы. Чтобы выполнить оператор, надо сначала вычислить его операнды. Таким образом, дерево на рисунке следует обходить в концевом порядке. Соответствующая последовательность узлов

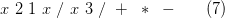
называется обратной польской записью арифметического выражения.

При построении синтаксического дерева следует обратить внимание на следующую особенность. Если есть, например, выражение

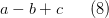
и операции сложения и вычитания мы будем считывать слева на право, то правильное синтаксическое дерево будет содержать минус вместо плюса (рис. 9а). По сути, это дерево соответствует выражению 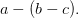Облегчить составление дерева можно, если анализировать выражение (8) наоборот, справа налево. В этом случае получается дерево с рис. 9б, эквивалентное дереву 8а, но не требующее замены знаков.

Аналогично справа налево нужно анализировать выражения, содержащие операторы умножения и деления.

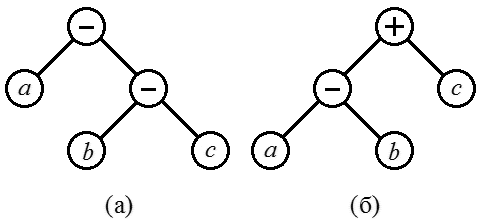
Рис. 9. Синтаксические деревья для выражения a – b + c при чтении слева направо (а) и справа налево (б).

В файле SynAn.pas приведен пример функции, вычисляющей значения выражений, содержащих только одну переменнуюx. Дадим краткое описание реализованного там алгоритма:

1. Вычисляющая выражение функция (CalcExpression) находит в строке все знаки «+» и «–», не заключенные в скобки. Эти знаки разбивают выражение на части, содержащие (вне скобок) только операции умножения и деления. Для вычисления значений этих частей вызывается функция CalcMultDiv.

2. Функция CalcMultDiv находит в строке все знаки «*» и «/», не заключенные в скобки. Эти знаки разбивают выражение на части, содержащие числовые константы, переменную x или выражения в скобках. Для вычисления значений этих частей вызывается функция CalcValuesOrOpenParentheses.

3. Функция CalcValuesOrOpenParentheses определяет тип попавшего ей на вход выражения. Если это числовая константа или переменная x, то она возвращает их значение. Если это выражение в скобках, то для его вычисления рекурсивно вызывается процедура CalcExpression.

Заметим, что в данном примере вычисления производятся одновременно с анализом строкового выражения. Это приводит к тому, что для некоторых выражений вычисления могут происходить в 100 – 1000 раз медленнее, чем, если бы эти выражения были скомпилированы как часть программы. Если одно и то же выражение требуется вычислить много раз при различных значения переменных, то следует разделить анализ строки и вычисления. Такой подход может позволить ускорить вычисления в сотни раз.

Результатом анализа строки должна быть последовательность узлов дерева в концевом порядке. Каждый узел должен хранить информацию о подузлах и о той операции, которая в нем совершается. Например, узлы можно реализовать в виде записей, одно из полей который имеет процедурный тип. Другой вариант – каждый узел это объект, где операция реализована как виртуальный метод.

Быстрые сортировки

Простые методы сортировки вроде метода выбора или метода пузырька сортируют массив из n элементов за O(n²) операций. Однако с помощью принципа «разделяй и властвуй» удается построить более быстрые, работающие за O(nlog₂ n) алгоритмы. Суть этого принципа в том, что решение получается путем рекурсивного разделения задачи на несколько простые подзадачи того же типа до тех пор, пока они не станут элементарными. Приведем в качестве примеров несколько быстрых алгоритмов такого рода.