Рекуррентные соотношения. Рекурсия и итерация
Говорят, что последовательность векторов 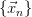 задана рекуррентным соотношением, если задан начальный вектор
задана рекуррентным соотношением, если задан начальный вектор 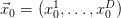 и функциональная зависимость последующего вектора от предыдущего
и функциональная зависимость последующего вектора от предыдущего
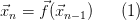
Простым примером величины, вычисляемой с помощью рекуррентных соотношений, является факториал
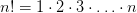
Очередной факториал 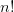 можно вычислить по предыдущему как:
можно вычислить по предыдущему как:
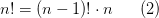
Введя обозначение 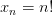 , получим соотношение:
, получим соотношение:
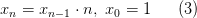
Вектора 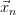 из формулы (1) можно интерпретировать как наборы значений переменных. Тогда вычисление требуемого элемента последовательности будет состоять в повторяющемся обновлении их значений. В частности для факториала:
из формулы (1) можно интерпретировать как наборы значений переменных. Тогда вычисление требуемого элемента последовательности будет состоять в повторяющемся обновлении их значений. В частности для факториала:
| x := 1; for i := 2 to n do x := x * i; writeln(x); |
Каждое такое обновление (x := x * i) называется итерацией, а процесс повторения итераций – итерированием.
Обратим, однако, внимание, что соотношение (1) является чисто рекурсивным определением последовательности и вычисление n-го элемента есть на самом деле многократное взятие функции f от самой себя:
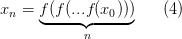
В частности для факториала можно написать:
| function Factorial(n: integer): integer; begin if n > 1 then Factorial := n * Factorial(n-1) else Factorial := 1; end; |
Следует понимать, что вызов функций влечет за собой некоторые дополнительные накладные расходы, поэтому первый вариант вычисления факториала будет несколько более быстрым. Вообще итерационные решения работают быстрее рекурсивных.
Прежде чем переходить к ситуациям, когда рекурсия полезна, обратим внимание еще на один пример, где ее использовать не следует.
Рассмотрим частный случай рекуррентных соотношений, когда следующее значение в последовательности зависит не от одного, а сразу от нескольких предыдущих значений. Примером может служить известная последовательность Фибоначчи, в которой каждый следующий элемент есть сумма двух предыдущих:
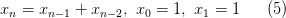
При «лобовом» подходе можно написать:
| function Fib(n: integer): integer; begin if n > 1 then Fib := Fib(n-1) + Fib(n-2) else Fib := 1; end; |
Каждый вызов Fib создает сразу две копии себя, каждая из копий – еще две и т.д. Количество операций растет с номером n экспоненциально, хотя при итерационном решении достаточно линейного по n количества операций.
На самом деле, приведенный пример учит нас не КОГДА рекурсию не следует использовать, а тому КАК ее не следует использовать. В конце концов, если существует быстрое итерационное (на базе циклов) решение, то тот же цикл можно реализовать с помощью рекурсивной процедуры или функции. Например:
| // x1, x2 – начальные условия (1, 1) // n – номер требуемого числа Фибоначчи function Fib(x1, x2, n: integer): integer; var x3: integer; begin if n > 1 then begin x3 := x2 + x1; x1 := x2; x2 := x3; Fib := Fib(x1, x2, n-1); end else Fib := x2; end; |
И все же итерационные решения предпочтительны. Спрашивается, когда же в таком случае, следует пользоваться рекурсией?
Любые рекурсивные процедуры и функции, содержащие всего один рекурсивный вызов самих себя, легко заменяются итерационными циклами. Чтобы получить что-то, не имеющее простого нерекурсивного аналога, следует обратиться к процедурам и функциям, вызывающим себя два и более раз. В этом случае множество вызываемых процедур образует уже не цепочку, как на рис. 1, а целое дерево. Существуют широкие классы задач, когда вычислительный процесс должен быть организован именно таким образом. Как раз для них рекурсия будет наиболее простым и естественным способом решения.
Деревья
Теоретической базой для рекурсивных функций, вызывающих себя более одного раза, служит раздел дискретной математики, изучающий деревья.
Дата добавления: 2016-07-05; просмотров: 4130;











