Разряд конденсатора на резистор
Рассмотрим переходный процесс при коротком замыкании в цепи с конденсатором и резистором (рис. 11.1), если предварительно конденсатор был заряжен до напряжения
Uc(0+) = U0 = E.
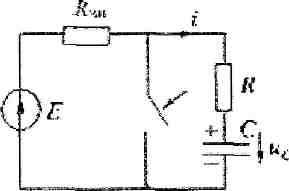
Рис.11.1.
Установившийся ток через конденсатор и установившееся напряжение на конденсаторе равны нулю. Для построения характеристического уравнения запишем по второму закону Кирхгофа уравнение для вновь образованного контура
Ri + uC = 0.
При расчете переходных процессов в цепях с конденсатором часто удобнее отыскать
сначала не ток, а напряжение на конденсаторе uC , а затем учитывая, что 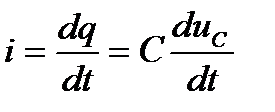 ,
,
найти ток через конденсатор. Поэтому запишем уравнение по второму закону Кирхгофа в виде:
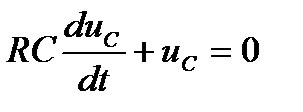
Характеристическое уравнение имеет вид:
RCp +1=0.
Общее решение для свободной составляющей напряжения:
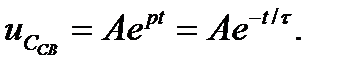
где A = U0 – постоянная интегрирования;
p = - 1/(RC) – корень характеристического уравнения
τ = RC – постоянная времени цепи.
С учетом нулевого значения установившегося напряжения получим напряжение на конденсаторе:
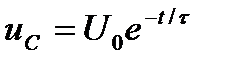 .
.
Переходный ток в цепи
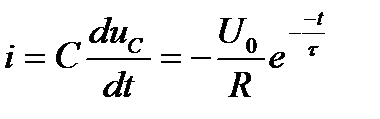
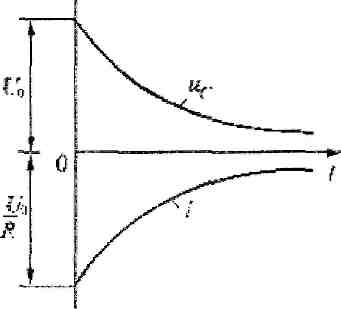
Рис. 11.2.
Кривые изменения напряжения на конденсаторе и тока в цепи во времени имеют вид экспонент (рис. 11.2.).
С энергетической точки зрения переходный процесс характеризуется переходом энергии электрического поля конденсатора в тепловую энергию в резисторе. Следует отметить; что сопротивление резистора влияет не на количество выделенной теплоты, а на начальное значение тока и длительность разряда. В самом деле
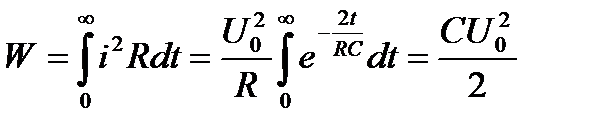
Дата добавления: 2016-07-05; просмотров: 2481;











